强化学习 CNN几个重要的基本概念与DQN
前言
最近在读一篇强化学习的论文以及代码,学到了很多新东西,特此记录下来。
CNN基本知识
Convolution:卷积
卷积核大小(filter size)为m * m卷积核(convolution kernel/convolution filter)一次移动一个卷积步长(convolution stride),在n * n图像上从左至右自上而下依次将卷积操作进行下去,最终输出大小(n-m+1)*(n-m+1)的卷积特征,同时该结果将作为下一层操作的输入。
Channels: 通道
首先,是 tensorflow 中给出的,对于输入样本中 channels 的含义。一般的RGB图片,channels 数量是 3 (红、绿、蓝);而monochrome图片,channels 数量是 1 。
Number of color channels in the example images. For color images, the number of channels is 3 (red, green, blue). For monochrome images, there is just 1 channel (black). ——tensorflow
其次,mxnet 中提到的,一般 channels 的含义是,每个卷积层中卷积核的数量。
- channels (int) : The dimensionality of the output space, i.e. the number of output channels (filters) in the convolution. ——mxnet*
个人觉得mxnet的说法比较容易理解,因为大部分时候并不会按照颜色来分通道。
Filter size:卷积核大小
卷积操作的两个超参数(hyper parameters)之一。
Stride:卷积步长
卷积操作的两个超参数之一。
Pooling:池化/汇合
平均值(最大值) 汇合在每次操作时,将汇合核覆盖区域中所有值的平均值(最大值)作为汇合结果。
Fully Connected Layer:全连接层
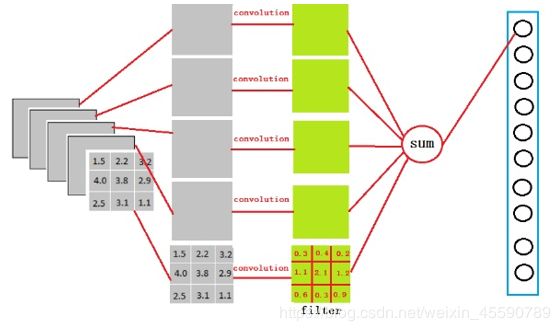
例如输入为 3 × 3 × 5 的特征张量,从上图我们可以看出,我们用一个3 x 3 x 5的filter 去卷积激活函数的输出,得到的结果就是一个fully connected layer 的一个神经元的输出,这个输出就是一个值。若后层是含4096个神经元的全连接层时,则可用卷积核为 3 × 3 × 5 × 4096 的全局卷积(4096个大小为3 * 3 * 5不同的卷积核分别对输入进行卷积,每一个输出都作为一个结果神经元)来实现这一全连接运算过程。
参数为filter_size = 3; padding = 0; stride = 1; D_in = 5; D_out = 4096。
Batch/Epoch
批大小,就是每次调整参数前所选取的样本(称为mini-batch或batch)数量:
如果批大小为N,每次会选取N个样本,分别代入网络,算出它们分别对应的参数调整值,然后将所有调整值取平均,作为最后的调整值,以此调整网络的参数。
如果批大小N很大,例如和全部样本的个数一样,那么可保证得到的调整值很稳定,是最能让全体样本受益的改变。
如果批大小N较小,例如为1,那么得到的调整值有一定的随机性,因为对于某个样本最有效的调整,对于另一个样本不一定最有效(就像对于识别某张黑猫图像最有效的调整,不一定对于识别另一张白猫图像最有效)
训练中的另一个重要概念是epoch。每学一遍数据集,就称为1个epoch。 举例,若数据集中有1000个样本,批大小为10,那么将全部样本训练1遍后,网络会被调整1000/10=100次。但这并不意味着网络已达到最优,我们可重复这个过程,让网络再学1遍、2遍、3遍数据集。
注意每一个epoch都需打乱数据的顺序,以使网络受到的调整更具有多样性。同时,我们会不断监督网络的训练效果。通常情况下,网络的性能提高速度会越来越慢,在几十到几百个epoch后网络的性能会趋于稳定,即性能基本不再提高。
DQN(Deep Q Network)
建议阅读:
NIPS2013 Playing Atari with Deep Reinforcement Learning
Nature-2015:Human-level control through deep reinforcement learning
建议观看:https://morvanzhou.github.io/tutorials/machine-learning/reinforcement-learning/2-1-A-q-learning/
本篇博文主要想记的就是自己对DQN这个算法的理解。一开始看这篇paper的时候结合GitHub上一个强化学习玩Flappy Bird的代码觉得自己懂了这个算法,但是后来在读另一篇关于DDPG的paper时确被DQN结合Actor-Critic绕晕了,可见并没完全吃透。
Q-learning算法
DQN是基于Q-learning的。Q-Learning是强化学习算法中value-based的算法,Q即为Q(s,a)就是在某一时刻的 s 状态下(s∈S),采取 动作a (a∈A)动作能够获得收益的期望,环境会根据agent的动作反馈相应的回报reward r,所以算法的主要思想就是将State与Action构建成一张Q-table来存储Q值,然后根据Q值来选取能够获得最大的收益的动作。
即agent通过每次选取当前最优动作来不断玩游戏、不断更新Q-table(我理解为策略表),自学习到更优。
由Bellman方程求解马尔可夫决策过程,总结出更新公式: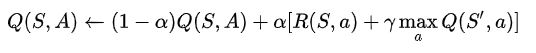
还有一种说法,和上面的公式是等价的:

两个是一样的。
Deep Q Network
记忆库
记忆库就是一个样本集。每一个样本包含当前状态,当前状态做出的动作,做出动作的奖励以及下一个状态。每完成一个动作后,CNN并不直接学习当前的数据,而是存到记忆库中,从记忆库中随机抽一个出来学习。这样可以切断数据间的相关性。
CNN算Q
用CNN计算S对应的Q值。用CNN算Q值不难理解,比较妙的是用算出来的Q值当作Q网络更新的学习目标。Q-learning那样学习是线性的,而这样不是。
Nature Deep Q Network
Q-Target和Q
这个改进版最妙的是用了两个网络。简单来说,Q是由S决定动作A的网络,但这个网络需要学习集,Q-target就是用来算学习集/目标数据的。
上述的做法会令算Q-target的网络更新慢(因为只更新Q没更新Q-target),也可以看作Q-target参数被冻结了。所以每隔一段时间,会把比较新的网络(Q)copy到比较老的网络(Q-target),“解冻”。
后记
后续改进的DDQN以及Actor-Critic什么的有时间再写吧。本篇记载了DQN的基本最重要的思路,用这些跑个Flappy Birds啥的还是很OK的。

