毕业实用模型(三)——时间序列forecast包的使用
目录
- 00引言
- 1、accuracy函数
- 2、Acf、Pacf、taperedacf、taperedpacf
- 3、arfima
- 4、Arima函数
- 5、arima.errors函数
- 6、arimaorder
- 7、auto.arima
- 8、ggplot2中的时间序列相关系数
- 9、tslm
- 10、CV交叉验证
- 11、forecast
- 12、geom_forecast
- 13、总结
- 14、参考文献
00引言
在毕业实用统计模型(一)——时间序列1中介绍了时间序列的模型的基本建模思路,在毕业设计实用模型(二)——时间序列之SARIMA2中说明了ARMA、ARIMA、SARIMA三大模型的关系与参数调整。但是在实际建模中往往会遇到更加实际的需求:模型的评估、参数检验、预测图的展示、模型参数的调整。对于很对不喜欢编程的人来说很是痛苦。本文将会重点从上述几个方面讲述forecast包里的主要的函数,并给出实例。从本文中你将会学会:
- 更加高效的的模型预测图。
- 模型的参数检验
- 模型定阶的函数
- 模型的评估函数
- 拟合线性的模型函数
- 相关图绘画,以及误差的标注
- 输出模型的预测误差
注:本文部分代码案例来自
forecast包,大家有疑问可以自行去查找3.如果进不去可以运行下面代码会找到。
library(forecast)
help(package = forecast)
1、accuracy函数
描述:输入参数是模型,输出下面的结果:
| 参数 | 含义 |
|---|---|
| ME: | 平均误差 |
| RMSE | 根均方误差 |
| MAE | 平均绝对误差 |
| MPE | 平均百分比误差 |
| MAPE | 平均绝对百分比误差 |
| MASE | 平均绝对比例误差 |
| ACF1 | 滞后1阶误差的自相关 |
函数示例:
> n = 50;p = 10
> x = rnorm(p)
> fit1 <- ar(rnorm(n))
> fit <- forecast(fit1, h = p)
> accuracy(fit)
ME RMSE MAE MPE MAPE MASE
Training set 0.1143757 1.594933 1.33946 287.3696 602.0162 1.299599
ACF1
Training set -0.1573861
> accuracy(fit,x = x)
ME RMSE MAE MPE MAPE MASE
Training set 0.1143757 1.594933 1.3394599 287.3696 602.0162 1.2995990
Test set -0.2194929 0.833041 0.6356776 132.4545 239.1639 0.6167606
ACF1
Training set -0.1573861
Test set NA
> plot(fit)
> lines(51:60,x)
2、Acf、Pacf、taperedacf、taperedpacf
这四个函数分别是自相关函数、偏自相关函数、带有误差的自相关函数、带有误差的偏自相关函数。前两个很熟悉和内置的acf、pacf一样,下面只给出后两个的示例:
n = 50
set.seed(0)
x = rnorm(n, 1,3)
taperedacf(x, nsim=50)
taperedpacf(x, nsim=50)
3、arfima
可以建立长期记忆的时间序列模型。
直接给例子了哦:
> n = 50 # 生成数据
> set.seed(0)
> x = rnorm(n, 1,3)
> fit <- arfima(x) # 拟合模型
输出模型效果:
> fit
> Call:
arfima(y = x)
Coefficients:
d
0.06385553
sigma[eps] = 2.716399
a list with components:
[1] "log.likelihood" "n" "msg" "d"
[5] "ar" "ma" "covariance.dpq" "fnormMin"
[9] "sigma" "stderror.dpq" "correlation.dpq" "h"
[13] "d.tol" "M" "hessian.dpq" "length.w"
[17] "residuals" "fitted" "call" "x"
[21] "series"
> summary(fit)
Call:
arfima(y = x)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
d 6.386e-02 1.278e-06 49958 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
sigma[eps] = 2.716399
[d.tol = 0.0001221, M = 100, h = 1.285e-06]
Log likelihood: -120.9 ==> AIC = 245.844 [2 deg.freedom]
画出残差信息:
tsdisplay(residuals(fit))
4、Arima函数
函数介绍:这个函数可以拟合平稳或者非平稳的且已经知道参数的时间序列模型。也可以带有季节因素。
n = 50
set.seed(0)
x = rnorm(n, 1,3) # 生成数据
library(ggplot2) # 载入画图包
x %>%
Arima(order=c(3,1,1)) %>%
forecast(h=5) %>%
autoplot
上述代码用了管道函数,ggplot2包。对模型从数据到预测到建模一部到位。给大家看看Arima的参数。
function (y, order = c(0, 0, 0), seasonal = c(0, 0, 0), xreg = NULL,
include.mean = TRUE, include.drift = FALSE, include.constant,
lambda = model$lambda, biasadj = FALSE, method = c("CSS-ML",
"ML", "CSS"), model = NULL, x = y, ...)
5、arima.errors函数
该函数使用简单,用于输出模型预测每一期的误差。注意和residuals函数进行区分。
# 生成数据建模
n = 50
set.seed(0)
x = rnorm(n, 1,3)
fit <- arfima(x)
# 计算结果
> arima.errors(fit) # 预测误差
Deprecated, use residuals.Arima(object, type='regression') instead
Time Series:
Start = 1
End = 50
Frequency = 1
[1] 4.78886285 0.02129992 4.98939779 4.81728796 2.24392430 -3.61985013
[7] -1.78570110 0.11583866 0.98269848 8.21396017 3.29078038 -1.39702775
[13] -2.44297103 0.13161528 0.10235465 -0.23453250 1.75667034 -1.67576338
[19] 2.30704990 -2.71261527 0.32719634 2.13218694 1.40000908 3.41256853
[25] 0.82867968 2.51082392 4.25730809 -1.07286152 -2.85379806 1.14017852
[31] 0.29288033 -0.62866477 -0.29993095 -0.94841494 3.18025224 4.45573526
[37] 3.97648110 -0.28853933 4.71491230 0.16196115 6.27370927 2.68223827
[43] -0.35835192 -1.49612989 -2.49971164 -2.19677174 -3.69134615 4.46961099
[49] 3.49614139 0.31801393
> residuals(fit) # 残差
Time Series:
Start = 1
End = 50
Frequency = 1
[1] 3.71706994 -1.28784846 3.87358515 3.45503095 0.78349981 -4.98056775
[7] -2.74303846 -0.77184435 0.03669199 7.20508533 1.79698739 -2.80377609
[13] -3.54880551 -0.77827016 -0.86325716 -1.20139553 0.81773766 -2.72392791
[19] 1.43279254 -3.76501026 -0.47528735 1.24438107 0.37471968 2.37151650
[25] -0.35743144 1.41677218 3.08432283 -2.39421040 -3.91173996 0.30272726
[31] -0.68356344 -1.59285606 -1.19943417 -1.83611913 2.34677217 3.38917930
[37] 2.72730075 -1.60715574 3.61473632 -1.17228009 5.12889059 1.21871171
[43] -1.73495615 -2.66242875 -3.50034594 -3.04300026 -4.46595111 3.84607121
[49] 2.44020165 -0.85475604
6、arimaorder
函数功能:输出函数的阶数,用于时间序列的自动定阶。下面用自动定阶函数auto.arima和管道函数结合输出参数。给出示例。
n = 50
set.seed(100)
x = rnorm(n, 3, 5) + 1:50 # 生成数据
x %>% auto.arima %>% arimaorder
p d q
3 1 0
可以配合arima函数进行模型的参数的确定。
7、auto.arima
函数功能:可以使用函数进行自动定阶。下面时该函数的参数。这里会进行讲解并给出具体的实例:
auto.arima(
y, # 数据
d = NA, # 原始数据差分的阶数
D = NA, # 季节因素的差分阶数
max.p = 5, # 遍历达到的最大的AR模型的阶数。
max.q = 5, # 遍历达到的最大的MA模型的阶数。
max.P = 2, # 季节因素遍历达到的最大的AR模型的阶数。
max.Q = 2, # 季节因素遍历达到的最大的MA模型的阶数。
max.order = 5,
max.d = 2,
max.D = 1,
start.p = 2, # 开始遍历的AR模型的阶数。
start.q = 2, # 开始遍历的MA模型的阶数。
start.P = 1,
start.Q = 1,
stationary = FALSE, #
seasonal = TRUE,
ic = c("aicc", "aic", "bic"), # 常用的选择模型的标准
stepwise = TRUE,
nmodels = 94,
trace = FALSE,# 是否跟踪模型的选择
approximation = (length(x) > 150 | frequency(x) > 12),
method = NULL,
truncate = NULL,
xreg = NULL,
test = c("kpss", "adf", "pp"), # 平稳性检验的方式
test.args = list(),
seasonal.test = c("seas", "ocsb", "hegy", "ch"), # 季节性分析
seasonal.test.args = list(),
allowdrift = TRUE, # 可以去掉漂移项
allowmean = TRUE, # 可以去掉均值项
lambda = NULL,
biasadj = FALSE,
parallel = FALSE,
num.cores = 2,
x = y,
...
)
auto.arima函数的参数众多,我把上述函数的参数给了一定的备注。大家可以根据这个注释和数据的其他的检验依据自己去逐一的验证调试。最终得出一个比较满意的模型。
下面给出部分调参的实例:
# 生成数据
n = 50
set.seed(100)
x = rnorm(n, 3, 5) + 1:50
下面画时序图,看看数据效果
# 画时序图
plot(ts(x))
# 参数调优
> auto.arima(x) # 直接建模
Series: x
ARIMA(1,1,0) with drift
Coefficients:
ar1 drift
-0.7383 0.9139
s.e. 0.0960 0.3643
sigma^2 estimated as 20.13: log likelihood=-142.45
AIC=290.9 AICc=291.43 BIC=296.58
> auto.arima(x, allowdrift = F) # 去掉模型漂移
Series: x
ARIMA(1,1,0)
Coefficients:
ar1
-0.7016
s.e. 0.1012
sigma^2 estimated as 22.23: log likelihood=-145.35
AIC=294.69 AICc=294.95 BIC=298.47
> auto.arima(x, d = 1) # 设置差分阶数,为了防止模型的过差分可以设置这个参数。
Series: x
ARIMA(1,1,0) with drift
Coefficients:
ar1 drift
-0.7383 0.9139
s.e. 0.0960 0.3643
sigma^2 estimated as 20.13: log likelihood=-142.45
AIC=290.9 AICc=291.43 BIC=296.58
> auto.arima(x, d = 1, allowdrift = F)
Series: x
ARIMA(1,1,0)
Coefficients:
ar1
-0.7016
s.e. 0.1012
sigma^2 estimated as 22.23: log likelihood=-145.35
AIC=294.69 AICc=294.95 BIC=298.47
下面展示追踪模型的参数:
> auto.arima(x, d = 2, trace = T)
ARIMA(2,2,2) : Inf
ARIMA(0,2,0) : 377.2692
ARIMA(1,2,0) : 313.2075
ARIMA(0,2,1) : Inf
ARIMA(2,2,0) : 308.1753
ARIMA(3,2,0) : 304.7953
ARIMA(4,2,0) : 306.6614
ARIMA(3,2,1) : Inf
ARIMA(2,2,1) : Inf
ARIMA(4,2,1) : Inf
Best model: ARIMA(3,2,0)
Series: x
ARIMA(3,2,0)
Coefficients:
ar1 ar2 ar3
-1.3557 -0.8481 -0.3615
s.e. 0.1449 0.2217 0.1445
sigma^2 estimated as 28.41: log likelihood=-147.93
AIC=303.87 AICc=304.8 BIC=311.35
更改准则AICc成AIC继续追踪模型的参数:
> auto.arima(x, d = 2, ic = "aic", trace = T)
ARIMA(2,2,2) : Inf
ARIMA(0,2,0) : 377.1822
ARIMA(1,2,0) : 312.9408
ARIMA(0,2,1) : Inf
ARIMA(2,2,0) : 307.6298
ARIMA(3,2,0) : 303.865
ARIMA(4,2,0) : 305.2329
ARIMA(3,2,1) : Inf
ARIMA(2,2,1) : Inf
ARIMA(4,2,1) : Inf
Best model: ARIMA(3,2,0)
Series: x
ARIMA(3,2,0)
Coefficients:
ar1 ar2 ar3
-1.3557 -0.8481 -0.3615
s.e. 0.1449 0.2217 0.1445
sigma^2 estimated as 28.41: log likelihood=-147.93
AIC=303.87 AICc=304.8 BIC=311.35
这个函数的参数就介绍到这里,大家用到自己继续探索。
8、ggplot2中的时间序列相关系数
这里把函数内置的实例给出来。
# 载入画图的ggplot2包
library(ggplot2)
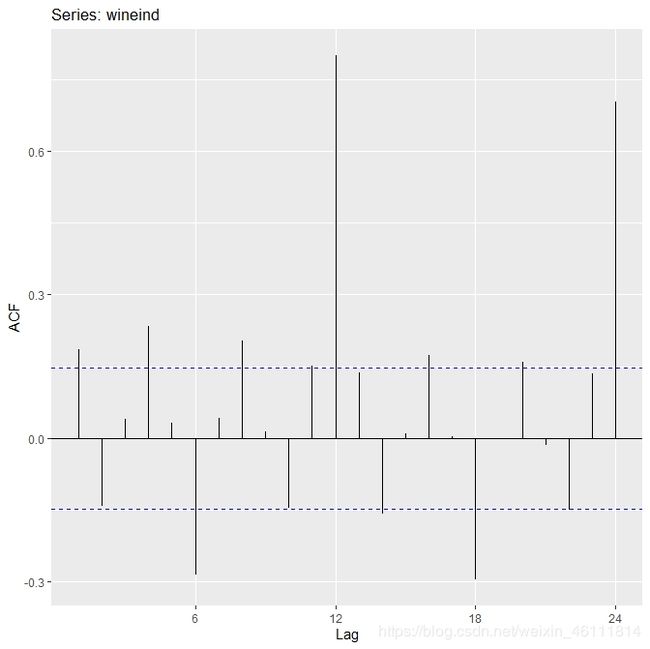
下面的例子使用winneind数据。是个时间序列数据。
ggAcf(wineind)
wineind %>% taperedacf(plot=FALSE) %>% autoplot
ggCcf(mdeaths, fdeaths)
9、tslm
函数功能:用时间序列分量拟合线性模型
为了我方便第一次见到的同学学习,先贴出模型的参数:
> tslm
function (formula, data, subset, lambda = NULL, biasadj = FALSE,
...)
formula参数是公式、data是数据。下面使用函数例子展示函数功能。
> y <- ts(rnorm(120,0,3) + 20*sin(2*pi*(1:120)/12), frequency=12) # 构造数据
> fit1 <- tslm(y ~ trend + season) # 趋势+季节
> fit1
Call:
tslm(formula = y ~ trend + season)
Coefficients:
(Intercept) trend season2 season3 season4
10.20906 0.01175 7.31274 8.82928 7.04245
season5 season6 season7 season8 season9
-2.04022 -10.24111 -20.57768 -27.61414 -30.16768
season10 season11 season12
-27.56840 -21.53062 -10.35272
plot(forecast(fit1, h=20)) # 画出模型1的预测图
> fit2 <- tslm(y ~ season)
> fit2
Call:
tslm(formula = y ~ season)
Coefficients:
(Intercept) season2 season3 season4 season5
10.856 7.324 8.853 7.078 -1.993
season6 season7 season8 season9 season10
-10.182 -20.507 -27.532 -30.074 -27.463
season11 season12
-21.413 -10.223
plot(forecast(fit2, h=20)) # 画出模型2的预测图
10、CV交叉验证
CV函数显示模型的CV AIC AICc BIC AdjR2值,用上述模型直接给出例子。
> CV(fit1)
CV AIC AICc BIC AdjR2
12.851627 306.718526 310.718526 345.743411 0.945285
> CV(fit2)
CV AIC AICc BIC AdjR2
12.7985986 306.6337582 310.0677205 342.8711509 0.9449195
11、forecast
这个函数可以给出模型的预测值用于画图和分析。
下面给出上述模型一的预测值。
> forecast(fit1, h=20) # 往后预测20期
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 11 11.631361 6.993384 16.269339 4.501348 18.761374
Feb 11 18.955852 14.317875 23.593829 11.825839 26.085865
Mar 11 20.484149 15.846172 25.122127 13.354136 27.614162
Apr 11 18.709071 14.071094 23.347048 11.579058 25.839084
May 11 9.638164 5.000187 14.276141 2.508151 16.768177
Jun 11 1.449025 -3.188953 6.087002 -5.680989 8.579038
Jul 11 -8.875796 -13.513773 -4.237818 -16.005809 -1.745783
Aug 11 -15.900500 -20.538478 -11.262523 -23.030513 -8.770487
Sep 11 -18.442285 -23.080262 -13.804307 -25.572298 -11.312272
Oct 11 -15.831247 -20.469224 -11.193269 -22.961260 -8.701233
Nov 11 -9.781716 -14.419693 -5.143739 -16.911729 -2.651703
Dec 11 1.407943 -3.230034 6.045921 -5.722070 8.537957
Jan 12 11.772416 7.109642 16.435190 4.604282 18.940549
Feb 12 19.096906 14.434132 23.759680 11.928773 26.265039
Mar 12 20.625203 15.962429 25.287977 13.457070 27.793337
Apr 12 18.850125 14.187351 23.512899 11.681992 26.018259
May 12 9.779218 5.116444 14.441992 2.611085 16.947351
Jun 12 1.590079 -3.072695 6.252853 -5.578054 8.758212
Jul 12 -8.734741 -13.397516 -4.071967 -15.902875 -1.566608
Aug 12 -15.759446 -20.422220 -11.096672 -22.927579 -8.591313
结果说明:第一列是时间、第二列是预测值、后面4列是预测值的80%、95%的置信下限和置信下限。
12、geom_forecast
这个图是ggplot2的预测图,下面贴出代码给出效果。这个函数也需要结合ggplot2包进行。
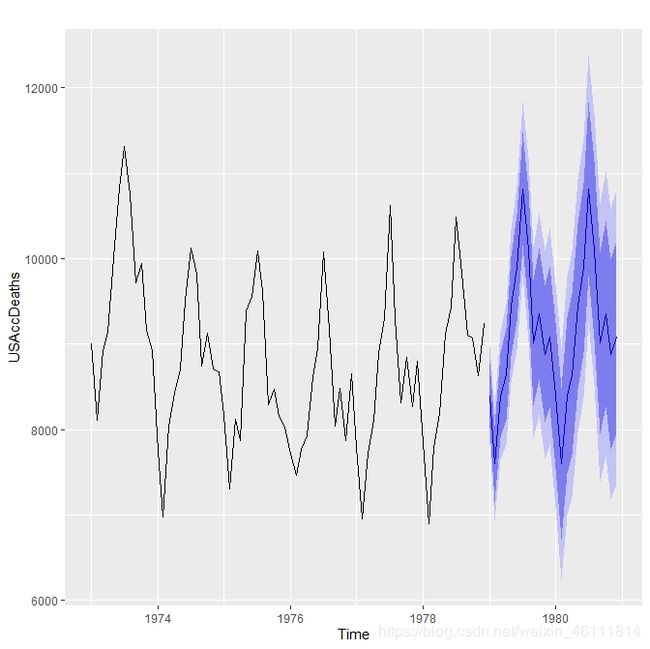
library(ggplot2)
autoplot(USAccDeaths) + geom_forecast() # 图一
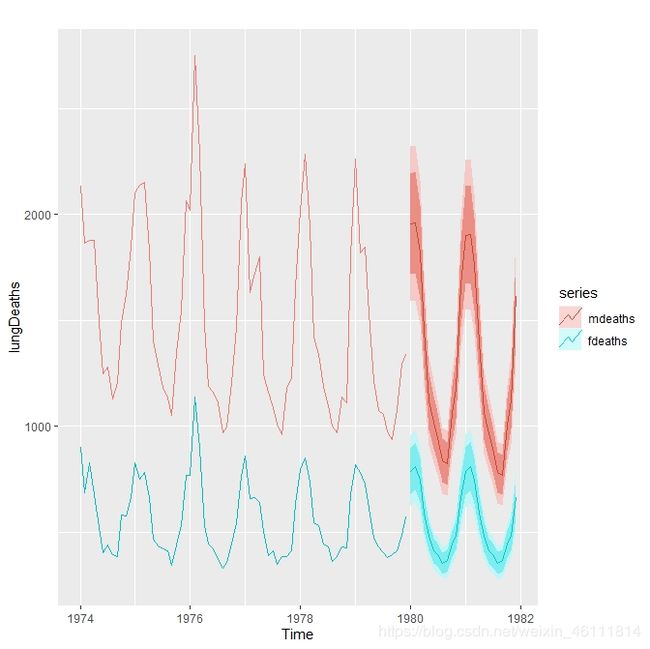
lungDeaths <- cbind(mdeaths, fdeaths)
autoplot(lungDeaths) + geom_forecast() # 图二
13、总结
forecast包里的函数众多,上面只是介绍很少的一部分,更多函数的使用方式留着给大家探索。
14、参考文献
https://blog.csdn.net/weixin_46111814/article/details/105348265 ↩︎
https://blog.csdn.net/weixin_46111814/article/details/105370507 ↩︎
http://127.0.0.1:17627/library/forecast/html/00Index.html ↩︎