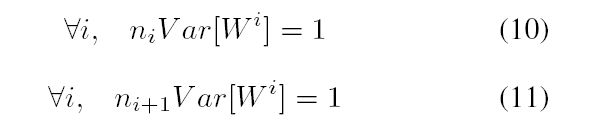理解训练深层前馈神经网络的难度（Undetanding the difficulty of training deep feedforward neural networks ）...

译者按：大神bengio 的经典论文之一，不多说

作者：Xavier Glorot Yoshua Bengio     加拿大魁北克  蒙特利尔大学

 

摘要：在2006年以前，似乎深度多层的神经网络没有被成功训练过。自那以后少数几种算法显示成功地训练了它们，实验结果表明了深度多层的架构的优越性。所有这些实验结果都是通过新的初始化或训练机制获得的。我们的目标是更好地理解为什么随机初始化的标准梯度下降法在深度神经网络下表现如此糟糕，为了更好地理解最近的相对成功并帮助设计未来更好的算法。我们首先观察了非线性激活函数的影响。我们发现logistic sigmoid激活不适用于随机初始化的深度网络，因为它的平均值，特别是顶部隐藏层进入饱和状态。令人惊讶的是，我们发现饱和单位可以移出自我饱和，尽管低，并且在训练神经网络时解释有时会出现高原。我们发现饱和度较低的新非线性通常是有益的。最后，我们研究层和训练过程中激活和梯度如何变化，当训练可能更加困难时，与每层相关联的雅可比矩阵的奇异值远不等于1。基于这些考虑，我们提出了一种新的初始化方案，其带来显着更快的收敛。

 

1  深度神经网络

深度学习方法的目标是通过低层次特征的组合形成更高层次的特征层次结构。它们包括用于各种深层架构的学习方法，包括具有许多隐藏层的神经网络（Vincentet al。，2008）和具有多层隐变量的图形模型（Hinton等，2006）等（Zhuet al。， 2009; Weston等，2008）。由于它们的理论吸引力，来自生物学和人类认知的灵感以及由于视觉的经验成功（Ranzato等人，2007; Larochelle等人，2007），因此他们最近注意到了它们（参见（Bengio，2009） 2007; Vincent等，2008）和自然语言处理（NLP）（Collobert＆Weston，2008; Mnih＆Hinton，2009） 的联系。Bengio（2009）回顾和讨论的理论结果表明，为了学习能够代表高级抽象的复杂功能（例如，在视觉，语言和其他AI级任务中），可能需要深层架构。最近的深层结构实验结果是通过模型得到的，这些模型可以转化为中间监督神经网络，但初始化方法不同于经典的前向神经网络（Rumelhart et al。，1986）。为什么这些新算法比标准随机初始化和基于梯度的无监督训练准则优化工作得更好？部分答案可能在最近对无监督预训练效果的分析中发现（Erhan等人，2009），表明它起着规范化的作用，在优化过程的“更好”盆地中初始化参数，对应于明显的局部但与早期的工作（Bengio等人，2007）相比，即使是纯粹的监督但贪婪的分层过程也会带来更好的结果。因此，在这里，我们不是专注于无监督的预培训或半监督标准给深层架构带来什么，而是专注于分析好的旧（但深度）多层神经网络可能出现的问题。我们的分析是由调查实验驱动到monitrogen激活（注意饱和我们还评估了这些激活函数选择（以及它可能影响饱和度的思想）和初始化过程（由于无监督预训练是一种特殊形式的初始化，并且它具有隐含单位） adrastic影响）。

2实验设置和数据集

生成本节介绍的新数据集的代码可从以下网址获得

http://www.iro.umontreal.ca/˜lisa/twiki/bin/view.cgi/Public/DeepGradientsAISTATS2010

2.1无限数据集的在线学习：

Shapeset-3×2

最近在深入架构下的工作（见Bengio（2009）图7）显示，即使在非常大的训练集或在线学习中，从无监督预训练初始化产生了实质性的改进，随着训练样例数量的增加，这种改进不会消失。在线设置也很有趣，因为它专注于优化问题而不是小样本正则化效果，所以我们决定在我们的实验中包含一个由Larochelle等人启发的合成图像数据集。 （2007）和Larochelle等人（2009年），从中可以抽取所需的许多实例，用于测试在线学习情景。

 

 

图1：顶部：64×64分辨率的Shapeset-3×2图像。 我们使用的例子是32×32分辨率。 学习者试图预测哪些对象（平行四边形，三角形或椭圆形）存在，并且可以存在1或2个对象，从而产生9种可能的分类。 底部：全分辨率的Small-ImageNet图像。

我们将这个数据集称为Shapeset-3×2数据集，图1中的示例图像（顶部）。 Shapeset-3×2包含1或2个二维物体的图像，每个物体取自3个形状类别（三角形，平行四边形，椭圆形），并放置有随机形状参数（相对长度和/或角度），缩放，旋转，平移和灰度。

我们注意到，图像中只有一个形状，识别它的任务太简单了。因此，我们决定对两个物体的图像进行取样，限制第二个物体与第一个物体不超过其面积的百分之五十，以避免完全隐藏它。

任务是预测存在的物体（例如三角形+椭圆，平行四边形+平行四边形，单独三角形等），而不必区分前景形状和背景形状。这因此定义了九个配置类。

该任务相当困难，因为我们需要发现旋转，平移，缩放，对象颜色，遮挡和形状的相对位置等方面的不变性。同时，我们需要提取预测哪些物体形状存在的可变性因素。

图像的大小是任意的，但我们将其固定为32×32，以便有效地处理高密度网络。

2.2有限数据集

MNIST数字（LeCun等人，1998a）数据集有50,000个训练图像，10,000个验证图像（用于超参数选择）和10,000个测试图像，每个图像显示10个像素之一的28×28灰度像素图像数字。 CIFAR-10（Krizhevsky＆Hinton，2009）是微型图像数据集的标记子集，其中包含50,000个训练样例（我们从中提取10,000个作为验证数据）和10,000个测试样例。每个图像中对应于主要对象的有10个类别：飞机，汽车，鸟，猫，鹿，狗，青蛙，马，船或卡车。这些课程是平衡的。每个图像都是彩色的，但尺寸仅为32×32像素，因此输入是32×32×3 = 3072个实际值的向量。 Small-ImageNet，它是一套微小的37×37灰度级图像数据集，由http://www.image-net.org上的高分辨率和更大集合计算得出，带有来自WordNet名词层次结构的标签。我们已经使用了90,000个示例进行培训，10,000个用于验证组，10,000个用于测试。有10个平衡类：爬行动物，车辆，鸟类，哺乳动物，鱼类，家具，仪器，工具，鲜花和水果图1（底部）显示随机选择的例子。

2.3实验设置

我们优化了具有一至五层隐藏层的前馈神经网络，每层有一千个隐藏单元，并对输出层进行了softmax逻辑回归。成本函数是负对数似然-log P（y | x），其中（x，y）是（输入图像，目标类）对。神经网络在10个小批量的随机反向传播上进行了优化，即@ -log P（y | x）训练对（x，y）的平均g并用于更新参数？在那个方向，与？ ？ - ？g。学习率？是在大量更新（500万）后基于验证集错误进行优化的超参数。我们改变了隐藏层中非线性激活函数的类型：sigmoid 1 /（1 + e-x），双曲正切tanh（x）和一个新提出的激活函数（Bergstra等人，2009年） softsign，x /（1 + | x |）。软标志类似于双曲正切（它的范围是-1到1），但它的尾部是二次多项式而不是指数，即它接近它的渐近线要慢得多。在比较中，我们分别为每个模型搜索最佳超参数（学习速率和深度）。请注意，Shapeset-3×2的最佳深度总是5，除了S形，它是四个。我们使用以下常用启发式将偏差初始化为0和各层的权重Wij：

3 激活功能的影响与训练期间的饱和度

我们想要避免的两件事情可以从中揭示出来,激活的演变是过度饱和的. 激活功能一方面（然后梯度不会传播）以及过于线性的单位（他们不会计算

有趣的事情）。

3.1 Sigmoid实验

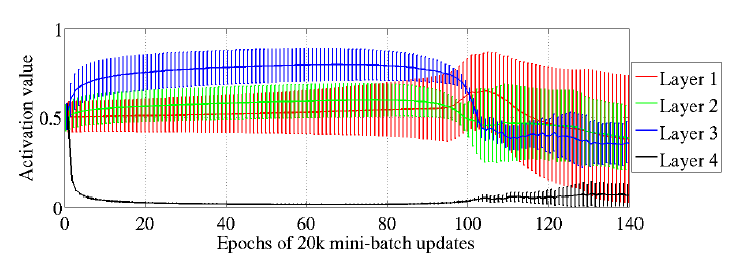
Sigmoid非线性已经被证明可以减慢学习，因为它的非零均值在Hessian中引入了重要的奇异值（LeCun et al。，1998b）。在本节中，我们将看到由于深度前馈网络中的激活功能导致的另一个症状行为。我们希望通过查看训练过程中激活的演变来研究可能的饱和度，本节中的数字显示了Shapeset-3×2数据的结果，但在其他数据集中观察到类似的行为。图2显示了在用S形激活函数训练深层结构期间，每个隐藏层激活值（在非线性之后）的演变。第1层是指第一个隐藏层的输出，并且有四个隐藏层。该图显示了这些激活的平均值和标准偏差。这些统计数据和直方图是在学习期间的不同时间计算的，通过查看300个固定测试示例的激活值。

 

 

图2：平均值和标准偏差（垂直线）在监督期间激活值（sigmoid的输出）学习，为深层建筑的不同隐藏层。顶部隐藏层快速饱和为0（减速放下所有的学习），但是然后缓慢地去饱和时代100。

我们看到在开始时非常快速地，最后一个隐藏层的所有S形激活值被推到其较低的饱和度值0.相反，其他层的平均激活值大于0.5，并且随着我们从 输出层到输入层, 我们发现这种饱和在具有S形激活的更深网络中可以持续很长时间. 例如，在训练期间，深度模型从未逃脱这种制度。 令人惊讶的是，对于中间数量的隐藏层（这里是四层），饱和状态可能会逃脱。 在顶层隐藏层移出饱和的同时，第一个隐藏层开始饱和并因此趋于稳定。

我们假设这种行为是由于随机初始化和隐藏单元输出为0对应于饱和S形的事实相结合。注意，具有S形但是从无监督预训练（例如从RBM）初始化的深网络不会受到这种饱和行为的影响。我们提出的解释依赖于这样一个假设：随机初始化网络的低层计算最初对分类任务没有用处，与从无监督预训练获得的变换不同。逻辑层输出softmax（b + Wh）最初可能更多地依赖于它的偏差b（其被快速学习）而不是依赖于从输入图像导出的最高隐藏激活h . 因为h将以不能预测y ，可能主要与x的其他可能更主要的变化相关。因此，误差梯度倾向于将Wh推向0，这可以通过将h推向0来实现。在对称激活函数（如双曲线正切和软标志）的情况下，坐在0附近是好的，因为它允许梯度向后流动。然而，将S形输出推到0会使它们进入饱和状态，这将防止梯度向后流动，并防止较低层学习有用的特征。最终但是慢慢地，较低层向更有用的特征移动，并且顶端隐藏层然后移出饱和区域。但请注意，即使在此之后，网络也会转变为质量较差的解决方案（也就是泛化）那么发现具有对称激活功能的那些， 可以在图11中看到。

3.2双曲正切的实验

如上所述，双曲正切网络没有遭受顶级隐藏的那种饱和行为因为它的S形网络观察到的层对称度在0.左右。但是，用我们的标准重量

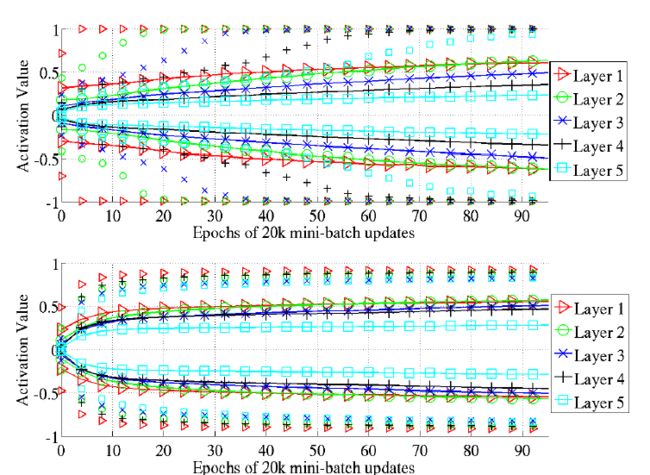
初始化，我们观察到一个连续发生饱和现象从第1层开始在网络中传播，如图3所示。为什么会发生这种情况仍有待了解。

 

 

图3：上图：98个百分点（仅标记）和标准偏差（带标记的实线）的分布中的双曲正切网络的激活值学习的过程。 我们看到第一个隐藏层饱和第一，然后是第二等。底部：98个百分点（单独标记）和标准偏差（实线与标记）为softsign的激活值分布学习期间。 这里不同的层饱和较少并一起做。

3.3 Softsign的实验

Softsign x /（1 + | x |）类似于双曲正切，但由于它的渐近线（多项式而不是指数），可能在饱和度方面表现不同。 我们在图3上看到饱和不会像双曲线正切那样发生在另一层之后。 它在开始时更快，然后缓慢，并且所有层一起朝着更大的权重移动。 我们还可以在训练结束时看到激活值的直方图与双曲线切线的直方图有很大不同（图4）。 而后者产生激活分布的模式主要在极端（渐近线-1和1）或大约0处，软标志网络在其膝盖周围具有激活模式（在0和-1之间的平坦状态和1）。 这些区域存在非常大的非线性，但梯度将流动良好。

 

 

图4：激活值归一化直方图在学习结束，平均在同一层单位和跨越300个测试示例。 顶部：激活函数是双曲线的切线，我们看到下层的重要饱和度。底部：激活功能是softsign，我们看到很多（-0.6，-0.8）和（0.6,0.8）附近的激活值单位不饱和，但是非线性。

 

4  梯度及其传播的 研究

4.1成本函数的影响

我们发现逻辑回归或条件对数似然成本函数（-log P（y | x）加上softmax输出）比传统上用于训练前馈神经网络的二次成本（分类问题）好得多 Rumelhart等，1986）。 这不是一个新的观察结果（Solla et al。，1988），但我们发现在这里强调这一点很重要。 我们发现训练准则中的平稳（作为参数的函数）较少出现在对数似然成本函数中。 我们可以在图5中看到这一点，该图将训练准则描绘为具有双曲正切单位的双层网络（一个隐藏层）以及随机输入和目标信号的两个权重的函数。 平均成本显然更严重。

4.2初始化时的梯度

4.2.1理论考虑和新的规范化初始化

我们研究反向传播的梯度，或等价的投影偏差在每一层的成本函数的梯度。 布拉德利（Bradley，2009）发现，在初始化之后，随着从输出层向输入层移动，反向传播梯度变小。 他研究了在每一层都具有线性激活的网络，发现随着我们在网络中倒退，反向传播梯度的方差减小。 我们也将从研究线性状态开始。

 

 

图5：交叉熵（黑色，顶部表面）和作为两个函数的二次（红色，底面）成本两层网络的权重（每层一个）W1分别在第一层上和W2在第二层上，输出层。

对于使用对称激活的稠密人工神经网络函数f的单位导数为0（即f0（0）= 1），如果我们为第i层的激活矢量写si和si层i的激活函数的参数向量，

我们有si = ziWi + bi和zi + 1 = f（si）。 从这些定义我们获得以下内容：

 

 

 

将根据输入，输出和权重初始化随机性来表示差异。 考虑这样的假设：我们在初始化时处于线性状态，权重独立初始化，输入特征方差相同（= V ar [x]）。 那么我们可以这样说，用ni表示第i层的大小，x表示网络输入，

 

 

 

我们为所有的共享标量方差写V ar [Wi0] 第i0层的权重。 然后，对于具有d层的网络，

 

 

 

从前向传播的角度来看，保持信息流动我们希望那样

 

 

 

从后向传播的角度来看，我们也是如此喜欢拥有

 

 

 

两个条件转换为

 

 

 

作为这两种限制之间的折衷，我们可能会这样做，想要有

 

 

 

注意当所有图层都满足时，两个约束是如何满足的宽度相同。 如果我们也有相同的初始化权重 我们可以得到以下有趣的属性：

 

 

 

我们可以看到，所有图层的权重梯度的方差是相同的，但是当我们考虑更深的网络时，反向传播的梯度的方差可能仍会消失或爆炸。 请注意，这是如何回忆当研究经常性神经网络时发生的问题（Bengio et al。，1994），随着时间的推移，它可以被看作非常深的网络。 我们使用的标准初始化（eq.1）会导致与以下属性的差异：

 

 

 

其中n是图层大小（假设所有图层都相同尺寸）。 这将导致反向传播的变化梯度依赖于图层（并减少）。因此，归一化因子可能因此很重要由于乘法效应初始化深度网络通过图层，我们建议进行以下初始化程序大致满足我们的目标保持激活差异和反向传播梯度随着网络向上或向下移动而变化。 我们将其称为标准化初始化：

 

 

 

其中n是图层大小（假设所有图层都相同尺寸）。 这将导致反向传播的变化梯度依赖于图层（并减少）。因此，归一化因子可能因此很重要由于乘法效应初始化深度网络通过图层，我们建议进行以下初始化程序大致满足我们的目标保持激活差异和反向传播梯度随着网络向上或向下移动而变化。 我们将其称为标准化初始化：

我们监视相关雅可比矩阵的奇异值与第一层：

 

 

 

连续图层具有相同的尺寸时，平均值奇异值对应于无穷小的平均比率从zi到zi + 1映射的卷，以及从zi的平均激活方差的比例到zi + 1。 通过我们的标准化初始化，这个比率是在0.8左右，而标准初始化下降了降至0.5。

 

 

图6：使用归一化直方图的激活值双曲正切激活，标准（顶部）与标准化初始化（底部）。 上图：0峰值增加更高层次。

4.3学习过程中的后向传播梯度

这种网络中的学习动态非常复杂，我们希望开发更好的工具来分析和跟踪它们。 特别是，我们不能在理论分析中使用简单的方差计算，因为权值不再与激活值无关，并且线性假设也被违反。 正如Bradley（2009）首先指出的那样，我们观察到（图7），在训练开始时，在标准初始化（方程1）之后，向后传播的向后传播梯度的方差变小。 然而，我们发现这种趋势在学习期间很快就会逆转。 使用我们的标准化初始化，我们看不到如此递减的反向传播梯度（图7的底部）。

 

 

图7：反向传播梯度归一化直方图用双曲线正切激活，与标准（上）与标准化（下）初始化。 顶部：0-峰值对于更高层而言降低。

最初令人惊讶的是，即使当后向传播梯度变小（标准初始化）时，如图8所示，各层间权重梯度的方差大致保持不变。然而，这可以通过我们上面的理论分析来解释等式14）。有趣的是，如图9所示，这些关于标准和规范化初始化权重梯度的观察结果在训练期间发生了变化（这里为tanh网络）。事实上，尽管梯度起初大致相同，但随着训练的进行，它们彼此不同（在较低层中梯度较大），特别是在标准初始化时。请注意，这可能是归一化初始化的优点之一，因为在不同层次上具有非常不同幅度的梯度可能会导致病态调节和较慢的训练。最后，我们观察到softsign网络与标准化初始化的tanh网络有相似之处，这可以通过比较两种情况下的激活演变来看出（参见图3-底部和图10）。

5误差曲线和结论

我们关心的最后一点是使用不同策略进行培训的成功，并且最好用错误曲线来说明，这些错误曲线显示随着培训进程和渐近线的发展，测试错误的演变。 图11显示了在Shapeset-3×2上进行在线培训的曲线，而表1给出了所有研究数据集（Shapeset-3×2，MNIST，CIFAR-10和Small-ImageNet）的最终测试误差。 作为基准，我们对10万个Shapeset样例优化了RBF支持向量机模型，并获得了59.47％的测试误差，而在同一组中，我们获得了50.47％的具有标准化初始化的深度为5的双曲正切网络。

这些结果说明了选择激活和初始化的效果。 作为一个参考，我们在图11中包括了在无监督预训练和去噪自动编码器之后从初始化获得的监督微调的误差曲线（Vincent等，2008）。 对于每个网络，分别选择学习率来最小化验证集上的错误。 我们可以指出，在Shapeset-3×2上，由于任务的困难，我们在学习过程中观察到重要的饱和度，这可能解释了归一化初始化或软标记效果更明显。

 

 

图8：使用双曲线的权重梯度归一化直方图正切初始化后的切线激活标准初始化（顶部）和标准化初始化（底部），用于不同的层。 即使与标准初始化向后传播的渐变变得更小，重量梯度不！

表1：具有不同激活功能和测试错误的测试错误，具有5个隐藏层的深度网络的初始化方案。N在激活功能名称之后指示使用的标准化初始化。 粗体结果是统计学上的与零假设检验下的非粗体不同与p = 0.005。

 

训练后的自动编码器进行无监督预训练（Vincent et al。，2008），从初始化获得监督微调的误差曲线。对于每个网络，分别选择学习率来最小化验证集上的错误。我们可以指出，在Shapeset-3×2上，由于任务的困难，我们在学习过程中观察到重要的饱和度，这可能解释了归一化初始化或软标记效果更明显。从这些误差曲线中可以得出几点结论：•更经典的具有S形或双曲线正切单位的经典神经网络和标准初始化费用相当差，收敛速度更慢，并且显然趋向于最终较差的局部最小值。 •softsign网络似乎比初始化过程更稳健，可能是因为它们的温和非线性。 •对于tanh网络，建议的标准化初始化可能非常有用，大概是因为层到层转换保持了大小的

其他方法可以缓解学习期间图层之间的差异，例如利用二阶信息为每个参数单独设置学习速率。例如，我们可以利用Hessian的对角线（LeCun et al。，1998b）或梯度方差估计。这两种方法都已经应用于具有双曲正切和标准初始化的Shapeset-3×2。我们观察到性能有所增加，但没有达到标准化初始化的结果。另外，通过将归一化初始化与二阶方法相结合，我们观察到进一步的收益：估计的Hessian可能会关注单元之间的差异，而不必纠正层之间的重要初始差异。在所有报道的实验中，我们使用了每层相同数量的单位。但是，我们验证了当层大小随层编号增加（或减小）时，我们获得相同的增益。本研究的其他结论如下：训练迭代是理解深网训练困难的有力调查工具。 •当从小随机权重初始化时，应避免Sigmoid激活（不对称于0左右），因为它们产生较差的学习动态，并且最初的隐藏层饱和。 •保持层到层的转换，使得激活和梯度都能很好地流动（即雅可比矩在1左右）似乎很有帮助，并且允许纯监督的深层网络与预监督的无监督学习之间的差异的很大一部分。 •我们的许多观察结果仍未得到解释，表明进一步调查以更好地理解深层架构中的梯度和训练动态。

 

 

图11：在线培训期间的测试错误Shapeset-3×2数据集，用于各种激活功能和初始化方案（从上到下按顺序排列最终错误）。 N激活函数名称后表示使用规范化的初始化。

 

 

图12：在MNIST和MST上训练期间的测试错误曲线CIFAR10，用于各种激活功能和初始化计划（在最后阶段从上到下排列）错误）。 N在激活函数名称后指示使用规范化的初始化。

 

参考文献

Bengio, Y. (2009). Learning deep architectures for AI. Foundations and Trends in Machine Learning, 2, 1–127. Also published

as a book. Now Publishers, 2009.

Bengio, Y., Lamblin, P., Popovici, D., & Larochelle, H. (2007).

Greedy layer-wise training of deep networks. NIPS 19 (pp.

153–160). MIT Press.

Bengio, Y., Simard, P., & Frasconi, P. (1994). Learning long-term

dependencies with gradient descent is difficult. IEEE Transactions

on Neural Networks, 5, 157–166.

Bergstra, J., Desjardins, G., Lamblin, P., & Bengio, Y. (2009).

Quadratic polynomials learn better image features (Technical

Report 1337). D´epartement d’Informatique et de Recherche

Op´erationnelle, Universit´e de Montr´eal.

Bradley, D. (2009). Learning in modular systems. Doctoral dissertation,

The Robotics Institute, Carnegie Mellon University.

Collobert, R., &Weston, J. (2008). A unified architecture for natural

language processing: Deep neural networks with multitask

learning. ICML 2008.

Erhan, D., Manzagol, P.-A., Bengio, Y., Bengio, S., & Vincent,

P. (2009). The difficulty of training deep architectures and the

effect of unsupervised pre-training. AISTATS’2009 (pp. 153–

160).

Hinton, G. E., Osindero, S., & Teh, Y. (2006). A fast learning

algorithm for deep belief nets. Neural Computation, 18, 1527–

1554.

Krizhevsky, A., & Hinton, G. (2009). Learning multiple layers

of features from tiny images (Technical Report). University of

Toronto.

Larochelle, H., Bengio, Y., Louradour, J., & Lamblin, P. (2009).

Exploring strategies for training deep neural networks. The

Journal of Machine Learning Research, 10, 1–40.

Larochelle, H., Erhan, D., Courville, A., Bergstra, J., & Bengio,

Y. (2007). An empirical evaluation of deep architectures on

problems with many factors of variation. ICML 2007.

LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998a).

Gradient-based learning applied to document recognition. Proceedings

of the IEEE, 86, 2278–2324.

LeCun, Y., Bottou, L., Orr, G. B., & M¨uller, K.-R. (1998b). Efficient

backprop. In Neural networks, tricks of the trade, Lecture

Notes in Computer Science LNCS 1524. Springer Verlag.

Mnih, A., & Hinton, G. E. (2009). A scalable hierarchical distributed

language model. NIPS 21 (pp. 1081–1088).

Ranzato, M., Poultney, C., Chopra, S., & LeCun, Y. (2007). Efficient

learning of sparse representations with an energy-based

model. NIPS 19.

Rumelhart, D. E., Hinton, G. E., &Williams, R. J. (1986). Learning

representations by back-propagating errors. Nature, 323,

533–536.

Solla, S. A., Levin, E., & Fleisher, M. (1988). Accelerated learning

in layered neural networks. Complex Systems, 2, 625–639.

Vincent, P., Larochelle, H., Bengio, Y., & Manzagol, P.-A. (2008).

Extracting and composing robust features with denoising autoencoders.

ICML 2008.