软件工程基础个人项目——数独终局生成&求解
目录
1.源代码的GitHub链接:
2.PSP表格(预估):
3.题目要求:
4.解题思路:
1)数独游戏规则
2)生成数独终局
2)求解数独
5.设计实现过程:
第一部分:sudoku类的构建
第二部分:check类的构建
第三部分:sudoku生成函数
第四部分:sudoku求解函数
第五部分:check 命令行input部分
第六部分:main函数
单元测试设计部分:
代码覆盖率测试:
6.改进程序性能:
第一次改进后
第二次改进后
第三次改进后:
在powershell上的运行结果:
7.代码说明:
数独终局生成部分:
解数独部分:
8.总结:
期间遇到的问题:
个人总结:
9.GUI界面
1.源代码的GitHub链接:
https://github.com/wenzihan/SudokuProject
2.PSP表格(预估):
| personal software process stage |
预估耗时(分钟) | 实际耗时(分钟) | |
| planning | 计划 | 50 | 40 |
| Estimate | 估计这任务需要多长时间 | 10 | 10 |
| development | 开发 | - | - |
| analysis | 需求分析(包括学习新技术) | 300 | 180 |
| design spec | 生成设计文档 | 60 | 60 |
| design review | 设计复审(和同事审核设计文档) | 30 | 10 |
| coding standard | 代码规范(为目前的开发制定合适的规范) | 10 | 10 |
| design | 具体设计 | 120 | 150 |
| coding | 具体编码 | 1500 | 1800 |
| code review | 代码复审 | 300 | 300 |
| test | 测试(自我测试,修改代码,提交修改) | 120 | 300 |
| reporting | 报告 | 180 | 300 |
| test report | 测试报告 | 30 | 30 |
| size measurement | 计算工作量 | 10 | 10 |
| postmortem&process improvement plan | 事后总结,并提出过程改进计划 | 30 | 20 |
| 合计 | 2750 | 3220 |
3.题目要求:
4.解题思路:
其实我没有玩过数独,,我经常听到别人说自己在初中的时候闲的时候就会做一点数独,可是对于我这个新手,嗯在做题开始之前我还是先了解一下数独的规则吧。
1)数独游戏规则
数独起源于18世纪初瑞士数学家欧拉等人研究的拉丁方阵(Latin Square)。拉丁方块的规则:每一行(Row)、每一列(Column)均含1-N(N即盘面的规格),不重复。这与前面提到的标准数独非常相似,但少了一个宫的规则。
数独 (日语:数独/すうどく sudoku)是一种逻辑性的数字填充游戏。数独盘面是个九宫,每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件,利用逻辑和推理,在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次。每一个粗线宫内的数字均含1-9,不重复。
本次作业的数独问题主要分为生成数独终局和求解数独两大部分。
首先是第一部分:生成数独终局
然后是第二部分:求解数独
2)生成数独终局
本次作业的要求是要能够生成1e6个数独终局,而且每个数独左上角的数字是(学号后两位相加)%9+1,我的左上角数字应该为7。大致阅读了题目要求和规则之后,我参考了几种生成数独终局的算法:有矩阵转换法和随机法。
矩阵转换法:
1.首先要指定一个矩阵作为种子矩阵。为了完成矩阵的转换,我们需要有可用的数独数组作为种子数组才行。
做法可以如下:
1). 先给定几个可用数独数组作为备选种子矩阵。
2). 产生一个随机数,随机选中其中的一个作为种子矩阵。
2.确定矩阵的变换方式。例如交换两个数的位置,或者调整行或列的位置(但是要注意行和列的转换,需要保证的是:交换只发生在前三行,中间三行,最后三行,前三列,中间三列以及最后三列之间。而不能越界交换,比如第一行和第四行交换就是不允许的)调整块的位置,矩阵旋转等等。
矩阵转换法生成数独终盘的方式具有方便速度快的特点。它的缺点产生的终盘的随机性不是很强。
随机法:
1. 写一个方法用于获取一个由1到9九个数随机排列的一维数组。
2. 循环行(下标从0到8),将这个随机产生的一维数组作为当前行的内容,如果是第一行(行标为0),那么直接作为该行的内容。如果是其它行,则验证数据是否都符合条件。
3.如果符合条件,则再产生一个由1到9九个数随机排列的一维数组作为下一行的内容并验证数据是否可用。
4. 如果不符合条件,则将该行数据设置为0,调整row和col,产生一个由1到9九个数随机排列的一维数组,重新对该行验证。
5. 程序中为了防止产生一维随机数组的方法调用很多次而没有产生结果,设置一个最多调用该方法次数的阈值,当达到这个阈值还没有产生结果,重新从 row =0 , col =0 开始。
参考:
- 终盘生成之随机法
- 终盘生成之矩阵转换法
最终结合两种思想研究了数独生成规律,结合其他CSDN实现代码,找到了一个易于实现的生成数独终局的算法,首先随机生成数独的第一行,从第二行开始,每一行是第一行右移3,6,1,4,7,2,5,8列的结果,这样就生成了一个数独终局。我的左上角的第一个数字应该为7,第一行如果是 7 1 2 3 4 5 6 8 9 的话,相应生成矩阵为:
7 1 2 3 4 5 6 8 9
6 8 9 7 1 2 3 4 5
3 4 5 6 8 9 7 1 2
9 7 1 2 3 4 5 6 8
5 6 8 9 7 1 2 3 4
2 3 4 5 6 8 9 7 1
8 9 7 1 2 3 4 5 6
4 5 6 8 9 7 1 2 3
1 2 3 4 5 6 8 9 7
用这种方法共能生成9!=362880种,但是由于左上角已经固定(我的是7),所以只有8!=40320种,不能够满足题目的要求,结合矩阵转换法的思想,我们可以对生成终局的1~3行,4~6行,7~9行任意交换顺序,由于第一行不能动,那我们就只交换4~6行,7~9行,那么每一种第一行确定的数独终局,又能衍生出3!*3!=36种终局,40320*36=1451520>1e6,远远超出题目所要求的数目!
2)求解数独
求解数独我首先想到的是用回溯法,毕竟这个在学习计算机算法的时候也是用的比较熟练比较熟悉的一种,但其实也挺担心回溯法的效率问题于是我又阅读了几篇关于数独求解的博客,get到了一个比较优秀的算法DLX,剩下要做的就是算法学习了。
回溯法思想:
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。 若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。 而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
对于回溯法,我的想法是,对于一个给定的数独题目,算法在解数独题时,在依次决定每个格子的数字时会根据之前已经填入的数字判断当前格子可能填入的数字,然后选择其中一个再去跳到下一个格子。当后面出现无解的情况(一个格子没有可填入的数字),就依次回退到上一个格子,选取下一个可能填入的数字,再依次执行下去。直到填入了最后一个格子,算是完成了数独的一个解。
另外我看在参考别人的代码的时候看到了有用DLX(Dancing links)算法实现求解数独的算法,这个应该是目前最好的求解数独的方法了,具体可以参考 :
- 用DLX解sudoku
- 数独sudoku DLX算法
- Dancing LInks I
DLX算法还有相关博客上的代码基本也看了个大概,最后决定还是先用比较熟悉一点的回溯法,不好的一点就是可能效率不如DLX高一些。当然以后也可以再用DLX自己编着试试。
5.设计实现过程:
最开始我认为这个代码不会太长,感觉全部封装在main.cpp里面就可以了,sudoku生成函数写完的时候,我大致看了一下,觉得可能在我所有代码写完之后看起来会很乱,但还是现在main里面完成了所有的函数,全部函数完成之后才进行进一步封装,其实封装的时候还费了不少时间,由于对面向对象创建类那点知识稍微有点不熟悉了,老是出现未定义之类的错误。这次实验也算是让我重新复习了一下面向对象的基本操作了。封装主要有两大部分,一个是sudoku类的封装,一部分是题目要求所要实现功能函数的封装。设计过程中出现的问题是我始料未及的,封装好之后,在命令行输入"sudoku.exe -c 200"运行过程倒是没有问题,但是出现了找不到写入的sudoku.txt文件的问题,也就是最后在exe同目录下并没有找到相应的txt文件,这是在没有封装之前所不曾发生的。我就在思考这个最终结果写入的txt文件到底应该怎样才能让所封装的这几个函数共享,首先我是想到放在创造的sudoku类的私有变量里面,在执行构造函数时将其打开,但似乎三个cpp文件还是不能够共享resultfile,我尝试了很多种方法换resultfile的地方,由于最开始没封装函数的时候我把这个放在全局,根本就不会出现这种错误。后来把它放在sudoku类的私有变量中,这样所有的共有函数就可以使用了,还是面向对象知识掌握不扎实,这一点我弄了特别久,最终在构造函数中将resultfile打开。后来在改进性能的时候,又把打开sudoku.txt的地方改了,改进后,我分别在两个实现函数中打开,一个作为resultfile1打开,一个作为resultfile2打开。
大致规划了一下,细化的代码主封装在六部分中:
第一部分:sudoku类的构建
类的创建我把它放在一个名为“sudoku.h”的头文件中。类的名字命名为“Sudoku”。类里面是关于这个数独所要实现的函数声明以及数独需要的私有变量。
公有函数:
- void solveSudoku(string path); 这是sudoku求解函数入口
- void createSudoku(int sudokuCount); 这是sudoku生成函数入口
- void backtrace(int count); 这是回溯部分的函数
- bool isPlace(int count); 这是判断赋的值的判断
私有变量:
- char grid[9][9]; 这是在求解数独时读入一个数独题目的存储数组
ofstream resultfile; 这是生成数独或者求解数独最终答案放置的文件- FILE *resultfile1;生成终局时打开的文件
- FILE *resultfile2;解数独时打开的文件
第二部分:check类的构建
check类我把它放在一个名为check.h的头文件中,类的名字为“check”类里面是对从命令行传入的argc和argv参数的分析
公有函数:
- check(int argc, char *argv[]); 分析
- void input_type_analyse(); 传入类型分析
- char get_type();得到命令类型
- int get_num();得到要生成的终局个数
- char* get_filename();得到要读的文件地址
- bool found_error();返回是否有错误
私有变量:
- int argc;
- char **argv;
- int num;个数
- char type; 类型
- char* filename;文件地址
- bool input_error;是否错误
第三部分:sudoku生成函数
这一部分我把它封装在“create.cpp”中,里面有函数createSudoku()。
第四部分:sudoku求解函数
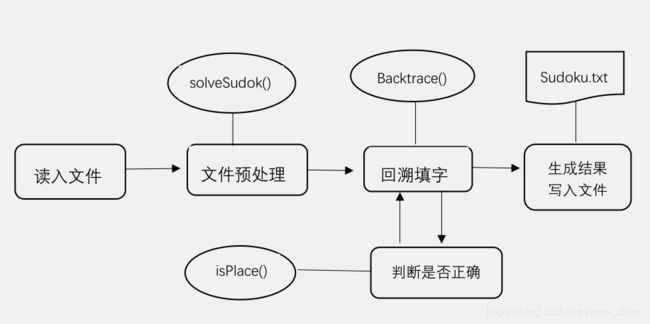
这一部分我把它封装在“solve.cpp”中,里面有solveSudoku函数,它的工作是对读入文件内容进行预处理,将其放在一个grid数组中然后调用回溯函数backtrace。backtrace函数中调用了isPlace函数来进行判断所填数字是否满足要求。
第五部分:check 命令行input部分
这一部分针对check类里面的声明,将几个函数定义写了出来,主要就是判断有无错误产生以及错误的类型
第六部分:main函数
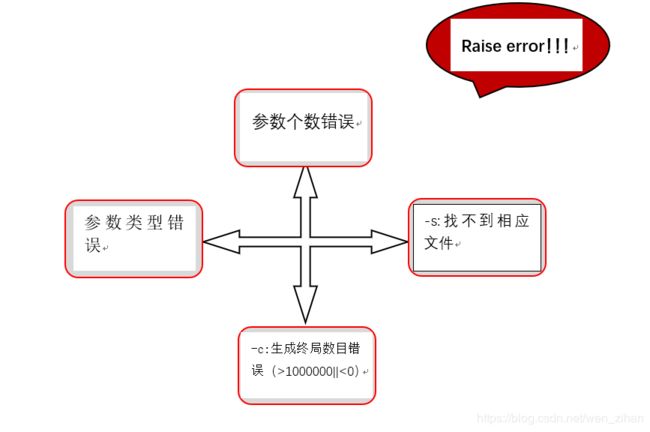
这一部分我把它封装在“main.cpp”中,最开始我的main函数主要是用来判断命令行输入命令要完成的功能类型,并提供解决问题的入口。如果不是要求的两种命令类型需要raise error。后来为了设计单元测试方便,我把对命令行的输入分析又单独封装在一个check类中,所以最后main的功能就是传递命令行参数和调用函数的作用了。
单元测试设计部分:
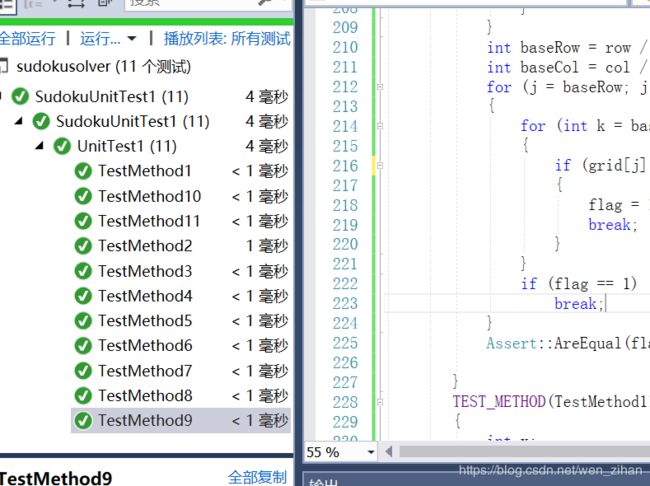
在这个项目中,我一共设计了11个测试,前八个对命令行输入分析的check(),分别测试了它在正确和错误情况下的返回值,第九,十个是对回溯求解的Isplace()的测试,这是解数独的核心操作,第十一个是对生成数独终局的next_permutation(),进行了正确性测试。测试代码已经上传到github上。测试结果如下图所示:
代码覆盖率测试:
代码覆盖率这一部分没有在我的电脑上跑,这一部分需要用到Visual Studio Enterprise版本进行覆盖率测试比较容易,但是我的是Community版本,需要导入open cover才能测试,但是open cover其实测试的还不是整体代码的覆盖率,是一个一个的测试用例所测试出来的覆盖率,所以这一部分最后是拿到了别人的电脑上帮我跑了一下代码覆盖率,结果如下:
6.改进程序性能:
改进程序性能主要是针对生成终局部分的性能进行改进,对于解数独部分,觉得性能的如果要改进的话,就得使用更加6的DLX算法了。
代码最开始提交的时候,在文件写入部分用的是fstream,当时运行终局生成函数createSudoku生成1000000个终局总共花费了有整整三分钟还要多!其实也是主要有一点就是每次的写文件我是一个一个数字写进去的,双层循环外加写文件的时间耗费,想一想就觉得十分可怕,每次跑程序,这个生成的性能是在是令人感到十分的不满意,后来就咨询了一些性能还不错的同学对我的程序I/O部分进行了性能改进。
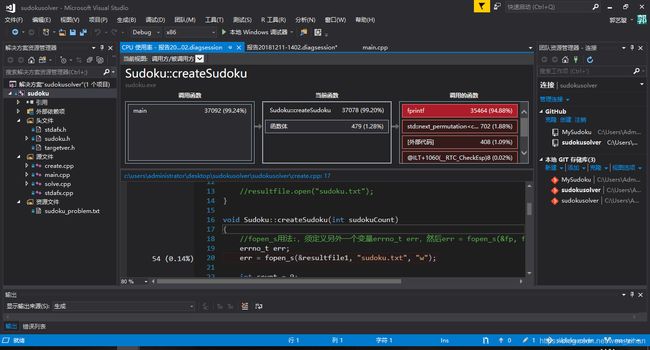
- 第一次改进是把写文件用fprint替换fstream,然后由一个一个矩阵中数字的写入改为一行一行的写进文件resultfile中(其实还是很暴力的方法),这样改进之后我的程序性能提高了好几倍,最后生成终局大概需要四十多秒就可以生成1000000个终局矩阵了。但是这个性能我还是不能满意,通过查看VS自带的性能分析工具,可以看到我的fprint部分,也就是写文件部分占用了90%以上的时间。。。后来又是各种咨询同学,也在网上看了一些关于写文件的性能有关文章,
- 第二次改进是把一个矩阵装入一个数组中,最后将这个数字一次性写进文件。在一部分我构建了一个matrix[162]数组,初始化都为空格,最后隔一个填入一个数字,每18个后面添加一个‘\n’,使用这种方法可以减少很多不停地打开文件关闭文件时间的消耗,最终时间大约为5秒多。
- 第三次改进是仿照每次改进的思想,最终把生成的所有终局结果放在一个非常大的数组中,我把它命名为matx[],最开始申请空间的时候,总是有报错:存储空间栈不足,这类的错误,最后竟然还生成了一个病毒。。。最后找到解决办法是在createSudoku.cpp中写入如下部分:
#pragma region createSudokuStatement
char matx[200000000];
#pragma endregion这样就不会报错啦!
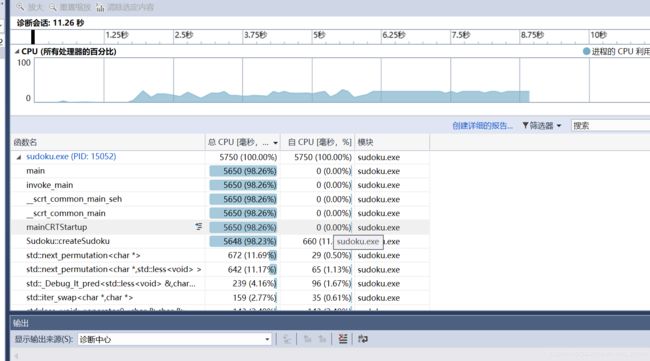
CPU执行代码时的时间耗费情况:
-
第一次改进后
emmm第一次的性能分析并不是在我的电脑上运行的,原因是我在 项目——sudoku属性 中改变命令参数后点击性能分析并没有出现我想要的结果,还是不能正确生成,虽然我也不知道是为什么,,,但是第二次改进之后再次运行性能分析竟然就自己好了,百度也并没有发现这是怎么回事。。。
可以看出在第一次改进之后,时间耗用还是很长的,主要还是在createSudoku()中的fprintf部分占用的大部分的时间。
-
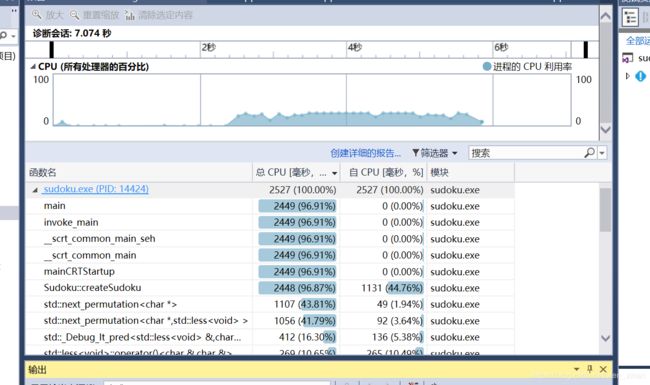
第二次改进后
第二次改进后可以看到fputs部分还是非常耗时的,主要还是因为没能一次全部写入文件。这也为第三次改进提供了思路。
-
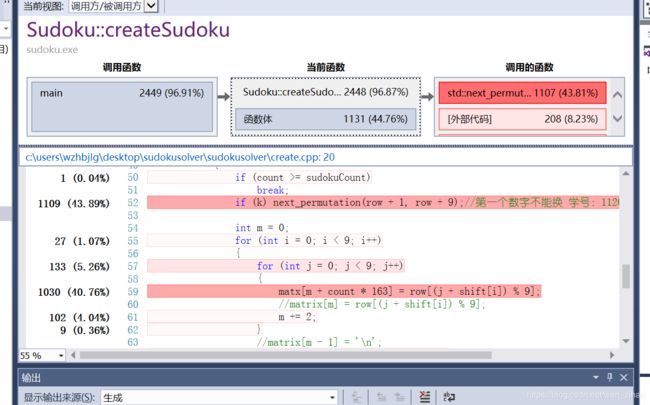
第三次改进后:
可以看到最费时的已经不是fputs函数了,而是一些不可缺少的对字符串和文件的处理部分。第三次改进取得了不错的效果。
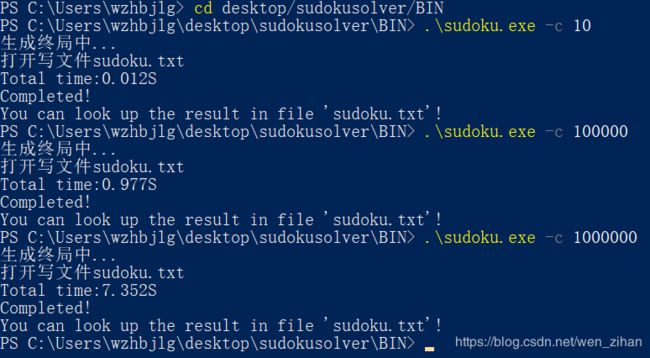
在powershell上的运行结果:
这里计算的时间是由clock函数算出来的,与性能分析里面占用CPU的时间略有出入。
7.代码说明:
数独终局生成部分:
首先打开将要写入的文件sudoku.txt,然后定义一个shift[]数组,表示每一行相对于第一行的移动,用next_permutation()函数来实现对第一行所可能生成顺序的全排列,每一次全排列对应一个shift[]数组所对应的生成矩阵,一个生成矩阵通交换4~6行,7~9行生成更多的终局矩阵,每生成一个,将其存入matx[]矩阵中,存完一个矩阵之后,令matx[i+1]=‘\n’,来保持与下一个矩阵之间的空行。最后将其一次性写入文件中。
void Sudoku::createSudoku(int sudokuCount)
{
//fopen_s用法:,须定义另外一个变量errno_t err,然后err = fopen_s(&fp, filename, "w")。
errno_t err;
err = fopen_s(&resultfile1, "sudoku.txt", "w");
cout << "打开写文件sudoku.txt" << endl;
int count = 0;
//char data_store[200]= {' '};
int shift[9] = { 0, 3, 6, 1, 4, 7, 2, 5, 8 };
for (int i = 0; i < 6; i++)
{
if (count >= sudokuCount)
{
matx[count * 163 - 1] = '\0';
break;
}
if (i)
{
next_permutation(shift + 3, shift + 6); //交换4~6行的任意两行
shift[6] = 2, shift[7] = 5, shift[8] = 8;
}
for (int j = 0; j < 6; j++)
{
if (count >= sudokuCount)
break;
if (j) next_permutation(shift + 6, shift + 9); //交换7~9行的任意两行
char row[10] = "712345689";
for (int k = 0; k < 40320; k++)
{
if (count >= sudokuCount)
break;
if (k) next_permutation(row + 1, row + 9);//第一个数字不能换 学号:1120161760
int m = 0;
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
matx[m + count * 163] = row[(j + shift[i]) % 9];
//matrix[m] = row[(j + shift[i]) % 9];
m += 2;
}
//matrix[m - 1] = '\n';
matx[(m - 1) + 163 * count] = '\n';
}
//matrix[162] = '\n';
matx[162 + 163 * count] = '\n';
// fputs(matrix, resultfile1);
//fputs("\n", resultfile1);
count++;
}
}
}
fputs(matx, resultfile1);
}解数独部分:
从backtrace(0)开始检测这个相应的在矩阵中的数字是不是0,如果是零,对其进行1~9的赋值,每赋值一次,用isplace()函数检测填入数字是否符合规律,主要是对同一行有没有重复,同一列有没有重复,同一宫有没有重复进行检验。如果都没有重复则backtrace(count+1)对矩阵回溯。这里只给出了解数独的核心判断部分。
bool Sudoku::isPlace(int count)
{
int row = count / 9;
int col = count % 9;
int j;
for (j = 0; j < 9; j++) //同一行
{
if (grid[row][j] == grid[row][col] && j != col)
return false;
}
for (j = 0; j < 9; j++) //同一列
{
if (grid[j][col] == grid[row][col] && j != row)
return false;
}
int baseRow = row / 3 * 3;
int baseCol = col / 3 * 3;
for (j = baseRow; j < baseRow + 3; j++) //同一宫
{
for (int k = baseCol; k < baseCol + 3; k++)
{
if (grid[j][k] == grid[row][col] &&(j != row || k != col) )
return false;
}
}
return true;
}8.总结:
期间遇到的问题:
1.明明创建了“Sudoku”类,却提示“Sudoku”不是类或者命名空间名称,这个百度了一下,才知道主要是mfc自定义的类时忘记#include“stdafx.h”,或者是#include“stafx.h”没有放在代码实现的第一行导致,我是第二种错误。
2.在优化函数性能的时候,在网上比较好几种从文件写入读出那种操作比较快,尝试过用“<<"重构,这个速度特别慢,第一次用fputs的时候,将数组写进文件很意外竟然只写进去了数组第一个元素,说实话到现在我都没弄明白是怎么回事,似乎是没有初始化全为空格的原因,致使在后来遇到空格后就不写了。后来在第二次使用的时候将其初始化为空格之后就没有遇到这个问题了。
3.设计单元测试的时候,第一次全部过了,后来第二天打开再跑一次的时候,出现了“A 64-bit test cannot run in a 32-bit process. Specify platform as X64 to force test run in X64 mode on X64 machine.”的错误信息,测试用例全部打叉,,,后来百度了一下,设置测试——测试设置——默认处理器体系结构——x(64) 就好了。看到测试用例全部对勾,心情美美哒。
4.文件的打开地方的问题。要想一个类里面的多个函数使用,在主函数定义是不行的,在其所在cpp文件开头定义也是不能共享的,第一种办法:打开一个文件两个函数公用,在类中私有变量部分定义该文件,在构造函数打开;第二种方法:两个函数使用不同的文件,在私有变量中定义两个不同的文件,在其相应的函数模块打开不同的文件。
5.最后一次性能改进的时候,也想要定义一个大数组,但是数组无法放到createSudoku()函数里面,总会提示栈空间不足的错误。最后使用pragma region 解决了这个问题。pragma region是一个Visio Studio Code Editor中的命令,来定义可以扩展和收缩的代码区域的开头和结尾,可以用来收缩或者展开一段代码。
#pragma region name
.....
#pragma endregion comment个人总结:
在本项目中,很多东西都是以前所没有遇到过的,这就需要我去学习与模仿别人的代码,通过模仿来积累知识和经验。通过这次项目的进行,我学习到了很多关于VS以前所不知道的用法,以前知识单纯的在VS上面写代码,从来没有进行过别的任何工作,而完成一个软件是一个很大的工程,这其中不仅仅是最开始的编程,也包括很多包括需求分析,用例测试,性能分析等等等等。以前并没有用过命令行跑程序,也没有尝试过从命令行传入参数,更没有设计过单元测试,没有进行过性能分析,没有使用过github去commit项目进展,这些我觉得都是在课堂上学不到的,只有真正的去实践才能发现第一次有多不容易。过程很艰辛,走了很多坑,但是我觉得正是这些坑让我学到了更多的东西。相信下一次再做项目会完成的比现在容易很多。
9.GUI界面
这一部分是将上一个项目中生成的终局用挖空函数进行挖空,生成problem.txt,每次把problem.txt中的一个数独矩阵非零部分读入界面。该界面有三个按钮,start是开始,next是做下一个题,submit是提交,如果没有做完,或者错误,正确都会有相应的提示信息。GUI部分功能还可以增强,比如加入限时部分,每道题限时十分钟,以及错误纠正部分。这些后续会慢慢实现。
正确:
错误:
没有完成: