SLAM: SLAM基本流程—VSLAM扫盲之旅

       在很多机器人的论文和书籍里面，劈头第一页即是，经典的SLAM视觉框架是过去十几年前已经成熟的研究结果，这个框架和算法本身已经没有太多理论可以操作的空间。封杀了很多人的SLAM科研之路，把SLAM当一个工程看待。

       在《机器人手册》 第2卷，这本书里面，第23章讲述了：三维视觉和基于视觉的实时定位于地图重建。在第37章里面，讲述了 同时定位与建图。指出了SLAM的三种基本方法。

       

       一种是EKF的方法，但由于性能的约束，逐渐变得非主流；第二种基于图表示，成功使用稀疏非线性优化方法解决SLAM问题，成为主要方法；第三种也是成为粒子滤波器的非参数统计滤波技术，是在线SLAM的一种主流方法。

       线性滤波器方法又称为极大似然方法，图方法使用最小二乘方法，粒子滤波为随机方法。

 

VSLAM扫盲之旅

        作为三维重建-SLAM的入门资料汇总： VSLAM扫盲之旅； ICCV研讨会：实时SLAM的未来以及深度学习与SLAM的比较: http://blog.csdn.NET/qq_18661939/article/details/51919329

      The Future of Real-time SLAM[ZZ]: https://zhuanlan.zhihu.com/p/21738966

      SLAM 开发学习资源与经验分享：https://github.com/GeekLiB/Lee-SLAM-source?utm_source=tuicool&utm_medium=referral

        此文涉及到硬件的讨论，还是值得看一下的，可以大致浏览一下， 速感CEO：  SLAM的前世今生 终于有人说清楚了

 

最近流行的结构光和TOF

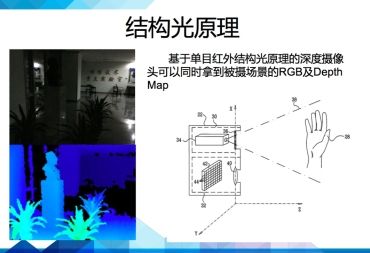
结构光原理的深度摄像机通常具有激光投射器、光学衍射元件（DOE）、红外摄像头三大核心器件。

这个图（右图）摘自primesense的专利。

可以看到primesense的doe是由两部分组成的，一个是扩散片，一个是衍射片。先通过扩散成一个区域的随机散斑，然后复制成九份，投射到了被摄物体上。根据红外摄像头捕捉到的红外散斑，PS1080这个芯片就可以快速解算出各个点的深度信息。

这儿还有两款结构光原理的摄像头。

第一页它是由两幅十分规律的散斑组成，最后同时被红外相机获得，精度相对较高。但据说DOE成本也比较高。

还有一种比较独特的方案（最后一幅图），它采用mems微镜的方式，类似DLP投影仪，将激光器进行调频，通过微镜反射出去，并快速改变微镜姿态，进行行列扫描，实现结构光的投射。（产自ST，ST经常做出一些比较炫的黑科技）。

ToF（time of flight）也是一种很有前景的深度获取方法。

传感器发出经调制的近红外光，遇物体后反射，传感器通过计算光线发射和反射时间差或相位差，来换算被拍摄景物的距离，以产生深度信息。类似于雷达，或者想象一下蝙蝠，softkinetic的DS325采用的就是ToF方案（TI设计的），但是它的接收器微观结构比较特殊，有2个或者更多快门，测ps级别的时间差，但它的单位像素尺寸通常在100um的尺寸，所以目前分辨率不高。以后也会有不错的前景，但我觉得并不是颠覆性的。

 

SLAM系统研究点介绍

         本文主要谈谈SLAM中的各个研究点，为研究生们（应该是博客的多数读者吧）作一个提纲挈领的摘要。然后，我们再就各个小问题，讲讲经典的算法与分类。

         文章链接：http://www.cvrobot.net/research-points-introduction-of-slam-system/

SLAM系统基本流程

         三维重建和SLAM侧重点不一样，三维重建侧重于世界地图的重建，把世界地图准确度和量化标准放在第一位；而SLAM作为simultaneous localization and mapping，侧重于定位，更多应用于机器人生产和应用环境。不管是三维重建和SLAM，都存在使用单目相机和双目相机作为数据源的区别，三维相机可以直接得到图像的深度信息，得到三维点云。

        SLAM的地图重建根据过程和结果的不同，分为稀疏重建和稠密重建，不加后续处理的稠密重建的结果为较为密度均匀稠密的点集，即surface；稀疏重建结果为散布在三维笛卡尔空间中的稀疏点集。单目相机的重建结果一般只能得到稀疏地图。

         应用环境一般先对硬件参数进行测量，经过标定过程，可以测得相机的一些内参，作为工程的初始化参数。相机可以标定的参数为相机内参，在SLAM公式序列中称为“内参矩阵”K、“本质矩阵”E和“基本矩阵”F。

         基于特征点法单目SLAM的基本流程分为几个阶段：

1.视觉里程-基本计算

        1.1 单帧图像特征点提取

              在图像中提取特征点，作为待选点。使用的检测方法一般为fast 角点检测方法，检测显著点，得到特征点位置；根据后续需要，对显著点附近的图像，进行处理，得到一个特征描述子向量（SLAM中一般选用Fast、star、Brief等，少数情况下使用freak、sift ）；

        1.2 相邻帧图像特征点关系匹配

              对相邻帧图像的特征描述子进行匹配，得到内点（匹配点）和外点（未匹配点），内点的匹配关系。 匹配算法一般使用机器学习中的最近邻或者ANN搜索，匹配结果的准确性直接影响到后续相机里程和地图构建过程。

         1.3 计算相机里程R和t

               SLAM的开始，开始使用到相机参数。根据匹配关系，得到相机的旋转和平移变化。

               根据透射模型（针孔相机模型），同一个三维点p在两幅图像中的二维位置p1（x1,y1）p2(x2,y2)关系，结合内参矩阵E或F，得出相机的旋转R和和平移t。

                公式1：p2^t * K^-T * t . R *K^-1 *p1=0

                可形式化为2： E = t R 、 F=K^-T *E*K^-1 、x2^T *E*x1 = p2^T *F *p1=0;

                根据公式1,根据匹配关系和位置，求出E或者F。根据公式2，根据E或F解出R、t。

         1.4 根据相机t计算点深度信息

                 三角测量：在不同位置观察同一个点，根据透射关系和平移距离，计算点到相机的距离-深度（世界坐标系）。

                 三角测量公式：

       在理想状态下，视觉里程可以获取两帧图像间隔的相机六自由度变换（x、y、z平移和 xy、yz、zx旋转（欧拉角计量）），并计算出点在世界坐标系中的三维位置（相对尺度）。

       关键点：特征点检测位置要准确、特征点匹配要精准、相机平移和点的深度要合适（三角测量的角度要合适，不然容易造成计算矩阵病态，造成深度不确定性）。

       解决方法：增加分辨率、使用复杂描述子、使用深度滤波器等。

       

2.视觉里程-连续帧

        累计误差问题： 相邻帧计算，因各种硬件、算法原因造成一定误差，连续帧会造成更大的误差累积。具有噪声的轨迹积分不可避免的有可能严重偏离真实轨迹。

        着重于重建环境的方法论为典型三维重建，重点在于环境地图的匹配，一般重建的模型为稠密表面模型；离线重建并附带恢复机器人/相机轨迹的过程被称为SFM，一般同时处理所有数据；而机器人领域最实用的则是导航，即机器人我在哪儿（地图）、我在地图的哪个方位（六位姿），重点在于计算机器人在世界地图中的当前位姿。

       SFM问题为完全SLAM问题，导航重建问题被称为在线SLAM问题。

一、经典滤波器算法

       在线SLAM问题必定使用在线算法，每一刻处理一个数据项，被称为滤波器算法，是第一个经典的SLAM算法。SLAM问题最先是由Smith Self 和Cheeseman 在1988年提出来的，被认为是实现真正全自主移动机器人的关键。 由 Smith, R.C. and P. Cheeseman, 提出的论文：On the Representation and Estimation of Spatial Uncertainty. 《International Journal of Robotics Research》, 1986. 5(4): p. 56 -- 68.     

      基于统计的滤波器思路，把SLAM写成一个运动方程和观测方程，以最小化这两个方程中的噪声项为目的，使用典型的滤波器思路来解决SLAM问题。

       具体方法：当一个帧到达时，我们能（通过码盘或IMU）测出该帧与上一帧的相对运动，但是存在噪声，是为运动方程。同时，通过传感器对路标的观测，我们测出了机器人与路标间的位姿关系，同样也带有噪声，是为观测方程。通过这两者信息，我们可以预测出机器人在当前时刻的位置。同样，根据以往记录的路标点，我们又能计算出一个卡尔曼增益，以补偿噪声的影响。于是，对当前帧和路标的估计，即是这个预测与更新的不断迭代的过程。

        随后的时间里，Se, S., D. Lowe and J. Little,的论文： Mobile robot localization and mapping with uncertainty using scale-invariant visual landmarks. 《The international Journal of robotics Research》, 2002. 21(8): p. 735--758.中使用了卡尔曼滤波的方法。

        使用EKF的方法是一段时间内的SLAM主流方法。EKF算法使用了贝叶斯准则，是一个作了一阶线性化高斯假设的EM算法。 多线程程序崛起之后，SFM方法引入在线SLAM，作为在线SLAM的补充方法。有些方法摒弃了滤波算法，直接使用VO+SFM方法，仍然能比EKF算法取得更好的结果。

       

二、SFM算法-图模型

         从全局来看SLAM的Agent 位姿和传感器观测序列，和这些状态变量之间的有向关系，可以用一个有向图来描述。因此，SLAM的状态优化问题可以引入图方法优化工具。

        EKF方法是假设了有向图为一阶马尔科夫过程的滤波器方法。方法对运动函数g和状态函数f用泰勒公式展开线性化，取其一阶，为一阶模型。EKF方法使用协方差矩阵描述误差，具有二次型，随着观测点的个数增大呈现平方增长。

        后期一些研究人员把一个可能增加的大地图拆为多个子图覆盖，获得了显著的扩展性。

        随着算力的提升，阶段性完全SLAM获得更大的进展。PTAM方法等大量涌现。

 

References:

        [1].    Smith, R.C. and P. Cheeseman, On the Representation and Estimation of Spatial Uncertainty. International Journal of Robotics Research, 1986. 5(4): p. 56–68.

        [2].    Se, S., D. Lowe and J. Little, Mobile robot localization and mapping with uncertainty using scale-invariant visual landmarks. The international Journal of robotics Research, 2002. 21(8): p. 735–758.

        [3].    Mullane, J., et al., A Random-Finite-Set Approach to Bayesian SLAM. IEEE Transactions on Robotics, 2011.

        [4].    Adams, M., et al., SLAM Gets a PHD: New Concepts in Map Estimation. IEEE Robotics Automation Magazine, 2014. 21(2): p. 26–37.

        [5].    Endres, F., et al., 3-D Mapping With an RGB-D Camera. IEEE Transactions on Robotics, 2014. 30(1): p. 177–187.

        [6].    Forster, C., M. Pizzoli and D. Scaramuzza, SVO: Fast semi-direct monocular visual odometry. 2014, IEEE. p. 15–22.

        [7].    Newcombe, R.A., et al., KinectFusion: Real-time dense surface mapping and tracking. 2011, IEEE. p. 127–136.

     

  声明：

本文编撰和转载自：http://www.cnblogs.com/gaoxiang12/p/4395446.html

如果转载了本文编撰的版本，也请注明转载出处：http://www.cvrobot.net/research-points-introduction-of-slam-system/

如果您对该机器学习、图像视觉算法技术感兴趣，可以关注新浪微博：视觉机器人  或者加入 QQ群：101371386