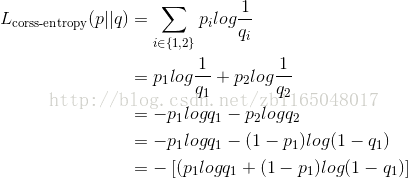KL散度(相对熵)、交叉熵的解析
1 前言
注意两个名词的区别:
相对熵:Kullback–Leibler divergence
交叉熵:cross entropy
KL距离的几个用途:
① 衡量两个概率分布的差异。
② 衡量利用概率分布Q 拟合概率分布P 时的能量损耗,也就是说拟合以后丢失了多少的信息,可以参考前面曲线拟合的思想。
③ 对①的另一种说法,就是衡量两个概率分布的相似度,在运动捕捉里面可以衡量未添加标签的运动与已添加标签的运动,进而进行运动的分类。
百度百科解释的为什么KL距离不准确,不满足距离的概念:
①KL散度不对称,即P到Q的距离,不等于Q到P的距离
②KL散度不满足三角距离公式,两边之和大于第三边,两边之差小于第三边。
2. 相对熵数学定义
![]()
KL散度的值始终大于0,并且当且仅当两分布相同时,KL散度等于0.
从另一个角度也就可以发现,当P(x)和Q(x) 的相似度越高,KL距离越小。
有一个实例,可以参考:http://www.cnblogs.com/finallyliuyu/archive/2010/03/12/1684015.html
3. 交叉熵和相对熵
转自知乎:https://www.zhihu.com/question/41252833
作者:do Cre
链接:https://www.zhihu.com/question/41252833/answer/108777563
来源:知乎
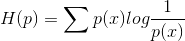
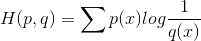

链接:https://www.zhihu.com/question/41252833/answer/108777563
来源:知乎
如果使用错误分布q来表示来自真实分布p的平均编码长度,则应该是:
因为用q来编码的样本来自分布p,所以期望H(p,q)中概率是p(i)。H(p,q)我们称之为“
交叉熵”。
比如含有4个字母(A,B,C,D)的数据集中,真实分布p=(1/2, 1/2, 0, 0),即A和B出现的概率均为1/2,C和D出现的概率都为0。计算H(p)为1,即只需要1位编码即可识别A和B。如果使用分布Q=(1/4, 1/4, 1/4, 1/4)来编码则得到H(p,q)=2,即需要2位编码来识别A和B(当然还有C和D,尽管C和D并不会出现,因为真实分布p中C和D出现的概率为0,这里就钦定概率为0的事件不会发生啦)。
可以看到上例中根据非真实分布q得到的平均编码长度H(p,q)大于根据真实分布p得到的平均编码长度H(p)。事实上,根据 Gibbs' inequality 可知,H(p,q)>=H(p)恒成立,当q为真实分布p时取等号。我们将由q得到的平均编码长度比由p得到的平均编码长度多出的bit数称为“ 相对熵”:
比如含有4个字母(A,B,C,D)的数据集中,真实分布p=(1/2, 1/2, 0, 0),即A和B出现的概率均为1/2,C和D出现的概率都为0。计算H(p)为1,即只需要1位编码即可识别A和B。如果使用分布Q=(1/4, 1/4, 1/4, 1/4)来编码则得到H(p,q)=2,即需要2位编码来识别A和B(当然还有C和D,尽管C和D并不会出现,因为真实分布p中C和D出现的概率为0,这里就钦定概率为0的事件不会发生啦)。
可以看到上例中根据非真实分布q得到的平均编码长度H(p,q)大于根据真实分布p得到的平均编码长度H(p)。事实上,根据 Gibbs' inequality 可知,H(p,q)>=H(p)恒成立,当q为真实分布p时取等号。我们将由q得到的平均编码长度比由p得到的平均编码长度多出的bit数称为“ 相对熵”:
其又被称为KL散度(Kullback–Leibler divergence,KLD) Kullback–Leibler divergence
。它表示2个函数或概率分布的差异性:差异越大则相对熵越大,差异越小则相对熵越小,特别地,若2者相同则熵为0。注意,KL散度的非对称性。
比如TD-IDF算法就可以理解为相对熵的应用:词频在整个语料库的分布与词频在具体文档中分布之间的差异性。
交叉熵可在神经网络(机器学习)中作为损失函数,p表示真实标记的分布,q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题,因为学习速率可以被输出的误差所控制。
PS:通常“相对熵”也可称为“交叉熵”,虽然公式上看 相对熵=交叉熵-信息熵,但由于真实分布p是固定的,D(p||q)由H(p,q)决定。当然也有特殊情况,彼时2者须区别对待。
比如TD-IDF算法就可以理解为相对熵的应用:词频在整个语料库的分布与词频在具体文档中分布之间的差异性。
交叉熵可在神经网络(机器学习)中作为损失函数,p表示真实标记的分布,q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题,因为学习速率可以被输出的误差所控制。
PS:通常“相对熵”也可称为“交叉熵”,虽然公式上看 相对熵=交叉熵-信息熵,但由于真实分布p是固定的,D(p||q)由H(p,q)决定。当然也有特殊情况,彼时2者须区别对待。
稍微说一下中间那个例子,如果真正去计算的话,会发现H(p)=log2,而H(p,q)=log4,然后由于编码位数必须为整数,所以是向上取整,即得到原作者的答案。
4. 交叉熵损失函数
看到交叉熵,想到机器学习中刚好有“交叉熵损失函数”这个东东,好像是针对二分类的情况,可以将前面的交叉熵公式改成二分类的情况:
交叉熵中用q拟合p,其中的q相当于预测值,p相当于正确的标签
如果想好看点,那么一般的写法就是,把y当做正确标签,o当做网络输出,那么
这样就跟我们经常看到的交叉熵损失函数一模一样了。
5.附录
对数回归的损失函数就是这样的,详细请看我后面的博客
softmax理论及代码解读——UFLDL
使用交叉熵损失函数相对于使用均方误差函数的优势请戳