深度学习笔记三：线性神经网络，delta学习规则，梯度下降法

这里我们提出一个神经网络解决异或问题

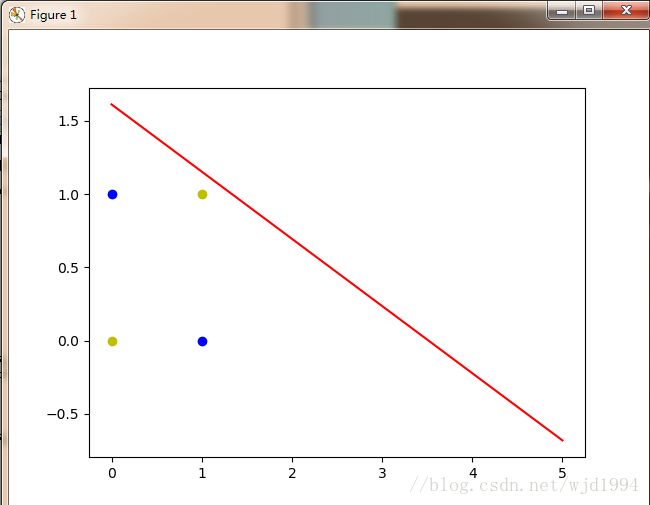
异或问题出现四个点，此时一条直线无法正确地区分出正负样本

X = np.array([[1,0,0],[1,0,1],[1,1,0],[1,1,1]])

Y = np.array([-1,1,1,-1])

x1 = [0,1]
y1 = [1,0]
x2 = [0,1]
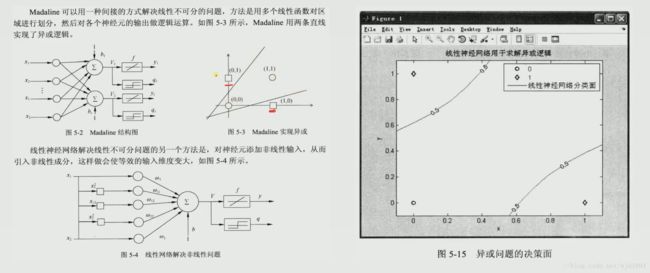
y2 = [0,1]

于是我们引入线性神经网络

线性神经网络解决线性不可分问题

下面给出实现代码：

import numpy as np
import matplotlib.pyplot as plt


X = np.array([[1,0,0,0,0,0],
              [1,0,1,0,0,1],
              [1,1,0,1,0,0],
              [1,1,1,1,1,1]])

Y = np.array([-1,1,1,-1])

W = (np.random.random(6)-0.5)*2

print(W)
#学习率
lr = 0.11

n = 0

o = 0

def update():
    global X,Y,W,lr,n
    n += 1
    o = np.dot(X,W.T)
    W_C = lr*((Y-o.T).dot(X))/X.shape[0]
    W = W + W_C

def predict(X):
    global W
    y = np.sign(np.dot(X,W.T))
    return y

def calculate(x,root):
    a = W[5]
    b = W[2]+x*W[4]
    c = W[0]+x*W[1]+x*x*W[3]
    if root==1:
        return (-b+np.sqrt(b*b-4*a*c))/(2*a)
    if root==2:
        return (-b-np.sqrt(b*b-4*a*c))/(2*a)
    
for i in range(10000):
    update()
    #print(W)
    #print(n)
    #o = np.sign(np.dot(X,W.T))
    if(o == Y.T).all():
        print('finish')
        break
    
for e in X:
    print(predict(e))

x1 = [0,1]
y1 = [1,0]
x2 = [0,1]
y2 = [0,1]
xdata = np.linspace(0,5)

k = -W[1]/W[2]
d = -W[0]/W[2]

plt.figure()
plt.plot(xdata,calculate(xdata,1),'r')
plt.plot(xdata,calculate(xdata,2),'r')
plt.plot(x1,y1,'bo')
plt.plot(x2,y2,'yo')
plt.show()