- 第 20 课时:GPU 管理和 Device Plugin 工作机制(车漾)
阿里云云原生
CNCFX阿里巴巴云原生技术公开课阿里云KubernetesCNCF专家团队CNCF专家团队CNCF专家团队Kubernetes
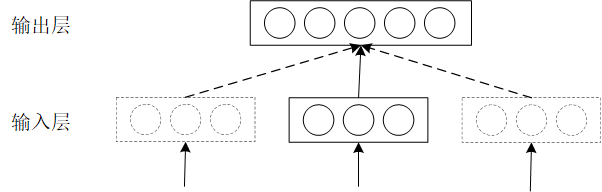
本文将主要分享以下几个方面的内容:需求来源GPU的容器化Kubernetes的GPU管理工作原理课后思考与实践需求来源2016年,随着AlphaGo的走红和TensorFlow项目的异军突起,一场名为AI的技术革命迅速从学术圈蔓延到了工业界,所谓AI革命从此拉开了帷幕。经过三年的发展,AI有了许许多多的落地场景,包括智能客服、人脸识别、机器翻译、以图搜图等功能。其实机器学习或者说是人工智能,并不是
- Docker安装Nginx
坚定的小辣鸡在努力
Dockerdockernginxjava
Docker安装Nginx阅读原文https://www.xiaozaoshu.top/articles/docker-nginxdocker拉取镜像与启动容器在前边的文章中我们已经成功的安装了docker并测试了相关的拉取。dockerpulldocker.1ms.run/nginx:1.27.3-perl接下来我们开始进行Nginx的安装与配置先查看一下我们的镜像[root@xiaozaosh
- 在python程序中调用java代码
Meryoufdd
javajvm开发语言
在python程序中调用java代码Python是一门“胶水”语言,非常灵活多变,但是在一些特殊的时候,也需要调用其它语言来协助实现更多的功能;在公司使用python进行接口测试的时候,会遇到有些接口数据是由公司的开发人员进行自定义的加密算法进行加密的,此时,要开发告诉加密代码是不太可能的。跟开发小哥沟通时,很多时候都是由他给一个jar包,然后剩下的就由测试人员来发挥了。那python该如何使用这
- 学习日志14 python
im_AMBER
学习python开发语言
1divmod(a,b)divmod(a,b)是Python内置函数,用于返回两个数相除的商和余数,返回值是一个元组(tuple)。divmod(a,b)是Python的内置函数,用于同时计算两个数值的商和余数,返回一个包含这两个结果的元组(商,余数)。该函数在处理需要同时获取整除结果和余数的场景(如时间单位转换、分页计算)时非常高效。基本用法python运行result=divmod(a,b)#
- 离线部署视觉模型Qwen2.5-VL方案【企业应用级】
LensonYuan
机器视觉自然语言处理qwenvl视觉模型大模型部署qwen2.5qwen2.5环境qwen2.5-vl镜像包
离线多卡部署视觉模型Qwen2.5-VL企业级服务方案一、背景公司网络是有严格限制,所有涉及境外服务器的网站都无法访问,包括docker等镜像源。本教程,是在提前下载或构建好资源,通过上传到服务器后,做离线部署。二、参考环境大模型服务发布工具:VLLM=0.7.2。大模型版本:qwen2.5-vl-7b,其他版本也可。python版本:python==3.12。环境可选:docker或直接pyth
- Web开发 02
im_AMBER
前端学习
今天梳理出的HTML+CSS核心知识点,涵盖基础结构、布局、样式优化等实用技巧:总结1一、HTML核心知识1.基础结构文档声明:定义文档为HTML5标准。基本标签::根元素,包裹整个页面。:元数据(标题、样式、脚本等),不显示在页面。:设置网页标题(浏览器标签显示)。:页面内容容器,所有可见内容写在这里。2.常用标签文本与标题:~:标题标签,自动加粗且有默认层级样式。:段落标签,默认有上下边距。图
- Java BPM量子引擎:用代码折叠时空,让企业流程快到违反物理定律!
墨夶
Java学习资料4java开发语言
企业流程的"薛定谔困境"与破局之道老张的茶话会:“企业流程像薛定谔的猫——你永远不知道下一秒是卡在审批还是烂在沟通!但Java能用代码让它’量子坍缩’到最优路径!”数据说话:传统流程平均耗时:72小时→优化后仅需18分钟流程执行成功率:优化前68%→优化后99.9%并发处理能力:单实例支持1000+流程实例核心矛盾:“企业流程像’薛定谔的审批’——测不准路径,调不好节点?Java用代码让它’量子化
- 曼城“非常热衷于”签下皇家马德里目标,财务计划已到位,来挑战西甲巨人的明星前锋
无影小优
几个月来,英超冠军一直与这位21岁的射手的转会联系在一起,因为他们试图获得一名顶级中锋的服务,以取代塞尔吉奥·阿奎罗,后者于6月签约巴塞罗那。在未能确保托特纳姆热刺护身符哈里·凯恩在夏天的到来之后,瓜迪奥拉的球队正在寻求捍卫他们的联赛冠军,并可能在冠军联赛中更进一步,而他们的队伍中没有一名不折不扣的前锋。最近有报道称,曼城计划在未来几周和几个月与哈兰德的代表举行会议,讨论夏季转会阿提哈德球场的可能
- 2018-10-10
wangkj
姓名:王康军公司:常州新日催化剂有限公司【日精进打卡第146天】【知-学习】【经典名句】知行合一,知道了不等于做到了!中间还隔着实践【行-实践】1.测试中心热电偶百度沸水校正2.与同事真心交流3.确认测试试剂到货时间4.快乐会议,快乐活动积善:发愿从2018年4月15日起三年内行善1000件,今日1善,共计167善省~悟部门管理中的破棉烂絮,正是自己个人问题的真实写照,为了同事幸福唯有自己努力提高
- 出自《道德经》的52个成语
樂伊李_李昂梁
1、玄之又玄【解释】:形容非常奥妙,不易理解。【出自】:第一章:“玄之又玄,众妙之门。”2、有无相生【解释】:有和无是可以相互转化的。也指矛盾双方的对立与转化,阴阳相生的关系。【出自】:第二章:“有无相生,难易相成,长短相形,高下相盈,音声相和,前后相随,恒也。”3、功成不居【解释】:任其自然存在,不去占为己有。后形容立了功而不把功劳归于自己。【出自】:第二章:“为而弗恃,功成而弗居也。”4、和光
- 谢谢你,小罗!
南希_c83c
这次回乡下过年,个人表现还算满意。在乡下的日子里做到了很勤劳。听到不中听的话,虽然心里不舒服,但却没有怼回去。这也算是一种进步吧。对孩子没有做完的作业,眼看着开学一天天的到来,心里替他们焦急得要命。说到学习,最想感谢的应该是年前给女儿补习的李老师吧!一个年轻又帅气的小伙子。在我最无奈迷茫的时候,接住了我的焦虑。给了我很大的勇气和信心。也给女儿带来了很多的理解与支持。对她也很关爱,是个非常有耐心的一
- 小白学Python,压缩和解压文件
目录前言一、判断文件是否为Zip文件二、打开压缩文件三、解压文件四、获取Zip文件中文件的属性信息前言Python标准库中的zipfile库可用于处理压缩文件,.zip是一种常用的压缩文件格式。zipfile库中包含用于查看Zip文件、解压Zip文件、将文件压缩为Zip文件等的方法。需要注意的是,在使用zipfile库前需要使用import导入zipfile库。一、判断文件是否为Zip文件zipf
- 智慧后厨检测算法构建智能厨房防护网
智驱力人工智能
人工智能算法高温预警行为识别口罩识别食品安全手套识别
智慧后厨检测:构建安全洁净厨房的智能解决方案背景:传统后厨管理的痛点与智慧化需求餐饮行业后厨管理长期面临操作规范难落实、安全隐患难察觉、卫生状况难追溯等痛点。传统人工巡检效率低、覆盖面有限,难以实现24小时无死角监管。例如,厨师未佩戴口罩或手套、违规使用手机、动火离人等行为,可能引发食品安全事故或火灾风险。随着人工智能技术的成熟,智慧后厨检测系统通过集成多种算法,实现了对后厨人员行为、环境卫生、设
- Python 魔术方法
坚定的小辣鸡在努力
Pythonpython开发语言
Python魔术方法Python中的魔术方法(MagicMethods),又叫“双下方法(dundermethods)”,像__init__、__str__、__eq__这样的名字,是Python面向对象非常强大的特性。阅读原文https://www.xiaozaoshu.top/articles/python/maigc-method常用魔术方法详解最常见也最有用的几个魔术方法:1.__init
- 回顾一下Docker的基本操作
William一直在路上
职业重启计划工作心得dockereureka容器
基本操作Docker是一个开源的应用容器引擎,使用Docker可以更轻松地创建、部署和运行应用程序。下面介绍Docker的一些基本操作,主要包括镜像操作、容器操作、仓库操作这几个方面:镜像操作搜索镜像:使用dockersearch命令可以搜索DockerHub上的镜像。例如,搜索Nginx镜像:dockersearchnginx该命令会列出与Nginx相关的镜像,包含镜像的名称、描述、星级评价等信
- 配音每天必练基本功,学配音在哪里学比较好
配音就业圈
一、每天必练配音基本功的步骤配音基本功是每位配音演员必须具备的基本技能,为了提高自己的配音水平,兼职副业推荐公众号,配音新手圈,声优配音圈,新配音兼职圈,配音就业圈,鼎音副业,有声新手圈,每天更新各种远程工作与在线兼职,职位包括:写手、程序开发、剪辑、设计、翻译、配音、无门槛、插画、翻译、等等。。。每日更新兼职。每天都要进行必要的练习。步骤如下:1.语音练习:练习发音准确、清晰,锻炼口腔肌肉的灵活
- Docker 与 GPU 训练
wydxry
docker容器运维
以下是Docker与GPU训练相关的核心命令和操作指南,涵盖容器启动、资源监控和调试技巧:1.启用GPU支持的Docker安装NVIDIA容器工具包(必须步骤)#添加源并安装distribution=$(./etc/os-release;echo$ID$VERSION_ID)\&&curl-s-Lhttps://nvidia.github.io/nvidia-docker/gpgkey|sudoa
- 《Python Web 框架深度剖析:Django、Flask 与 FastAPI 的选择之道》
清水白石008
课程教程学习笔记开发语言python前端django
《PythonWeb框架深度剖析:Django、Flask与FastAPI的选择之道》开篇引入:从“胶水语言”到Web架构核心Python,自1991年由GuidovanRossum发布以来,凭借其简洁优雅的语法和强大的生态系统,逐渐成为全球最受欢迎的编程语言之一。它不仅在数据科学、人工智能、自动化脚本等领域大放异彩,更在Web开发领域构建起一套成熟的技术体系。作为一位长期从事Python开发与教
- GIF动画制作工具 GiftedMotion:开源与定制
悦闻闻
本文还有配套的精品资源,点击获取简介:GiftedMotion是一款开源的GIF动画制作工具,它允许用户导入多张图片或视频片段来创建动画,并支持多种编辑选项,如帧速率调整、色彩调整和过渡效果添加。源代码的开放性使得开发者能够深入研究和定制软件,增加了可扩展性和社区支持。该工具在社交媒体、教育和娱乐等多个领域的应用展示了其广泛的实用价值,并为学习编程和图像处理提供了实践平台。1.GIF动画制作工具介
- 从零开始:Android自定义相机应用开发全解析
悦闻闻
本文还有配套的精品资源,点击获取简介:本文深入探讨了在Android平台上开发自定义相机应用的核心技术要点,包括权限申请、创建预览界面、掌握CameraAPI、初始化相机、设置预览回调、拍照和视频录制、处理相机事件、界面交互设计、兼容性测试及性能优化。通过逐步实践这些知识点,开发者可以定制出符合特定需求的相机应用,并确保其在多种Android设备上的表现。1.Android自定义照相机权限与界面创
- 人脸数目统计系统实现:基于OpenCV和C++的人脸识别
本文还有配套的精品资源,点击获取简介:本项目介绍如何利用OpenCV库和C++语言开发一个人脸识别系统,用于统计图像中的人脸数量。内容涵盖人脸识别的基本原理、关键步骤及技术细节,包括使用Haar级联分类器进行人脸检测,并通过C++编程实现从图像处理到人脸统计的全过程。1.人脸识别基本原理与步骤人脸识别技术已经在安全验证、智能家居、社交媒体等多个领域得到了广泛应用。其基本原理是通过分析人脸图像中的特
- 国内能赚钱的10大网络平台
声优配音圈
以下是国内能赚钱的10大平台:兼职副业推荐公众号,配音新手圈,声优配音圈,新配音兼职圈,配音就业圈,鼎音副业,有声新手圈,每天更新各种远程工作与在线兼职,职位包括:写手、程序开发、剪辑、设计、翻译、配音、无门槛、插画、翻译、等等。。。每日更新兼职。淘宝:淘宝是国内最大的电商平台之一,拥有庞大的用户群体和丰富的商品资源,可以通过开店、代销、推广等方式赚取佣金。微信公众号:微信公众号是国内最大的社交媒
- 模型上下文协议(MCP)详解
Edward.W
计算机基础工具pythonpython网络协议jsgo
MCP(ModelContextProtocol)是一种专门为AI模型交互设计的标准化协议,它定义了模型与客户端之间上下文管理的通用规范。以下是MCP的全面介绍:一、MCP协议概述MCP(ModelContextProtocol)是一种轻量级、语言无关的通信协议,旨在解决AI模型交互中的上下文管理问题。它提供了一套标准化的方法来创建、维护和销毁交互上下文,特别适合需要状态保持的AI应用场景。核心设
- 亲子效能Day3
鲤鱼妈咪
打卡日期:2018年12月05日90天打卡累计天数:3/90#和善与坚定并行养育孩子#孩子第一个30天目标:每晚8:30入睡家长第一个30天目标:每天10000步加油宝贝Noah4岁3个月&Leo2岁8个月践行打卡1/301.规律作息:Noah9:00入睡7:00起Leo9:15入睡7:00起床2.亲子阅读:英语阅读绘本打卡3.️今日闪光点:Noah:今天早上小爱提醒起床之后换好衣服去阳台刷牙,用
- 高质量发展正当时 党员干部责无旁贷
wyzzb123
习近平总书记在广东考察时强调,要坚决贯彻党中央战略部署,坚持新发展理念,坚持高质量发展,进一步解放思想、大胆创新、真抓实干、奋发进取。推动广东高质量发展,党员干部队伍建设至关重要,组织建设是党的建设的重要基础,每一名党员干部与高质量发展息息相关,密不可分。“不积跬步,无以至千里”,我国实现高质量发展的道路上,一砖一瓦都来之不易,每一名党员干部都是高质量发展主动力。走高质量发展道路,应坚定理想信念。
- 基于MATLAB的空时编码技术(源码+万字报告+部署讲解等)
炳烛之明科技
matlab人工智能网络通信仿真
目录基于MATLAB的空时编码技术论文IIAbstractIII第1章绪论11.1选题的背景与选题意义11.1.1选题的背景11.1.2选题的意义21.2论文现状21.3主要内容5第2章空时编码技术72.1空时分组码72.2空时网格码102.3分层空时码112.4三种码及空时分组码优点12第三章STBC空时分组码123.1基本原理123.2编码方法153.2.1两发多收天线系统的空时分组编码方法1
- Django母婴商城项目实践(一) - 母婴商城项目介绍
ITB业生
Djangodjango数据库python
1、母婴商城项目介绍1、项目需求分析需求归纳网站提供的搜索功能搜索结果展示:根据销量、价格、上架时间和收藏数量进行排序商品详情展示:商品尺寸、原价、活动价、图片展示、收藏功能与购买功能购买后的订单信息:包含支付金额、购买时间、订单状态等商品购买的在线支付方式:支付宝、微信、银行卡等功能商品库存管理:SKU(StockKeepingUnit,库存量单位)与SPU(StandardProductUni
- 会话技术Cookie和Session详解
@Zeal
JavaWebcookiesession
文章目录会话跟踪技术的概述会话会话跟踪思考CookieCookie的基本使用概念工作流程Cookie的基本使用Cookie的原理Cookie的使用细节存活时间关于cookie中存储特殊字符问题SessionSession的基本使用概念工作流程Session的基本使用Session的原理Session的使用细节浏览器关闭后,session持久化方案Session的钝化与活化(了解)Session销毁
- binwalk
白天的我最菜
错题本开发语言
windows使用这个命令时候发现要shift一直按住,右击打开cmd管理员运行才行pythonsetup.pyinstall否则没有作用自己安装python目录的Scripts文件夹里,参考如下https://www.cnblogs.com/0yst3r-2046/p/12218770.html
- Git 核心操作全解析:从忽略规则到分支实战
越来越无动于衷
elasticsearch大数据搜索引擎
本文结合真实命令行操作记录,深度拆解Git核心功能:忽略文件配置、变更暂存与对比、分支管理、冲突解决及Stash临时工作流,帮你建立从“会用命令”到“理解原理”的完整认知。一、忽略文件:.gitignore配置1.1为什么需要.gitignore?排除日志文件、编译产物、临时文件、编辑器配置等无需版本控制的内容;避免这些文件出现在gitstatus的“未跟踪文件”列表,保持仓库整洁。1.2语法规则
- java杨辉三角
3213213333332132
java基础
package com.algorithm;
/**
* @Description 杨辉三角
* @author FuJianyong
* 2015-1-22上午10:10:59
*/
public class YangHui {
public static void main(String[] args) {
//初始化二维数组长度
int[][] y
- 《大话重构》之大布局的辛酸历史
白糖_
重构
《大话重构》中提到“大布局你伤不起”,如果企图重构一个陈旧的大型系统是有非常大的风险,重构不是想象中那么简单。我目前所在公司正好对产品做了一次“大布局重构”,下面我就分享这个“大布局”项目经验给大家。
背景
公司专注于企业级管理产品软件,企业有大中小之分,在2000年初公司用JSP/Servlet开发了一套针对中
- 电驴链接在线视频播放源码
dubinwei
源码电驴播放器视频ed2k
本项目是个搜索电驴(ed2k)链接的应用,借助于磁力视频播放器(官网:
http://loveandroid.duapp.com/ 开放平台),可以实现在线播放视频,也可以用迅雷或者其他下载工具下载。
项目源码:
http://git.oschina.net/svo/Emule,动态更新。也可从附件中下载。
项目源码依赖于两个库项目,库项目一链接:
http://git.oschina.
- Javascript中函数的toString()方法
周凡杨
JavaScriptjstoStringfunctionobject
简述
The toString() method returns a string representing the source code of the function.
简译之,Javascript的toString()方法返回一个代表函数源代码的字符串。
句法
function.
- struts处理自定义异常
g21121
struts
很多时候我们会用到自定义异常来表示特定的错误情况,自定义异常比较简单,只要分清是运行时异常还是非运行时异常即可,运行时异常不需要捕获,继承自RuntimeException,是由容器自己抛出,例如空指针异常。
非运行时异常继承自Exception,在抛出后需要捕获,例如文件未找到异常。
此处我们用的是非运行时异常,首先定义一个异常LoginException:
/**
* 类描述:登录相
- Linux中find常见用法示例
510888780
linux
Linux中find常见用法示例
·find path -option [ -print ] [ -exec -ok command ] {} \;
find命令的参数;
- SpringMVC的各种参数绑定方式
Harry642
springMVC绑定表单
1. 基本数据类型(以int为例,其他类似):
Controller代码:
@RequestMapping("saysth.do")
public void test(int count) {
}
表单代码:
<form action="saysth.do" method="post&q
- Java 获取Oracle ROWID
aijuans
javaoracle
A ROWID is an identification tag unique for each row of an Oracle Database table. The ROWID can be thought of as a virtual column, containing the ID for each row.
The oracle.sql.ROWID class i
- java获取方法的参数名
antlove
javajdkparametermethodreflect
reflect.ClassInformationUtil.java
package reflect;
import javassist.ClassPool;
import javassist.CtClass;
import javassist.CtMethod;
import javassist.Modifier;
import javassist.bytecode.CodeAtt
- JAVA正则表达式匹配 查找 替换 提取操作
百合不是茶
java正则表达式替换提取查找
正则表达式的查找;主要是用到String类中的split();
String str;
str.split();方法中传入按照什么规则截取,返回一个String数组
常见的截取规则:
str.split("\\.")按照.来截取
str.
- Java中equals()与hashCode()方法详解
bijian1013
javasetequals()hashCode()
一.equals()方法详解
equals()方法在object类中定义如下:
public boolean equals(Object obj) {
return (this == obj);
}
很明显是对两个对象的地址值进行的比较(即比较引用是否相同)。但是我们知道,String 、Math、I
- 精通Oracle10编程SQL(4)使用SQL语句
bijian1013
oracle数据库plsql
--工资级别表
create table SALGRADE
(
GRADE NUMBER(10),
LOSAL NUMBER(10,2),
HISAL NUMBER(10,2)
)
insert into SALGRADE values(1,0,100);
insert into SALGRADE values(2,100,200);
inser
- 【Nginx二】Nginx作为静态文件HTTP服务器
bit1129
HTTP服务器
Nginx作为静态文件HTTP服务器
在本地系统中创建/data/www目录,存放html文件(包括index.html)
创建/data/images目录,存放imags图片
在主配置文件中添加http指令
http {
server {
listen 80;
server_name
- kafka获得最新partition offset
blackproof
kafkapartitionoffset最新
kafka获得partition下标,需要用到kafka的simpleconsumer
import java.util.ArrayList;
import java.util.Collections;
import java.util.Date;
import java.util.HashMap;
import java.util.List;
import java.
- centos 7安装docker两种方式
ronin47
第一种是采用yum 方式
yum install -y docker
- java-60-在O(1)时间删除链表结点
bylijinnan
java
public class DeleteNode_O1_Time {
/**
* Q 60 在O(1)时间删除链表结点
* 给定链表的头指针和一个结点指针(!!),在O(1)时间删除该结点
*
* Assume the list is:
* head->...->nodeToDelete->mNode->nNode->..
- nginx利用proxy_cache来缓存文件
cfyme
cache
user zhangy users;
worker_processes 10;
error_log /var/vlogs/nginx_error.log crit;
pid /var/vlogs/nginx.pid;
#Specifies the value for ma
- [JWFD开源工作流]JWFD嵌入式语法分析器负号的使用问题
comsci
嵌入式
假如我们需要用JWFD的语法分析模块定义一个带负号的方程式,直接在方程式之前添加负号是不正确的,而必须这样做:
string str01 = "a=3.14;b=2.71;c=0;c-((a*a)+(b*b))"
定义一个0整数c,然后用这个整数c去
- 如何集成支付宝官方文档
dai_lm
android
官方文档下载地址
https://b.alipay.com/order/productDetail.htm?productId=2012120700377310&tabId=4#ps-tabinfo-hash
集成的必要条件
1. 需要有自己的Server接收支付宝的消息
2. 需要先制作app,然后提交支付宝审核,通过后才能集成
调试的时候估计会真的扣款,请注意
- 应该在什么时候使用Hadoop
datamachine
hadoop
原帖地址:http://blog.chinaunix.net/uid-301743-id-3925358.html
存档,某些观点与我不谋而合,过度技术化不可取,且hadoop并非万能。
--------------------------------------------万能的分割线--------------------------------
有人问我,“你在大数据和Hado
- 在GridView中对于有外键的字段使用关联模型进行搜索和排序
dcj3sjt126com
yii
在GridView中使用关联模型进行搜索和排序
首先我们有两个模型它们直接有关联:
class Author extends CActiveRecord {
...
}
class Post extends CActiveRecord {
...
function relations() {
return array(
'
- 使用NSString 的格式化大全
dcj3sjt126com
Objective-C
格式定义The format specifiers supported by the NSString formatting methods and CFString formatting functions follow the IEEE printf specification; the specifiers are summarized in Table 1. Note that you c
- 使用activeX插件对象object滚动有重影
蕃薯耀
activeX插件滚动有重影
使用activeX插件对象object滚动有重影 <object style="width:0;" id="abc" classid="CLSID:D3E3970F-2927-9680-BBB4-5D0889909DF6" codebase="activex/OAX339.CAB#
- SpringMVC4零配置
hanqunfeng
springmvc4
基于Servlet3.0规范和SpringMVC4注解式配置方式,实现零xml配置,弄了个小demo,供交流讨论。
项目说明如下:
1.db.sql是项目中用到的表,数据库使用的是oracle11g
2.该项目使用mvn进行管理,私服为自搭建nexus,项目只用到一个第三方 jar,就是oracle的驱动;
3.默认项目为零配置启动,如果需要更改启动方式,请
- 《开源框架那点事儿16》:缓存相关代码的演变
j2eetop
开源框架
问题引入
上次我参与某个大型项目的优化工作,由于系统要求有比较高的TPS,因此就免不了要使用缓冲。
该项目中用的缓冲比较多,有MemCache,有Redis,有的还需要提供二级缓冲,也就是说应用服务器这层也可以设置一些缓冲。
当然去看相关实现代代码的时候,大致是下面的样子。
[java]
view plain
copy
print
?
public vo
- AngularJS浅析
kvhur
JavaScript
概念
AngularJS is a structural framework for dynamic web apps.
了解更多详情请见原文链接:http://www.gbtags.com/gb/share/5726.htm
Directive
扩展html,给html添加声明语句,以便实现自己的需求。对于页面中html元素以ng为前缀的属性名称,ng是angular的命名空间
- 架构师之jdk的bug排查(一)---------------split的点号陷阱
nannan408
split
1.前言.
jdk1.6的lang包的split方法是有bug的,它不能有效识别A.b.c这种类型,导致截取长度始终是0.而对于其他字符,则无此问题.不知道官方有没有修复这个bug.
2.代码
String[] paths = "object.object2.prop11".split("'");
System.ou
- 如何对10亿数据量级的mongoDB作高效的全表扫描
quentinXXZ
mongodb
本文链接:
http://quentinXXZ.iteye.com/blog/2149440
一、正常情况下,不应该有这种需求
首先,大家应该有个概念,标题中的这个问题,在大多情况下是一个伪命题,不应该被提出来。要知道,对于一般较大数据量的数据库,全表查询,这种操作一般情况下是不应该出现的,在做正常查询的时候,如果是范围查询,你至少应该要加上limit。
说一下,
- C语言算法之水仙花数
qiufeihu
c算法
/**
* 水仙花数
*/
#include <stdio.h>
#define N 10
int main()
{
int x,y,z;
for(x=1;x<=N;x++)
for(y=0;y<=N;y++)
for(z=0;z<=N;z++)
if(x*100+y*10+z == x*x*x
- JSP指令
wyzuomumu
jsp
jsp指令的一般语法格式: <%@ 指令名 属性 =”值 ” %>
常用的三种指令: page,include,taglib
page指令语法形式: <%@ page 属性 1=”值 1” 属性 2=”值 2”%>
include指令语法形式: <%@include file=”relative url”%> (jsp可以通过 include