MATLAB--基于PSO算法的0-1背包问题的求解
MATLAB–基于PSO算法的0-1背包问题的求解。
在干活的过程中整理下来的,希望有用。
0-1背包问题是与TSP问题相似的优化算法测试问题,具体描述为:有N件物品和一个容量为v的背包。第i件物品的体积是 ,价值是 。求解将哪些物品放入背包可使物品的体积总和不超过背包的容量,且价值总和最大。
在这里,假设物品数为10,背包的容量为300,每件物品的体积为[95,75,23,73,50,22,6,57,89,98],每件物品的价值为[89,59,19,43,100,72,44,16,7,64]。
- 编码
对于这个实际问题时,首先要解决的问题是编码:对每个物品,我们只有拿取或者不拿两种选择,不能选择装入某物品的一部分,也不能装入同一物品多次,也就是说这是一个离散优化问题,种群中的个体采用二进制编码,用0表示不选择该件物品,1表示选择该件物品。
其次要考虑对这个问题建立数学模型,也就是设计适应度函数。问题要求我们在所放物品总体积不超过背包的容量的前提下,价值总和最大。根据每件物品的体积计算物品总体积,当物品总体积小于等于背包容量时,适应度值很好表示,就是物品的价值总和;而当物品总体积大于背包容量时,我们希望此时的适应度值特别小,这样在选择的过程中,就不易取这个解了,这里取适应度值=物品总价值- afa×(物品总体积-背包容量),我们把afa叫做惩罚函数系数,当然我们也可以简单的将当物品总体积大于背包容量时的适应度值设为0。
下面开始介绍MATLAB程序。
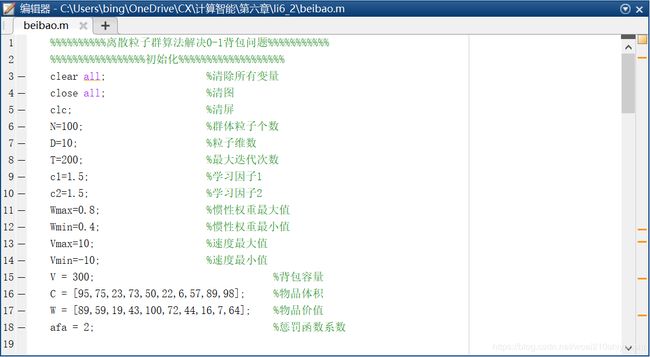
- 1.首先设置算法参数
设置:初始种群粒子个数N=100,粒子维数(即二进制编码长度)D=10,最大选代次数为T=200,学习因子 ,惯性权重最大值为 ,惯性权重最小值为 ,速度最大值为 ,速度最小值为 ,惩罚函数系数 。MATLAB程序如下图,这里先给出截图,代码在文章最后给出。
- 第二步,随机生成初始化种群x,以及随机初始速度v.
对应的MATLAB程序如下。

接着,就根据上边对适应度值的分析,计算初始种群的适应度值,对应的MATLAB程序如下。
这里,f是初始种群x中的一个个体,x(j,:)。另外,如果将当物品总体积大于背包容量时的适应度值设为0,那么对应的MATLAB程序如下。

根据上边程序求得的适应度值,获得粒子个体最优位置p和最优值pbest以及粒子群全局最优位置g和最优值gbest。对应的MATLAB程序如下。
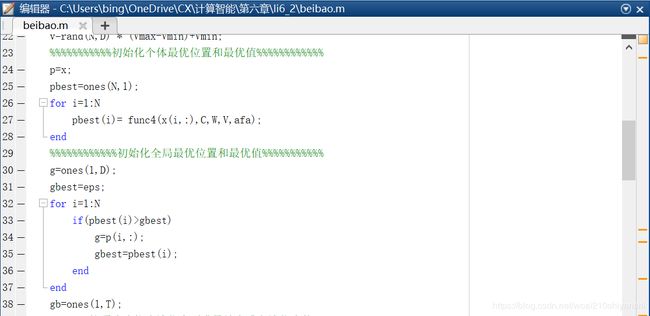
在这段程序里,第31行,gbest=eps;就是先给初始全局最优值gbest设定了一个极小的值。eps是一个函数,它表示的是一个数可以分辨的最小精度。默认时eps=2.2204e-16 。
在第38行,初始化一个(1*T)的矩阵,用来存储历代gbest.
- 第三步,开始进入算法的迭代。
对于每一次迭代中的每一个个体,都要进行以下5步:

其中,计算动态惯性权重值w根据的是书中式(6.14),如下图所示。
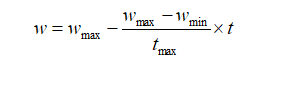
对应的MATLAB程序如下。
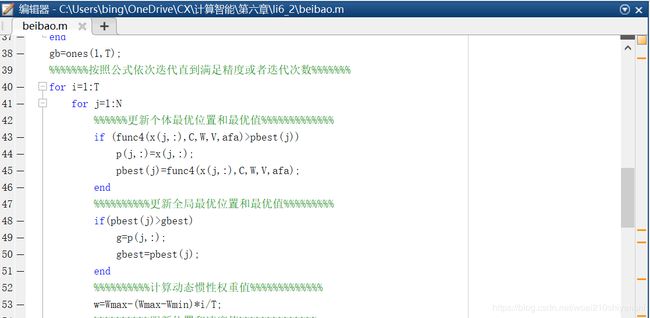
更新位置x及速度v,先根据书中式(6.9)计算速度,对应的MALTLB程序如下。

因为速度v有边界,(在程序第13 14行给出了),所以先对超出边界的速度值进行处理。对应的MALTLB程序如下。
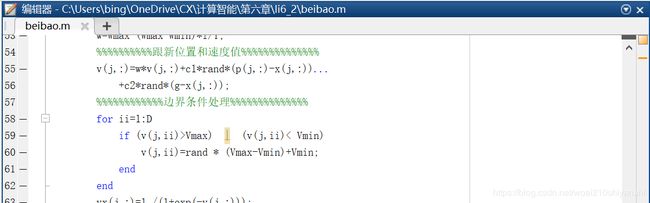
处理完速度v的边界问题后,更新位置x,因为位置x 是二进制编码,也就是x只能是1或者0,对于这类问题,位置更新公式如下所示。
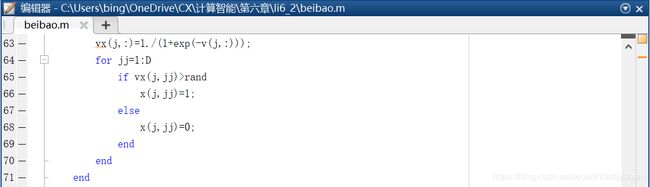
首先,采用sigmoid函数将速度映射v到 [0, 1] 区间,将这个归一化值作为概率,这个概率就是粒子位置下一步取值为1的概率,即。

也就是说,S(Vid)表示粒子位置当前为0的概率,则1- S(Vid) 表示当前为1的概率;如果当前为0,则改变的概率为1- S(Vid) ,如果当前为1,则改变概率为 S(Vid)。对应的MALTLB程序如下。
所有个体经过上述5步操作后,将该次迭代的gbest 存在gb中。对应的MALTLB程序如下。
![]()
T次迭代后,输出寻找到的最优个体g,然后画出历代gbest 随迭代的变化曲线。对应的MALTLB程序如下。

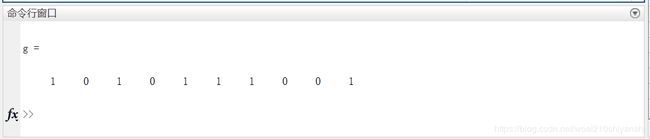
运行程序,最后求得的解如下,0代表没选该物体,1代表选该物体
最后给出整个MATLAB的程序。
%%%%%%%%%%离散粒子群算法解决0-1背包问题%%%%%%%%%%%
%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
N=100; %群体粒子个数
D=10; %粒子维数
T=200; %最大迭代次数
c1=1.5; %学习因子1
c2=1.5; %学习因子2
Wmax=0.8; %惯性权重最大值
Wmin=0.4; %惯性权重最小值
Vmax=10; %速度最大值
Vmin=-10; %速度最小值
V = 300; %背包容量
C = [95,75,23,73,50,22,6,57,89,98]; %物品体积
W = [89,59,19,43,100,72,44,16,7,64]; %物品价值
afa = 2; %惩罚函数系数
%%%%%%%%%初始化种群个体(限定位置和速度)%%%%%%%%%%
x=rand(N,D); %随机获得二进制编码的初始种群
v=rand(N,D) * (Vmax-Vmin)+Vmin;
%%%%%%%%%%%初始化个体最优位置和最优值%%%%%%%%%%%%
p=x;
pbest=ones(N,1);
for i=1:N
pbest(i)= func4(x(i,:),C,W,V,afa);
end
%%%%%%%%%%%%初始化全局最优位置和最优值%%%%%%%%%%%
g=ones(1,D);
gbest=eps;
for i=1:N
if(pbest(i)>gbest)
g=p(i,:);
gbest=pbest(i);
end
end
gb=ones(1,T);
%%%%%%%按照公式依次迭代直到满足精度或者迭代次数%%%%%%%
for i=1:T
for j=1:N
%%%%%%更新个体最优位置和最优值%%%%%%%%%%%%%
if (func4(x(j,:),C,W,V,afa)>pbest(j))
p(j,:)=x(j,:);
pbest(j)=func4(x(j,:),C,W,V,afa);
end
%%%%%%%%%%更新全局最优位置和最优值%%%%%%%%%
if(pbest(j)>gbest)
g=p(j,:);
gbest=pbest(j);
end
%%%%%%%%%%计算动态惯性权重值%%%%%%%%%%%%%
w=Wmax-(Wmax-Wmin)*i/T;
%%%%%%%%%%跟新位置和速度值%%%%%%%%%%%%%%
v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))...
+c2*rand*(g-x(j,:));
%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%
for ii=1:D
if (v(j,ii)>Vmax) | (v(j,ii)< Vmin)
v(j,ii)=rand * (Vmax-Vmin)+Vmin;
end
end
vx(j,:)=1./(1+exp(-v(j,:)));
for jj=1:D
if vx(j,jj)>rand
x(j,jj)=1;
else
x(j,jj)=0;
end
end
end
%%%%%%%%%%%%%记录历代全局最优值%%%%%%%%%%%%
gb(i)=gbest;
end
g %最优个体
figure
plot(gb)
xlabel('迭代次数');
ylabel('适应度值');
title('适应度进化曲线')
%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%%
function result = func4(f,C,W,V,afa)
fit = sum(f.*W);
TotalSize = sum(f.*C);
if TotalSize <= V
fit = fit;
else
fit = fit - afa * (TotalSize - V);
end
result = fit;
end
程序有的部分是根据各种资料整理、然后加上我的改进,出处不详,如果有侵权的请私聊我,我注明出处。