An Introduction to BRDF-Based Lighting——完结
https://www.cs.princeton.edu/courses/archive/fall06/cos526/tmp/wynn.pdf
introduction
the introduction of modern GPUs such as the GeForce 256 and GeForece 2 GTS has opened the door for creating stunning photorealistic interactive 3D content. while the realization of realtime computer-generated images indistinguishable from photographs remains as yet unreached, one piece of machinery that will play an important role in realising interactive photorealism is the notion of a Bi-directional Reflectance Distribution Function (BRDF) and BRDF-based lighting techniques.
the purpose of this tutorial is to provide a working knowledge of the contents and basic mathematics necessary to appreciate BRDFs and to provide some exposure to the terminology used when discussing BRDFs and BRDF-based lighting techniques. if u are already familiar with BRDFs, this paper will be a review; however, if u are new to BRDFs, this paper will provide a good starting point for understanding many reflectance-based lighting techniques.
what is a BRDF?
to understand the concept of a BRDF and how BRDFs can be used to improve realism in interactive computer graphics, we begin by discussing what we know about light and how light interacts with matter.
in general, when light interacts with matter, a complicated light-matter dynamic occurs. this interaction depends on the physical characteristics of the light as well as the physial composition and characteristics of the matter. for example, a rough opaque surface suh as sandpaper will reflect light differently than a smooth reflective surface such as a mirror. figure 1 shows a typical light-matter interation scenario.

From this figure, we make a couple of observations about light. First, when light makes
contact with a material, three types of interactions may occur: light reflection, light
absorption, and light transmittance. That is, some of the incident light is reflected, some
of the light is transmitted, and another portion of the light is absorbed by the medium
itself. Because light is a form of energy, conservation of energy tells us that
![]()
for opaque materials, the majority of incident light is transformed into reflected light and absorbed light. as a result, when an observer views an illuminated surface, what is seen is reflected light, i.e. the light that is reflected towards the observer from all visible surface points. A BRDF describes how much light is reflected when light makes contact with a certain material. Similarly, a BTDF (Bi-directional Transmission Distribution Function) describes how much light is transmitted when light makes contact with a certain material.
in general, the degree to which light is reflected (or transmitted) depends on the viewer and light position relative to the surface normal and tangent. consider, for example, a shiny plasitc teapot illuminated by a white point light source. since the teapot is made of plastic, some surface regions will show a shiny highlight when viewed by an observer. if the observer moves (i.e. changes view direction), the position of the highlight shifts. similarly, if the observer and teapot both remain fixed, but the light source is move, the highlight shifts. since a BRDF measures how light is reflected, it must capture this view- and light- dependent nature of reflected light. consequently, a BRDF is a function of incoming (light) direction and outgoing (view) direction relative to a local orientation at the light interaction point.
Additionally, when light interacts with a surface, different wavelengths (colors) of light may be absorbed, reflected, and transmitted to varying degrees depending upon the physical properties of the material itself. This means that a BRDF is also a function of wavelength.
Finally, light interacts differently with different regions of a surface. This property,
known as positional variance, is most noticeably observed in materials such as wood that
reflect light in a manner that produces surface detail. Both the ringing and striping
patterns often found in wood are indications that the BRDF for wood varies with the
surface spatial position. Many materials exhibit this positional variance because they are
not entirely composed of a single material. Instead, most real world materials are
heterogeneous and have unique material composition properties which vary with the
density and stochastic characteristics of the sub-materials from which they are comprised.
Considering the dependence of a BRDF on the incoming and outgoing directions, the
wavelength of light under consideration, and the positional variance, a general BRDF in
functional notation can be written as

where λ is used to indicate that the BRDF depends on the wavelength under
consideration, the parameters θi, φi, represent the incoming light direction in spherical
coordinates, the parameters θo, φo represent the outgoing reflected direction in spherical
coordinates, and u and v represent the surface position parameterized in texture space. If
you are unfamiliar with spherical coordinates, they are explained in the next section.
Though a BRDF is truly a function of position, sometimes the positional variance is not
included in a BRDF description. Instead, it is common to see a BRDF written as a
function of incoming and outgoing directions and wavelength only (i.e.
( ) λ θ i φi θ o φo BRDF ). Such BRDFs are often called , , , position-invariant or shift-invariant
BRDFs. When the spatial position is not included as a parameter to the function an
assumption is made that the reflectance properties of a material do not vary with spatial
position. In general this is only valid for homogenous materials. One way to introduce
the positional variance is through the use of a detail texture. By adding or modulating the
result of a BRDF lookup with a texture, it is possibly to reasonably approximate a
spatially variant BRDF.
For the remainder of this tutorial, we will denote a position-invariant BRDF in functional
notation as

where λ, θi, φi, θo, and φo have the same meaning as before.
when descrbing a BRDF in this functional notation, it is sometimes convenient to omit the λ subscript for the sake of notation simplicity. When this is done, keep in mind that the values produced by a BRDF do depend on the wavelenth or color channel under consideration. in practice what this means is that in terms of the RGB color convention, the value of the BRDF function must be determined separately for each color channel (i.e. R, G, and B separately). for convenience, it is usually preferred not to specify a particular color channel in the subscript. The implicit assumption is that the programmer
knows that a BRDF value must be determined for each color channel of interest
separately. Given this slightly abbreviated form, the position-invariant BRDF associated
with a single color channel can be considered to be a function of 4 variables. When the
RGB color components are considered as a group, the BRDF is a three-component vector
function.
Spherical Coordinates
Since BRDFs are a function of direction (both light and view), it’s often useful to talk about vectors in terms of spherical coordinates as opposed to cartesian coordinates. This
section presents a very brief review of spherical coordinates that may help you
understand some of the concepts that will be introduced in the next section.
If you are already familiar with spherical coordinates, feel free to skip this section.
Often times when we think of vectors, we think of cartesian-space vectors of the form v=(x y z). While this notation is useful for performing many types of computations, it can be a bit cumbersome when used to parameterize BRDFs. Instead, the spherical
coordinate representation of a vector is generally preferred.
In spherical coordinates, a vector is denoted by a magnitude, ρ, and a pair of angles, θ and φ, which express how far
(angularly) the direction vector differs from two reference basis vectors.
Consider the cartesian and spherical coordinate system shown in figure 2.

Assuming a normalized direction vector, v=(x,y,z), with tail at the origin and head at
an arbitrary position on the +z unit hemisphere, the relationship between the Cartesian
coordinates (vx,vy,vz) and the spherical coordinates (θ, φ) is given by:

Because the vector being considered is assumed to be normalized,

This means that we can represent a direction in spherical coordinates with only two
parameters. By using spherical coordinates to represent directions, a BRDF can be
treated as a wavelength-dependent 4-dimensional function.
Differential Solid Angles
Since BRDFs measure how light reflects off a surface when viewed under various
viewing positions, we must have a good understanding of how much light arrives at a
surface element (or leaves a surface element) from a particular direction. To this end, it
is necessary to introduce the notion of a differential solid angle.
When we talk about light arriving (or leaving) a surface from a certain direction, it’s
more appropriate to speak in terms of the quantity of light arriving at or passing through a
certain area of space. The reason for this is that light is measured in terms of flow
through an area. That is, light is measured as energy per-unit surface area (i.e.
Watts/meter2
). This means it doesn’t really make sense to talk about the amount light
arriving from a single incoming direction – it’s more appropriate to talk about light
coming from a small region of directions. Figure 3 shows an incoming light direction as
well as a small neighborhood of surrounding incoming directions. By taking into account
the amount of light passing through a small cross-sectional area surrounding a direction,
such as that of figure 3, it’s possible to determine the amount of light arriving at a small
surface element.

Figure 3. Since light is measured in terms of energy perunit
area, we must consider flow through a neighborhood
of directions when determining the amount of light
that arrives at or leaves a surface.
the concept of a differential solid angle is a bit theoretical and can be a little tricky to understand at first, but the simplest way to understand its definition is to think of it as the area of a small rectangular region on a unit sphere.

Figure 4. The solid angle is the area of the small patch region on the
surface of the sphere.
Figure 4 shows a unit sphere and a unit vector positioned at the origin. The pyramid
region highlighted on the inside of the sphere represents a volume of directions. The
portion of the unit sphere bounded by the intersection of the pyramid and the unit sphere
form the boundary of a small patch on the sphere’s surface. The differential solid angle
is defined to be the area of this small patch. Given a direction in spherical coordinates
(θ,φ) and small differential angular changes denoted dθ, dφ, the differential solid angle,
dw, is defined to be
Since both the width and the height of the rectangular patch are measured in radians, the
area quantity has units of radians squared (or steradians). Steradians sounds like a fancy
word, but really it’s not too bad. If ever you find the term confusing, just think of it as
“solid angle units” or “radians squared”. The abbreviation for steradians is sr.
In practice, it’s not always necessary to worry about the exact definition of the
differential solid angle. In many situations it’s reasonable to just think of it as the area of
a small surface region uniquely defined for each direction. In the next section and the
remainder of this paper, we will consider a differential solid angle to be the small area on
the unit sphere defined by a neighborhood surrounding a given direction.
The Definition of a BRDF
Up until this point, we haven’t really talked about the exact definition of a BRDF. Now
that we understand the notion of a differential solid angle, we can give a more concrete
definition of a BRDF. Suppose we are given an incoming light direction, wi, and an
outgoing reflected direction, wo, each defined relative to a small surface element. A
BRDF is defined as the ratio of the quantity of reflected light in direction wo, to the
amount of light that reaches the surface from direction wi. To make this clear, let’s call
the quantity of light reflected from the surface in direction wo, Lo, and the amount of light
arriving from direction wi, Ei. Then a BRDF is given by


Now consider figure 5. The figure shows a small surface element (i.e. a pixel/surface point) that is being illuminated by a point light source. The amount of light arriving from direction wi is proportional to the amount of light arriving at the differential solid angle.
Suppose the light source in the figure has intensity Li . Since the differential solid angle
is small, it is essentially a flat region on the hemisphere. As a result, the region is
uniformly illuminated as the same quantity of light, Li, arrives for each position on the
differential solid angle. So the total amount of incoming light arriving through the region
is i i L ∗ dw . The only problem is that this amount of light is with respect to the
differential solid angle and not the actual surface element under consideration. To
determine the amount of light with respect to the surface element, the incoming light
must be “spread out” or projected onto the surface element. This projection is similar to
that which happens with diffuse Lambertian lighting and is accomplished by modulating
that amount by cosθi = N.wi . This means Ei=Licosθidwi . As a result, a BRDF is
given by

From this definition, observe two interesting results. First, a BRDF is not bounded to the
range [0,1] – a common misconception about BRDFs. Although the ratio Lo to Li must
be in [0,1], the division by the cosine term in the denominator implies that a BRDF may
have values larger than 1. Secondly, a BRDF is not a unit-less function. Since the BRDF
definition above includes a division by the solid angle (which has units steradians (sr)),
the units of a BRDF are inverse steradians (sr-1).
Classes and Properties of BRDFs
There are two classes of BRDFs and two important properties. BRDFs can be classified
into two classes: isotropic BRDFs and anisotropic BRDFs. The two important properties
of BRDFs are reciprocity and conservation of energy.
The term isotropic is used to describe BRDFs that represent reflectance properties that
are invariant with respect to rotation of the surface around the surface normal vector.
Consider a small relatively smooth surface element and fix the light and viewer positions.
If we were to rotate the surface about its normal, the BRDF value (and consequently the
resulting illumination) would remain unchanged. Materials with this characteristic such
as smooth plastics have isotropic BRDFs.
Anisotropy, on the other hand, refers to BRDFs that describe reflectance properties that
do exhibit change with respect to rotation of the surface around the surface normal
vector. Some examples of materials that have anisotropic BRDFs are brushed metal,
satin, and hair. In general, most real-world BRDFs are anisotropic to some degree, but
the notion of isotropic BRDFs is useful because many classes of analytical BRDF models
fall within this class. In general, most real-world BRDFs are probably more isotropic
than anisotropic though many real-world surfaces have subtle anisotropy. Any material
that exhibits even the slightest anisotropic reflection has a BRDF that is anisotropic.
BRDFs based on physical laws and considered to be physically plausible have two
properties: reciprocity and conservation of energy.

The reciprocity property is illustrated in figure 6. Basically it says that if the sense of the
traveling light is reversed, the value of the BRDF remains unchanged. That is, if the
incoming and outgoing directions are swapped, the value of the BRDF does not change.
Mathematically, this property is written as

The conservation of energy constraint has to do with the scattering of light during the
light-matter interaction. In general, this property states that when light from a single
incoming direction makes contact with a surface and is reflected/scattered over the sphere
of outgoing directions, the total quantity of light that is scattered cannot exceed the
original quantity of light arriving at the surface. Figure 7 illustrates this property. For
each one unit of light energy that arrives at a point, no more than one unit of light energy
can be reflected in total to all possible outgoing directions. By considering the definition
of a BRDF (the ratio of the reflected light to incident light divided by the projected solid
angle), this means the sum over all outgoing directions of the BRDF times the projected
solid angle must be less than one in order for the ratio of the total amount of reflected
light to the incident light to be less than one. Mathematically, this is written as
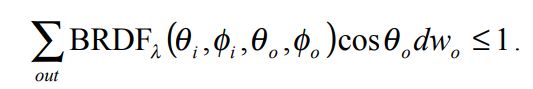
When considering the continuous hemisphere of all outgoing reflected directions, the sum
becomes an integral and this conservation property becomes

the brdf lighting equation
now that we know the definition of a BRDF, we can define a general lighting equation that express how to use BRDFs for computing the illumination produced at a surface point.
suppose we have a scene and we are trying to determine the illumination of a surface point as seen by an observer. in the real-world, the entire environment surrounding a surface in a scene contributes to the illumination of every surface point. this observation can be verified experimentally by examining the appearance of a white sheet of paper
when held next to a green sheet of paper. The reason the color of the green paper appears
to bleed onto the white paper is because the green paper reflects green light – that light in
turn serves as an illumination source for the white paper. In general, any light that arrives
at a surface point from the hemisphere of incoming directions contributes to resulting
illumination.

Figure 8 shows a surface point illuminated by light coming from the surrounding
environment with an observer positioned at the point labeled E. The quantity of light
reflected in the direction of the observer, wo, is a function of all the incoming light and
the BRDF at the surface point. Specifically, when considering the continuous space of
incoming directions, the amount of light reflected in the outgoing direction is the integral
of the amount of light reflected in the outgoing direction from each incoming direction.
That is, the amount of outgoing light, Lo, is given by
For each incoming direction, the amount of reflected light in the outgoing direction is
defined in terms of the BRDF. Suppose that Li is the light intensity incoming from a
specific direction wi. The intensity of the light reflected in the outgoing direction is
defined by modulating the intensity of the light arriving at the surface point with the
corresponding BRDF. Specifically,


In general, interactive computer graphics tends not to consider the entire hemisphere of incoming directions when determining the illumination of a surface. The reason for this is that the math required to compute the lighting equation above is too expensive to compute for more than just a small number of directions. Instead, interactive applications tend to use a small number of individual point light sources to compute the illumination of a surface. Rather than computing a sum of light contributions from many incoming light directions and summing these results to determine the final output color, the small
number of individual point light sources define the set of incoming directions and light
intensities to use in the evaluation of the lighting equation.
For example, suppose that we wish to determine the illumination of a scene containing n
light sources – light source 1 to light source n. In this case, the local illumination of a
surface is given by,


The Phong Lighting Equation
Based upon what we’ve learned about BRDFs, one question that often comes up concerns the relationship between the commonly used Phong lighting model and the general BRDF lighting equation discussed above. To understand where Phong lighting fits in, it’s useful to examine the Phong expression itself. Recall, that Phong lighting relates the amount of light reflected towards a viewer as:

where L is the direction to the light source, V is the direction to the viewer, N is the surface normal, and R is the principle reflection direction. kd and ks are terms used to control the contribution of diffuse and specular components and n is a power term used to
control the width of the specular highlight.
Often, the Phong lighting model includes an ambient term, which approximates global illumination, i.e. multiple inter-reflections of
light before it interacts with the surface point in question. Since this tutorial is concerned with direct illumination, the ambient term has been omitted.
The Phong lighting model can be rewritten as

Notice that this expression looks remarkably similar to the general BRDF lighting
equation for a point light source. If we consider the first fractional term to be a BRDF,
then the Phong lighting model can be looked at as a special case of general BRDF based
lighting. In practice, the Phong model is a computational convenient method to
analytically approximate the reflectance properties of a small set of materials.
Specifically, any materials with reflectance properties that are well approximated by an
analytical function of the form

can be simulated using the Phong model. In general however, not too many materials have reflectance properties of this limited form.
There are also a couple of other small issues with the standard Phong lighting model.
While it’s possible to show that the Phong model is a special case of a BRDF, it is not actually physically plausible because the two physical properties of BRDFs mentioned
earlier do not hold [5]. That is, the standard Phong lighting model is not necessarily energy conserving nor reciprocal. This is not a major issue for local illumination such as
what we are concerned with here, but for global lighting simulations the lack of physical
validity is problematic.
Analytical Models and Acquired BRDF Data
One question that often arises has to do with computing BRDFs for use in the general
BRDF lighting equation. There are actually a couple of different ways to determine the
value of a BRDF. One way is to evaluate mathematical functions derived from analytical
models. The other is by resampling BRDF data acquired by empirical measurements of
real-world surfaces.
Analytical models can be thought of as simple mathematical functions where you plug in
inputs (i.e. direction vectors (θi,φi) and (θo,φo) in addition to other parameters that control
the reflectance properties of the material) and the function computes R, G, and B BRDF
values based on the input parameters. There are actually many simple models that have
been developed that allow for a very wide range of visually interesting lighting effects.
Some examples of these include, the Cook-Torrance model [2], the Modified Phong
model [5], and Ward’s model [7]. In general, different models are useful for modeling
the reflectance characteristics of different types of materials. Ward’s model, for example,
is good at modeling the reflectance properties for surfaces demonstrating a good deal of
anisotropy, such as brushed metal and stringed Christmas tree ornaments. The CookTorrance
model is effective at simulating many types of metals such as copper and gold.
It can also be used for other interesting materials such as plastics with varying degrees of
roughness. In general it is effective for modeling view-dependent changes in color.
In contrast to analytical models, BRDFs can be obtained through physical measurements
made with BRDF measuring devices such as a gonioreflectometer – a device for
measuring the BRDF of a material. Data produced in this way is often referred to as
acquired BRDF data. The advantage of using acquired BRDF data is that many realworld
BRDFs cannot be modeled easily using mathematical models. By using real data,
there is no need to try to determine which analytical model to use to achieve a certain
visual lighting effect. Instead, it’s possible, for example, to measure car paint in the realworld,
and directly use the reflectance data in lighting calculations. Several academic
institutions as well as a few commercial companies offer libraries of measured BRDF
data at little or no cost. Additionally, some companies will actually measure specific data
to meet individual customer needs.
Summary/Conclusion
This paper has presented some of the basic terminology and concepts about BRDFs and
BRDF-based lighting. While it has been somewhat theoretical at times, there are few
pieces of key information that are important to understand for real-time implementations
of BRDF-based lighting. These key pieces of information are:
- Terminology (incoming/outgoing direction)
- Spherical Coordinates (how to move between coordinate spaces)
- Conceptual BRDF Definition (tells reflectance for incoming/outgoing directions)
- Properties of BRDFs (reciprocity and conservation)
- The dynamic range of BRDFs (BRDFs not necessarily limited to [0,1] range)
- The BRDF general lighting equation
- Phong Lighting (why it is limited and why general BRDF-based lighting is better)
- BRDF Models (the difference between analytical models and acquired data sets)
Although it was not explicitly discussed in this tutorial, several practical techniques exist
for doing real-time BRDF based lighting on NVIDIA hardware. Stay tuned for future
tutorials that explain how to use NVIDIA hardware (and other hardware too) to achieve
cool BRDF lighting effects.
References
- Michael F. Cohen and John R. Wallace. Radiosity and Realistic Image Synthesis.
Academic Press, 1993. - Robert Cook and Kenneth Torrance. A reflectance model for computer graphics.
Computer Graphics (Proceedings of SIGGRAPH 81), pages 244-253, 1981. - James D. Foley, Andries van Dam, Steven K. Feiner, and John F. Hughes. Computer
Graphics: Principles and Practice. Addison-Wesley, second edition, 1990. - Andrew Glassner. Principles of Digital Image Synthesis. Morgan Kaufmann, 1995.
- R. Lewis. Making Shaders More Physically Plausible. In Eurographics Workshop
on Rendering, pages 47-62, June 1993. - J. Kautz and M. McCool. Interactive Rendering with Arbitrary BRDFs using
Separable Approximations. 10th Eurographics Rendering Workshop, 1999. - Gregory J. Ward. Measuring and Modeling Anisotropic Reflection. SIGGRAPH ’92,
pages 265-272.


