xgboost算法详细介绍(通过简单例子讲述)
xgboost算法详细介绍(通过简单例子讲述)
- boost算法简介
- 集成学习的任务
- XGBoost简介
- XGBoost的思想
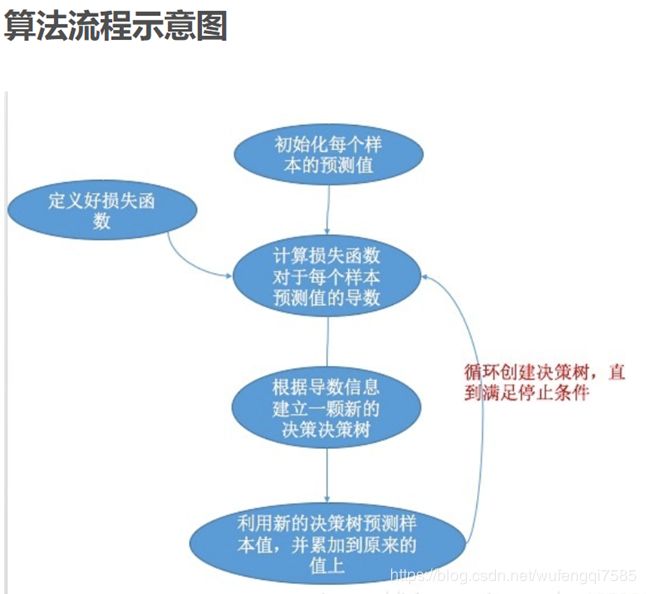
- 通过算法流程图举一个例子详解xgboost树的生成
- 1.首先我们初始化三个样例的考试成绩预测值为0,属性为(天赋高、不恋爱、每天学习时间有16个小时),(天赋低、不恋爱、每天学习时间有16个小时),(天赋高、不恋爱、每天学习时间有6个小时),真实成绩分别为100,70,86分。
- 3.计算损失函数对于每个样本预测值的导数
- 4.根据导数的信息建立一颗新的决策树
- 5.利用新的决策树预测样本值,并累加到原来的值上
- xgboost的简单应用:根据诊断措施预测糖尿病的发病(Kaggle竞赛 )
作者才疏学浅,如有错误还请指正,谢谢!
boost算法简介
Boost 是一种将弱分离器??(?)组合起来形成强分类器 F(?) 的算法框架
“弱分类器”的分类能力不强,但它又比随机选的效果稍微好点,类似于“臭皮匠”。
“强分类器”具有很强的分类能力,也就是把特征扔给它,他能分的比较准确,算是“诸葛亮”一类的。
如果直接可以建立一个强分类器,那弱分类器实际上就是多余的,但是,这世上“绝顶聪明的诸葛亮”少之又少,反而,在某方面有才华的人很多。于是,Boost选择了用三个臭皮匠去顶诸葛亮。
集成学习的任务
集成学习的主要手段就是反复训练多个模型,并将这些模型通过一定方式组合在一起,形成一个高性能的强大的集成模型。在Boosting算法体系中一般采用迭代串行的形式生成一系列模型,然后将这些模型进行线性加权相加,得到最终集成学习器。假设已经迭代到m-1次,得到的集成模型为
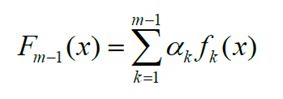
在下一次迭代中,我们要训练,它应该是让新生成的集成模型在训练集上损失最小的模型
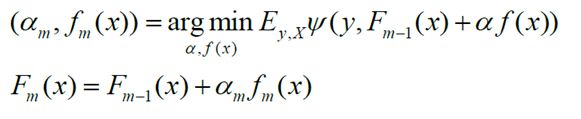
XGBoost简介
xgboost 的全称是eXtreme Gradient Boosting,由华盛顿大学的陈天奇博士提出,在Kaggle的希格斯子信号识别竞赛中使用,因其出众的效率与较高的预测准确度而引起了广泛的关注。
XGBoost的思想
如果boost算法每一步的弱预测模型生成都是依据损失函数的梯度方向,则称之为梯度提升(Gradient boosting),XGBoost算法是采用分步前向加性模型,只不过在每次迭代中生成弱学习器后不再需要计算一个系数,模型形式如下:
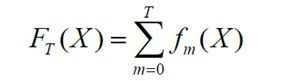
XGBoost算法通过优化结构化损失函数(加入了正则项的损失函数,可以起到降低过拟合的风险)来实现弱学习器的生成,并且XGBoost算法没有采用搜索方法,而是直接利用了损失函数的一阶导数和二阶导数值,并通过预排序、加权分位数等技术来大大提高了算法的性能。
通过算法流程图举一个例子详解xgboost树的生成
我们举一个预测学生考试分数的例子,给定若干个学生属性(比如天赋,每天学习时间,是否恋爱等),通过一个决策树A,我们可以看到,一个通过天赋属性的预测结果:天赋高的人分数+90,天赋低的人+60,通过一个决策树B,可以看到每天学习时间<10小时会使得考试分数收到-5的影响,但是影响不大,以此类推可以通过学生的属性推断其分数情况。XGboost就是这样一个不断生成新的决策树A,B,C,D…的算法,最终生成的决策树算法就是树A+B+C+D+…的和的决策树。
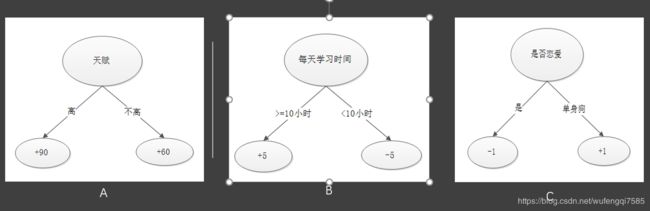
1.首先我们初始化三个样例的考试成绩预测值为0,属性为(天赋高、不恋爱、每天学习时间有16个小时),(天赋低、不恋爱、每天学习时间有16个小时),(天赋高、不恋爱、每天学习时间有6个小时),真实成绩分别为100,70,86分。

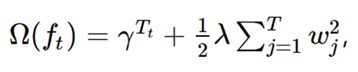
其中Tt为叶结点数,wj为j叶子结点权重,?和λ为预先设计超的参数。
在引入了正则化项后,算法会选择简单而性能优良的模型,损失函数中右端的正则化项
只是用来在每次迭代中抑制弱学习器 fi(x)过拟合的,并不参与最终模型的集成。另外XGBoost 要求L函数至少是二阶连续可导的凸函数。
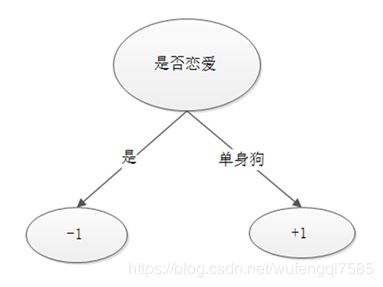
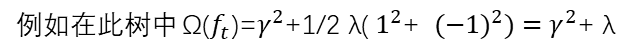
Xgboost系统的每次迭代都会构建一颗新的决策树,决策树通过与真实值之间残差来构建,(天赋高、不恋爱、每天学习时间有16个小时)的大学霸考了100分,(天赋低、不恋爱、每天学习时间有16个小时)的小学霸考了70分,(天赋高、不恋爱、每天学习时间有6个小时)的小天才考了86分,那么三位同学通过第一个决策树后预测结果分别为90分,60分,和90分,在构建第二颗决策树时就会考虑残差(100-90=10),(70-60)=10,(86-90=-4)来构建一颗新的树(具体建树过程之后会讲到),我们通过最小化残差学习到一个通过学习时间属性来构建的决策树的得到90+5,60+5,90-5的预测值,再继续通过(100-95=5)(70-65)(86-85)的残差构建下一个决策树,以此类推,当迭代次数达到上限或是残差不再减小是停止,就得到一个拥有多个(迭代次数)决策树的强分类器。当然分类器是需要考虑更多样本的,我们可以把新加入的决策树fi(x)看作是在N维空间(因为有N个样本)中p(m)相对于点p(m-1)的增量。
当然怎样得到一颗新的树呢?接着看第三个步骤
3.计算损失函数对于每个样本预测值的导数
为什么要计算导数信息呢? ——XGBoost的精髓所在下面我们看一个关于目标函数的简单等式变换:
目标函数: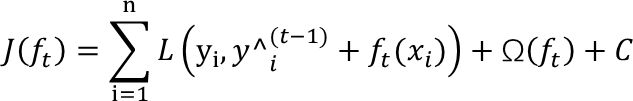
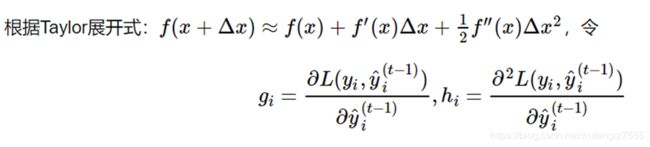

我们可以看到目标函数就这样被转换成了关于g_i和h_i的函数,最终的目标函数只依赖于每个数据点的在误差函数上的一阶导数和二阶导数。这么写的原因很明显,由于之前的目标函数求最优解的过程中只对平方损失函数时候方便求,对于其他的损失函数变得很复杂,通过二阶泰勒展开式的变换,这样求解其他损失函数变得可行了。所以 XGBoost 是直接先求损失函数在该点处的泰勒近似值,然后通过最小化该近似损失函数值来训练弱学习器?? (??)。
4.根据导数的信息建立一颗新的决策树
这里求导数的的过程或者说求导的意义让笔者‘百思不得其解’,因为树模型是阶跃的,阶跃点是不可导的,所以求导就没意义了。
之后笔者查阅了xgboost的源代码,发现源代码对优化函数求导使用了一个简便的算法代替:
def log_reg(y_hat ,y):
p = 1.0/(1.0+ np.exp(-y_hat))
g = p – y.get_lable()
h= p * (1.0-p)
return g,h
就是这么简单~~
所以树模型(回归树)可以通过导数信息寻找最优分裂点。
怎样通过导数建立树呢,我们可以把目标函数进行如下改写,其中j被定义为每个叶子上面样本集合。它将一个样本x 映射到一个相对应的叶子节点,那么可以写成如下形式
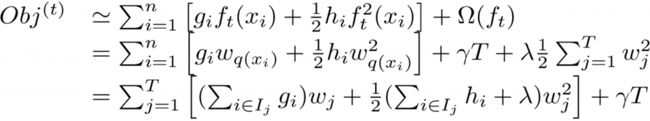
这一个目标包含了个相互独立的单变量二次函数。我们可以定义
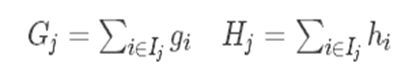
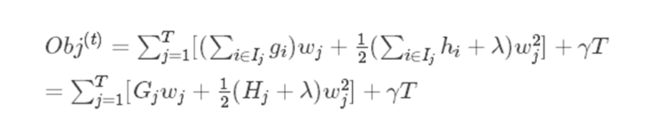
wj就是新建立的树叶子的权值,通过计算对w求偏导=0得:
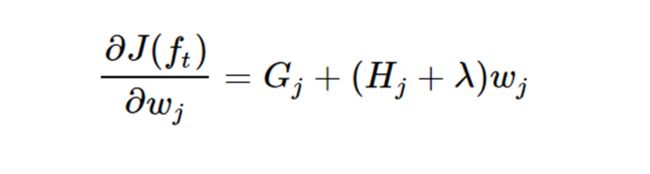
带入目标函数得:

假设我们从一个初始的节点(根节点)开始, I 表示该节点上所有样本的索引集,现在我们要对该节点进行分裂,设 IL,IR分别为分裂后左右子节点中样本的索引集,并且有I=IL∪IR 。那么根据上式我们可以计算出分裂前后第 m个树模型的损失函数值减小量为
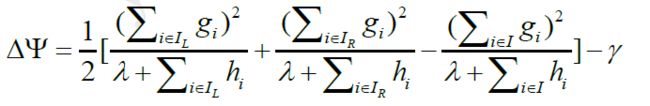
这个公式跟我们决策树算法遇到的信心增益或基尼值增量的公式是一个道理。XGBoost 就是利用这个公式计算出的值作为分裂条件,在每一个节点的分裂中寻找最优的分裂和属性和分裂点。这样我们就能顺利地得到我们在第m 轮迭代中所需要的最优的模型fm(x)。
设有ABCDE五个学生,学习时间分别为16,12,8,6,4小时,通过计算不同分割方法的增益值来确定哪个分割是否是最优分割。我们生成如下一个决策树,决策树的增益值就是通过带入p = 1.0/(1.0+ np.exp(-y_hat)); g = p – y.get_lable();h= p * (1.0-p),计算每个节点的gi和hi,带入如下信息增益公式。注意引入的分割带来的增益小于一个阀值的时候,我们可以剪掉这个分割。
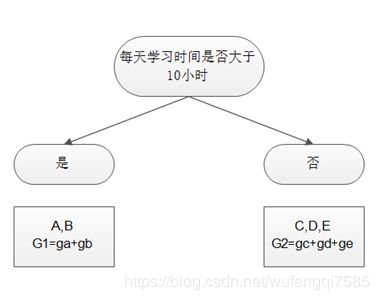
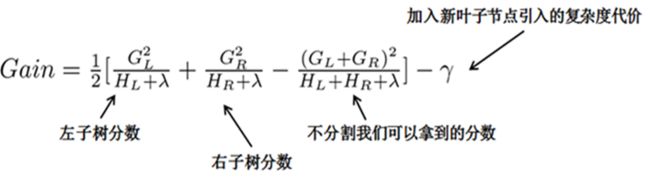
5.利用新的决策树预测样本值,并累加到原来的值上
xgboost的简单应用:根据诊断措施预测糖尿病的发病(Kaggle竞赛 )
数据集有如下几个属性:
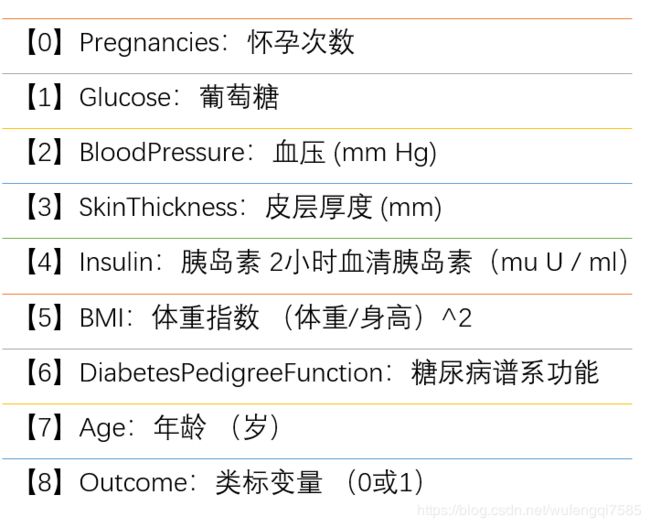
部分数据集如下:
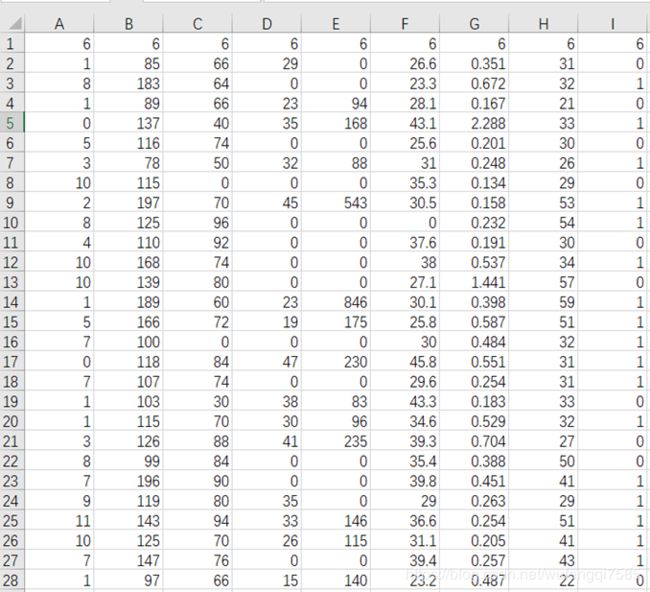
代码如下(数据pima-indians-diabetes.csv可以在网上下载)
from numpy import loadtxt
from xgboost import XGBClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from xgboost import plot_importance
from matplotlib import pyplot
dataset = loadtxt('pima-indians-diabetes.csv', delimiter=",")
X = dataset[:,0:8]
Y = dataset[:,8]
seed = 7
test_size = 0.33
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=test_size, random_state=seed)
model = XGBClassifier()
eval_set = [(X_test, y_test)]
model.fit(X_train, y_train, early_stopping_rounds=10, eval_metric="logloss", eval_set=eval_set, verbose=True)
y_pred = model.predict(X_test)
predictions = [round(value) for value in y_pred]
accuracy = accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))
model.fit(X, Y)
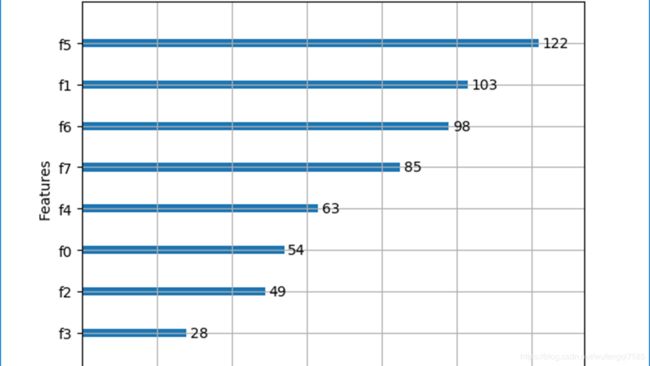
plot_importance(model)
pyplot.show()