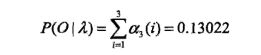HMM解读
HMM的三个基本问题:
Problem 1 (Likelihood): Given an HMM λ = (A,B) and an observation sequence O, determine the likelihood P(O|λ).
Problem 2 (Decoding/Prediction): Given an observation sequence O and an HMM λ = (A,B), discover the best hidden state sequence Q.
Problem 3 (Learning): Given an observation sequence O and the set of states in the HMM, learn the HMM parameters A and B.
Markov chain: 马尔科夫链: 为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质:下一状态的概率分布只能由当前状态决定,在时间序列中他前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔科夫性质。
在 Markov chain 的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。状态的改变叫做转移,与不同的状态改变相关的概率叫做 转移概率。
HMM: 是关于时序的概率模型,描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。 HMM随机生成的状态的序列,成为状态序列(state sequence);每个状态生成一个观测,而由此产生的观测的随机序列,成为观测序列(observation sequence).序列的每一个位置又可以看作是一个时刻。
总结:首先它是一个过程。HMM 生成 state sequence(不可观测的random sequence) 生成 observation sequence(每一个 状态产生一个 观测,由于state是随机的,故而 观测序列也是随机的)
HMM:初始状态概率分布(∏),状态转移概率分布(A)以及观测概率分布(B)
由一个向量和两个矩阵 描述的HMM对于实际系统有着巨大的价值,虽然 经常只是一种近似,但他们却是经得起分析的。HMM通常解决的问题包括:
- 对于一个观察序列 匹配最可能的系统----评估,使用 前向算法(forwward algorithm)解决
- 对于已生成的一个观察序列,确定最可能的隐藏状态序列—解码/预测,使用Viterbi算法解决
- 对于已生成的观察序列,决定最可能的模型参数—学习,有监督(利用频率代替概率)和无监督(Baum-Welch算法)
前向算法:
利用动态规划的思想,进行递推,
前向概率: 时刻t时,隐藏状态状态为qi ,观测状态序列为 O1,O2,…Ot的概率为 前向概率,记为
则t+1时刻,对应的隐藏状态为i的前向概率 为:
解释说明:
at+1(i)指明是 t+1时刻,隐藏状态为 i,观测序列为 O1,O2,…Ot+1 的前向概率
at(j)*aji :前半部分意思是 t时刻,状态为j的前向概率,aji 意思是由状态j转移至状态i的转移概率。
j=1N![]() at(j)*aji 意思是 转移至 当前 状态i有N中方式,故而状态i的概率为 N种方式的和。此整体可以理解为 t+1时刻状态为i的概率
at(j)*aji 意思是 转移至 当前 状态i有N中方式,故而状态i的概率为 N种方式的和。此整体可以理解为 t+1时刻状态为i的概率
Bi(Ot+1) 意思是t+1时刻,由 状态i得到观测Ot+1的概率。
具体算法流程如下
以下面例子说明:
如上图所示,先求t=1时刻,前向概率为
a1(i)=∏ibi(O1) i=1,2,3
分别求得 在状态 i=1,2,3状态下的前向概率
T=2:
由于t=1时刻,各个状态的前向概率已经求得,故而直接带入公式即可,如上图所示。
依次类推,即可求得a3(i), i=1,2,3
后向算法:
后向算法与前向算法思想都一致,只不过方向 相反而已,只要 读懂 每个变量 是什么意思,即可明白,下面是 李航 老师 的 截图,自己看一下 就 ok了
学习算法: 直接 看 李航 老师 的 pdf即可
预测算法:
近似算法:
维特比算法(viterbi algorithm):
用动态规划求概率最大路径(最优路径),这时一条路径对应着一个状态序列。
即 认为 t+1时刻的最优路径是基于t时刻的路径也为最优,
对上述变量的解释:
- 公式10.44意思是 在时刻t, 状态为 i,且 观测为 O1,O2,…Ot 的概率中最大的,因为 根据状态转移矩阵可知, t时刻,到达状态i的路径有很多种(从t-1时刻的j状态,s.t. 1<=j<=N, 共N个状态而来),故而需要获取 最优值,也即概率最大值
- 公式 10.45 中 中括弧 意思是,在t时刻,状态为j 的最大概率 路径,转移至 t+1时刻 i状态的概率。整个公式的意思是 t+1时刻状态 为i且 在t+1时刻 i状态下 观测是 Ot+1 的最大概率
- 公式 10.46 意思是,获取 时刻t,概率最大 路径 的 第t-1个状态索引(状态节点)
下面是李航 老师 对viterbi算法的概述:
知乎: https://zhuanlan.zhihu.com/albertwang
微信公众号:AI-Research-Studio
![]()
下面是赞赏码