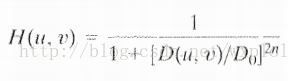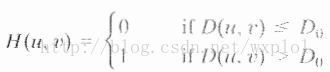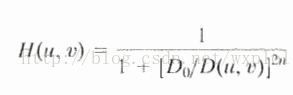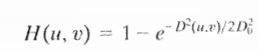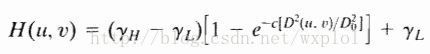图像增强之频域增强

一、傅里叶变换

关于傅里叶变换等基础知识这里就不一一解释，网上有好多，自己可以百度。

二、图像处理中的二维离散傅里叶变换

我们知道二维图像的傅里叶变换可以用以下数学公式：

表示变换后的结果需要用实数图和虚数图表示（或幅值图和相位图）。

三、频域滤波基础

    傅里叶变换在图像处理中可以做到图像的增强以及去噪、图像的分割之边缘检测、图像的特征提取和图像压缩，本节中主要

讲一些图像增强的内容，其他方面可以看我相关的其他博客。

    在频域中高频代表了图像的边缘或者纹理细节，而低频代表了图像的轮廓信息，所以，和空间域滤波类似，低通滤波可

以看做对图像的模糊，而高通滤波器可以看做边缘检测。

同时，频率的变化快慢也与图像的平均灰度成正比。低频对应于图像中缓慢变换的灰度分量，高频对应于灰度变换快的

分量。

    因此，我们可以用这样一个在频域的滤波器来过滤频域中的高频或者低频部分，在将频域中图像傅里叶反变换转换到空

间域实现图像的增强功能。其具体的实现如下：

（1）给定一个大小为MXN的输入图像，同时由式：p>=2M-1;Q>=2N-1，得到填充数据P和Q。（一般p=2M,Q=2N）；

（2）对f（x,y）添加一定数量的0进行边界扩充（注意此时图像位于左上角），形成PXQ的图像fp(x,y)；

（3）用（-1）^x+y乘以fp(x,y)使其变换到图像的中心位置（注意opencv中处理于此种方法不同，具体参考我的相关博客）；

（4）计算fp(x,y)的傅里叶变换得到F(u,v)；

（5）生成一个实的、对称的滤波函数G(u,v)大小与PXQ，中心在（P/2,Q/2）处。用阵列相乘G(u,v)=H(u,v)F(u,v)（注意频域的

乘积相当于空间域的卷积）；

（6）将相乘后的结果转换到空间域中

四、平滑图像

由上一节可知，平滑图像需要用到低通滤波器，下面主要将一些常见的低通滤波器。

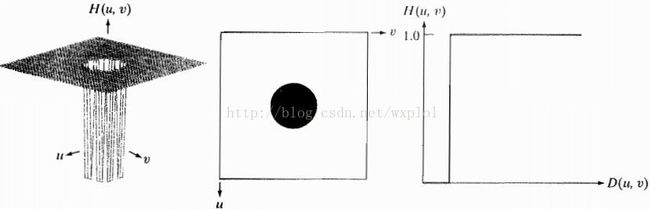
（1）理想低通滤波器（ILPF）

如上图所示，ILPF的截止频率为D0,其基本的函数为：

 

（2）布沃斯低通滤波器（BLPF）

 

其基本函数为：

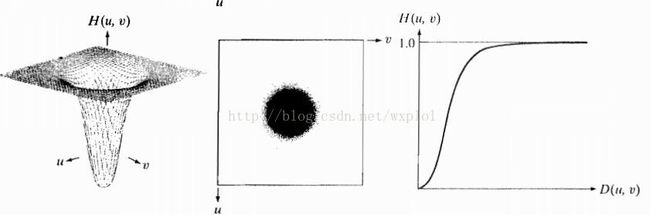
（3）高斯低通滤波器

其函数为：

五、锐化图像

（1）理想高通滤波器

（2）布沃斯高通滤波器

（3）高斯高通滤波器

（4）拉普拉斯算子

（5）钝化、高提升滤波和高频强调滤波

（6）同态滤波

一幅图像可以表示为照射变量i(x,y)和反射变量r(x,y)的乘积,如下

图像的照射分量通常由慢的控空间变化表征，而反射分量往往引起突变，所以，图像傅里叶变换后的低频成分与照射想联系

而高频部分与反射相联系。其滤波器如下图：

函数为：

通过设置rH和rL来控制低频或高频的衰减，其最终效果是同时进行动态范围的压缩和对比度的增强。同态滤波的处理过程如下图：

六、选择性滤波

（1）带阻滤波和带通滤波

（2）陷波滤波器