Brian2学习笔记二 Introduction to Brian part 2:Synapses
Brian2学习笔记二 Introduction to Brian part 2 :Synapses
- 1. 前言
- 2. 正文
- 2.1 最简单的突触(The simplest Synapse)
- 2.2 加入权重(Adding a weight)
- 2.3 引入时滞(Introducing a delay)
- 2.4 更复杂的连接(More complex connectivity)
- 2.1 更复杂的突触模型:STDP(More complex synapse models: STDP)
1. 前言
推荐几个CSDN上不错的类似教程:
1、链接: https://blog.csdn.net/u013751642/article/details/80932308.
2、链接: https://blog.csdn.net/lemonade_117/article/details/81145881.
3、链接: https://blog.csdn.net/xiaoqu001/article/details/80422546#_Tutorial_84.
上一篇文章介绍了神经元,在生物中,神经元是通过突触连接的,前向神经元通过突触将电流信息传递给后向神经元,突触的类型又分为电突触和化学突触,不同类型的突触可以改变神经元的发放电状态,这也是神经网络的基础。
那么在本次教程中,我们就主要来介绍突触相关的内容,本文是根据Brian2官网提供的英文教程进行翻译整理总结的。
Brian2的官方安装教程链接:
链接: https://brian2.readthedocs.io/en/stable/introduction/install.html.
官方文档链接及Jupyter notebook学习资料:
链接: https://brian2.readthedocs.io/en/stable/resources/tutorials/2-intro-to-brian-synapses.html.
(注意:本文所有代码运行环境为Anaconda 的 Spyder(python 3.6), 注意运行代码首先要通过如下代码来导入 Brian2的包)

2. 正文
2.1 最简单的突触(The simplest Synapse)
首先,我们定义了神经元以后,接下来就要通过突触来连接它们,那么,我们将会介绍一个最简单的突触,它在一个脉冲之后会产生变量的瞬时改变,代码如下:
from brian2 import *
start_scope()
eqs = '''
dv/dt = (I-v)/tau : 1
I : 1
tau : second
'''
G = NeuronGroup(2, eqs, threshold='v>1', reset='v = 0', method='exact')
G.I = [2, 0]
G.tau = [10, 100]*ms
# Comment these two lines out to see what happens without Synapses
S = Synapses(G, G, on_pre='v_post += 0.2')
S.connect(i=0, j=1)
M = StateMonitor(G, 'v', record=True)
run(100*ms)
plot(M.t/ms, M.v[0], label='Neuron 0')
plot(M.t/ms, M.v[1], label='Neuron 1')
xlabel('Time (ms)')
ylabel('v')
legend()
运行结果如下:
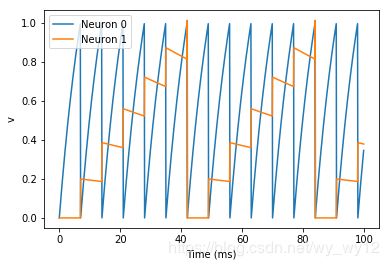
在这里我们需要说明以下几点:首先,在本例中,我们再来看NeuronGroup做了什么,它创建了两个神经元,它们用相同的微分方程来表示,但是变量 I I I 和 t a u tau tau 的值不同。神经元Neuron0的变量 I = 2 , t a u = 10 ∗ m s I=2,tau=10*ms I=2,tau=10∗ms, 这表示它可以以一个更高的比率重复发放脉冲。神经元Neuron1的变量 I = 0 , t a u = 100 ∗ m s I=0,tau=100*ms I=0,tau=100∗ms 意味着如果没有与它相连的突触,它将永远不会发放脉冲(刺激电流 I I I 为 0 0 0),你可以通过注释掉突触的两行代码来自己验证一下。
接下来,我们定义了突触:Synapses(source,target,…)意味着我们定义了一个从source到target的突触模型。在本例中,source和target相同,都是G。代码中 on_pre=’v_post+=0.2’意味着当一个脉冲在突触前神经元中产生时,它会瞬时使得后一个神经元产生变化, v_post+=0.2 。符号 _post 意味着v的值是指突触后神经元的值,它会增加0.2 。
所以总的来说,该模型的作用就是:G中的两个神经元通过突触连接时,当source神经元发放一个脉冲时,target神经元的v值将增加0.2。然而,前面我们只是定义了突触的模型,还没有真正地创建任何突触。S.connect(i=0,j=1) 则意味着创建了一个从神经元Neuron0到神经元Neuron1的突触连接。
2.2 加入权重(Adding a weight)
在前文中,我们将突触的权重固定为0.2,但是,通常我们期望不同的突触有不同的权重。接下来我们来引入突触方程。
代码如下:
from brian2 import *
start_scope()
eqs = '''
dv/dt = (I-v)/tau : 1
I : 1
tau : second
'''
G = NeuronGroup(3, eqs, threshold='v>1', reset='v = 0', method='exact')
G.I = [2, 0, 0]
G.tau = [10, 100, 100]*ms
# Comment these two lines out to see what happens without Synapses
S = Synapses(G, G, 'w : 1', on_pre='v_post += w')
S.connect(i=0, j=[1, 2])
S.w = 'j*0.2'
M = StateMonitor(G, 'v', record=True)
run(50*ms)
plot(M.t/ms, M.v[0], label='Neuron 0')
plot(M.t/ms, M.v[1], label='Neuron 1')
plot(M.t/ms, M.v[2], label='Neuron 2')
xlabel('Time (ms)')
ylabel('v')
legend()
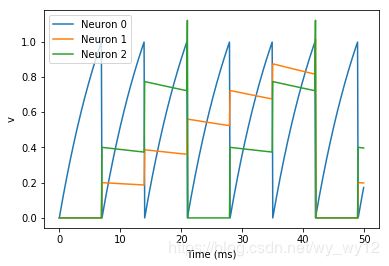
这个例子与前面的例子非常相似,但是多了一个突触权重变量w。字符‘w : 1’也是一个方程,它表示为所有的神经元定义了一个无量纲的参数,我们通过on_pre=’v_post += w’来改变脉冲的行为,使得每个突触基于w的不同而不同。为了说明这一点,我们同时创建了第三个神经元,它的行为与第二个神经元完全相同,并将神经元0分别与神经元1和神经元2连接起来。其中,i 指的是source神经元索引,j指的是target神经元索引,我们也通过S.w = ‘j * 0.2’来设置权重,使得从 0 到 1(j=1)的突触连接权重为 0.2=0.2 * 1,从0 到 2(j=2)的突触连接权重为 0.4=0.2 * 2。
2.3 引入时滞(Introducing a delay)
到目前为止,突触都是即时发生的,但是我们也可以加入一些时滞的延迟:
from brian2 import *
start_scope()
eqs = '''
dv/dt = (I-v)/tau : 1
I : 1
tau : second
'''
G = NeuronGroup(3, eqs, threshold='v>1', reset='v = 0', method='exact')
G.I = [2, 0, 0]
G.tau = [10, 100, 100]*ms
S = Synapses(G, G, 'w : 1', on_pre='v_post += w')
S.connect(i=0, j=[1, 2])
S.w = 'j*0.2'
S.delay = 'j*2*ms'
M = StateMonitor(G, 'v', record=True)
run(50*ms)
plot(M.t/ms, M.v[0], label='Neuron 0')
plot(M.t/ms, M.v[1], label='Neuron 1')
plot(M.t/ms, M.v[2], label='Neuron 2')
xlabel('Time (ms)')
ylabel('v')
legend()
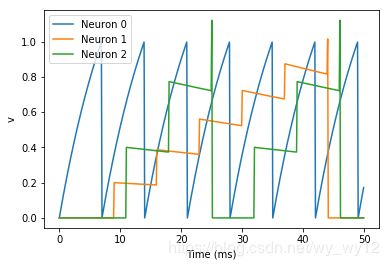
通过上面结果图,我们通过添加了一行S.delay = ‘j * 2 * ms’使得突触从0到1(j=1),S.delay = ‘1* 2 * ms’有2ms的延迟,从0到2(j=2) S.delay = ‘2 * 2 * ms’有4ms的延迟。
2.4 更复杂的连接(More complex connectivity)
到目前为止,我们介绍的突触的连接都是明确的,但是对于更大的网络来说,这通常是无法实现的。基于此,我们通常需要指定一些条件。
start_scope()
N = 10
G = NeuronGroup(N, 'v:1')
S = Synapses(G, G)
S.connect(condition='i!=j', p=0.2)
这里我们创建了含有N个仿真的神经元和一个突触仿真的模型。实际上并没有做任何事情,只是用来说明这种连接。
代码行S.connect(condition=’i!j’, p=0.2)表示只有当 i!j 的条件满足时,就会以 p=0.2 的概率将神经元 i 和神经元 j 相连。那么,我们如何才能看到这种连接呢?这里提供了一个小函数可以让我们将这种连接可视化。执行如下代码。
from brian2 import *
prefs.codegen.target = "numpy" //#use the Python fallback
start_scope()
N = 10
G = NeuronGroup(N, 'v:1')
S = Synapses(G, G)
S.connect(condition='i!=j', p=0.2)
def visualise_connectivity(S):
Ns = len(S.source)
Nt = len(S.target)
figure(figsize=(10, 4))
subplot(121)
plot(zeros(Ns), arange(Ns), 'ok', ms=10)
plot(ones(Nt), arange(Nt), 'ok', ms=10)
for i, j in zip(S.i, S.j):
plot([0, 1], [i, j], '-k')
xticks([0, 1], ['Source', 'Target'])
ylabel('Neuron index')
xlim(-0.1, 1.1)
ylim(-1, max(Ns, Nt))
subplot(122)
plot(S.i, S.j, 'ok')
xlim(-1, Ns)
ylim(-1, Nt)
xlabel('Source neuron index')
ylabel('Target neuron index')
visualise_connectivity(S)
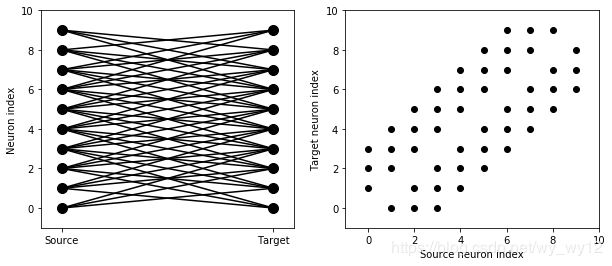
输出结果:
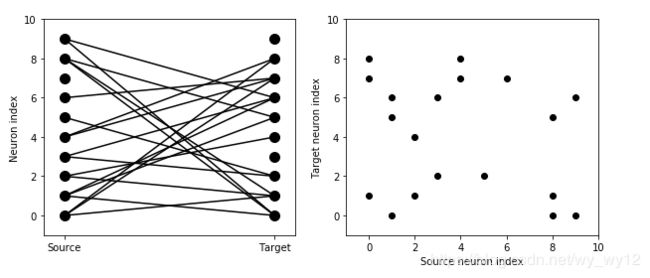
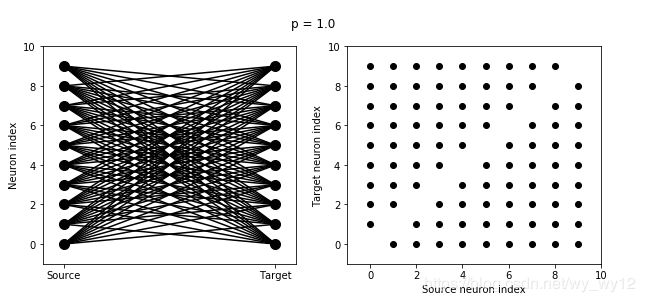
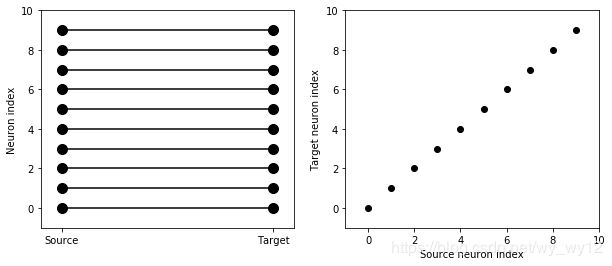
输出结果有两个图。其中,左图的左边垂直排列的10个黑点表示source神经元,右边垂直排列的10个黑点则表示target神经元,两边神经元之间的连线代表这两者之间存在一个突触。右边的图展示的是对这种连接的另外一种表示方式(类似矩阵的表示方式),图中每一个黑点都代表了一个突触,x轴的代表source神经元索引,y轴代表target神经元索引。
需要注意的是:大家发现我们的代码中添加了第二行 prefs.codegen.target = “numpy” //#use the Python fallback ,如果没有这一行,输出结果会是如下:
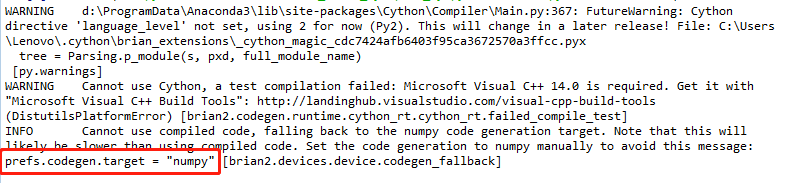
这是用于我们没有安装 Microsoft Visual C++ 14.0 (可以通过Microsoft Visual C++ Build Tools来下载安装),所以不能运行Cython,为了避免这种情况,提示我们加入代码:
prefs.codegen.target = "numpy"
虽然会速度较慢,但是可以编译成功,这也是在运行官方文档的过程中发现的问题。
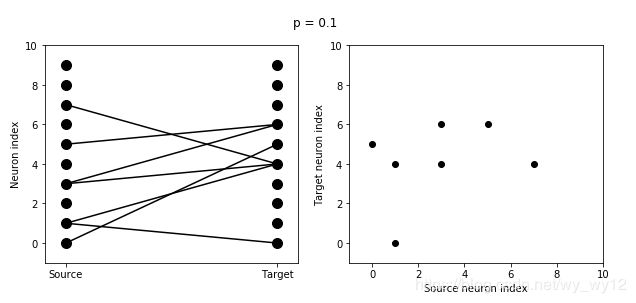
那么接下来,我们来观察一下如果改变连接概率P, 会发生什么变化?
from brian2 import *
prefs.codegen.target = "numpy"
start_scope()
N = 10
G = NeuronGroup(N, 'v:1')
for p in [0.1, 0.5, 1.0]:
S = Synapses(G, G)
S.connect(condition='i!=j', p=p)
visualise_connectivity(S)
suptitle('p = '+str(p))
def visualise_connectivity(S):
Ns = len(S.source)
Nt = len(S.target)
figure(figsize=(10, 4))
subplot(121)
plot(zeros(Ns), arange(Ns), 'ok', ms=10)
plot(ones(Nt), arange(Nt), 'ok', ms=10)
for i, j in zip(S.i, S.j):
plot([0, 1], [i, j], '-k')
xticks([0, 1], ['Source', 'Target'])
ylabel('Neuron index')
xlim(-0.1, 1.1)
ylim(-1, max(Ns, Nt))
subplot(122)
plot(S.i, S.j, 'ok')
xlim(-1, Ns)
ylim(-1, Nt)
xlabel('Source neuron index')
ylabel('Target neuron index')

接下来,我们来观察如果改变连接条件会发生什么?让它们只与相邻的神经元相连
from brian2 import *
prefs.codegen.target = "numpy"
start_scope()
N = 10
G = NeuronGroup(N, 'v:1')
S = Synapses(G, G)
S.connect(condition='abs(i-j)<4 and i!=j')
visualise_connectivity(S)
def visualise_connectivity(S):
Ns = len(S.source)
Nt = len(S.target)
figure(figsize=(10, 4))
subplot(121)
plot(zeros(Ns), arange(Ns), 'ok', ms=10)
plot(ones(Nt), arange(Nt), 'ok', ms=10)
for i, j in zip(S.i, S.j):
plot([0, 1], [i, j], '-k')
xticks([0, 1], ['Source', 'Target'])
ylabel('Neuron index')
xlim(-0.1, 1.1)
ylim(-1, max(Ns, Nt))
subplot(122)
plot(S.i, S.j, 'ok')
xlim(-1, Ns)
ylim(-1, Nt)
xlabel('Source neuron index')
ylabel('Target neuron index')
你也可以通过生成器语法来创建更高效地连接。在上面的小例子中,这并不重要,但是对于数量巨大的神经元网络来说,直接指定哪些神经元应该被连接将远比只指定一个条件有效的多。下面的例子中将使用skip_if_invalid来避免边界错误(例如,不将索引为1的神经元与索引为-2的神经元相连)
from brian2 import *
prefs.codegen.target = "numpy"
start_scope()
N = 10
G = NeuronGroup(N, 'v:1')
S = Synapses(G, G)
S.connect(j='k for k in range(i-3, i+4) if i!=k', skip_if_invalid=True)
visualise_connectivity(S)
def visualise_connectivity(S):
Ns = len(S.source)
Nt = len(S.target)
figure(figsize=(10, 4))
subplot(121)
plot(zeros(Ns), arange(Ns), 'ok', ms=10)
plot(ones(Nt), arange(Nt), 'ok', ms=10)
for i, j in zip(S.i, S.j):
plot([0, 1], [i, j], '-k')
xticks([0, 1], ['Source', 'Target'])
ylabel('Neuron index')
xlim(-0.1, 1.1)
ylim(-1, max(Ns, Nt))
subplot(122)
plot(S.i, S.j, 'ok')
xlim(-1, Ns)
ylim(-1, Nt)
xlabel('Source neuron index')
ylabel('Target neuron index')

那么,如果每个source神经元精确地与一个target神经元相连(通常用于两个大小相同的独立组,而不是本例中完全相同的source和target),那么就会有一种非常高效的特殊语法。例如,1到1连接正是如此
from brian2 import *
prefs.codegen.target = "numpy"
start_scope()
N = 10
G = NeuronGroup(N, 'v:1')
S = Synapses(G, G)
S.connect(j='i')
visualise_connectivity(S)
def visualise_connectivity(S):
Ns = len(S.source)
Nt = len(S.target)
figure(figsize=(10, 4))
subplot(121)
plot(zeros(Ns), arange(Ns), 'ok', ms=10)
plot(ones(Nt), arange(Nt), 'ok', ms=10)
for i, j in zip(S.i, S.j):
plot([0, 1], [i, j], '-k')
xticks([0, 1], ['Source', 'Target'])
ylabel('Neuron index')
xlim(-0.1, 1.1)
ylim(-1, max(Ns, Nt))
subplot(122)
plot(S.i, S.j, 'ok')
xlim(-1, Ns)
ylim(-1, Nt)
xlabel('Source neuron index')
ylabel('Target neuron index')
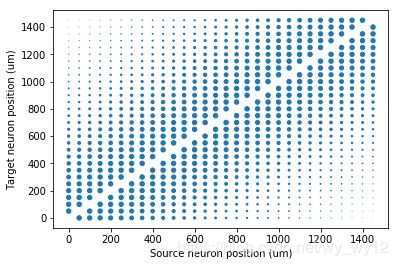
你也可以做一些有趣的事情,比如用一个字符串指定权重的值。让我们来看一个例子,我们为每个神经元分配一个空间位置,并有一个依赖于距离的连接函数。我们通过标记的大小来可视化突触的权重。
from brian2 import *
prefs.codegen.target = "numpy"
start_scope()
N = 30
neuron_spacing = 50*umetre
width = N/4.0*neuron_spacing
# Neuron has one variable x, its position
G = NeuronGroup(N, 'x : metre')
G.x = 'i*neuron_spacing'
# All synapses are connected (excluding self-connections)
S = Synapses(G, G, 'w : 1')
S.connect(condition='i!=j')
# Weight varies with distance
S.w = 'exp(-(x_pre-x_post)**2/(2*width**2))'
scatter(S.x_pre/um, S.x_post/um, S.w*20)
xlabel('Source neuron position (um)')
ylabel('Target neuron position (um)')
def visualise_connectivity(S):
Ns = len(S.source)
Nt = len(S.target)
figure(figsize=(10, 4))
subplot(121)
plot(zeros(Ns), arange(Ns), 'ok', ms=10)
plot(ones(Nt), arange(Nt), 'ok', ms=10)
for i, j in zip(S.i, S.j):
plot([0, 1], [i, j], '-k')
xticks([0, 1], ['Source', 'Target'])
ylabel('Neuron index')
xlim(-0.1, 1.1)
ylim(-1, max(Ns, Nt))
subplot(122)
plot(S.i, S.j, 'ok')
xlim(-1, Ns)
ylim(-1, Nt)
xlabel('Source neuron index')
ylabel('Target neuron index')
2.1 更复杂的突触模型:STDP(More complex synapse models: STDP)
Brian的突触结构是非常常见的,它可以实现类似短期可塑性(STP)或脉冲时间依赖可塑性(STDP)。接下来我们看一下如何实现STDP。
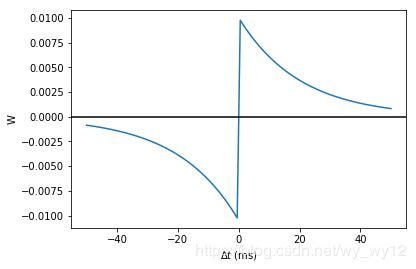
STDP通常定义如下方程所示:
Δ w = ∑ t p r e ∑ t p o s t W ( t p o s t − t p r e ) \Delta w=\sum_{t_{pre}}\sum_{t_{post}}W(t_{post}-t_{pre}) Δw=∑tpre∑tpostW(tpost−tpre)
也就是说,突触权重w的变化是所有突触前脉冲发放时间 t p r e t_{pre} tpre 和突触后脉冲发放时间 t p o s t t_{post} tpost 差的某一W函数的总和。常用的W函数为:
W ( Δ t ) = { A p r e e − Δ t / τ p r e , Δ t > 0 A p o s t e Δ t / τ p o s t , Δ t < 0 W(\Delta t)= \begin{cases} & A_{pre} e^{-\Delta t/\tau _{pre}} , \Delta t>0 \\ & A_{post} e^{\Delta t/\tau _{post}},\Delta t<0 \end{cases} W(Δt)={Apree−Δt/τpre,Δt>0AposteΔt/τpost,Δt<0
以下为函数代码:
from brian2 import *
prefs.codegen.target = "numpy"
start_scope()
tau_pre = tau_post = 20*ms
A_pre = 0.01
A_post = -A_pre*1.05
delta_t = linspace(-50, 50, 100)*ms
W = where(delta_t>0, A_pre*exp(-delta_t/tau_pre), A_post*exp(delta_t/tau_post))
plot(delta_t/ms, W)
xlabel(r'$\Delta t$ (ms)')
ylabel('W')
axhline(0, ls='-', c='k')
运行结果:
直接用上述方程来模拟它将是非常低效的,因为我们需要对所有的脉冲进行求和,这在生理学上也是不现实的,因为神经元不可能记住它之前所有的脉冲的发放时间。我们需要一种更叫高效合理的方法来获得同样的效果。
我们定义了两个新的变量 a p r e a_{pre} apre和 a p o s t a_{post} apost,它们是突触前和突触后活动的“trace”,并通过微分方程来控制。
τ p r e d d t a p r e = − a p r e \tau _{pre}\tfrac{d}{dt}a_{pre}=-a_{pre} τpredtdapre=−apre
τ p o s t d d t a p o s t = − a p o s t \tau _{post}\tfrac{d}{dt}a_{post}=-a_{post} τpostdtdapost=−apost
当一个突触前脉冲出现的时候,突触前跟踪器和权重将会被更新。
a p r e → a p r e + A p r e a_{pre}\rightarrow a_{pre}+A_{pre} apre→apre+Apre
w → w + a p o s t w\rightarrow w+a_{post} w→w+apost
当一个突触后神经元脉冲出现时:
a p o s t → a p o s t + A p o s t a_{post}\rightarrow a_{post}+A_{post} apost→apost+Apost
w → w + a p r e w\rightarrow w+a_{pre} w→w+apre
为了验证这个策略的对等性,你只需要检查方程的和是否是线性的,同时考虑两种情况:如果突触前神经元在突触后神经元之前放电会发生什么?反之亦然,也可以试着画图来观察。
现在我们有了一个只依赖于微分方程和脉冲事件的公式,我们可以将其转换成Brian2的代码:
from brian2 import *
prefs.codegen.target = "numpy"
start_scope()
taupre = taupost = 20*ms
wmax = 0.01
Apre = 0.01
Apost = -Apre*taupre/taupost*1.05
G = NeuronGroup(1, 'v:1', threshold='v>1')
S = Synapses(G, G,
'''
w : 1
dapre/dt = -apre/taupre : 1 (event-driven)
dapost/dt = -apost/taupost : 1 (event-driven)
''',
on_pre='''
v_post += w
apre += Apre
w = clip(w+apost, 0, wmax)
''',
on_post='''
apost += Apost
w = clip(w+apre, 0, wmax)
''')
这里需要说明以下几点:
首先,当我们定义突触时,用复杂的多行字符串给出了三个突触变量(w,apre和apost)。在apre和apost定义之后,我们也得到了一个新的语法(事件驱动)。也就是说,尽管这两个变量随着时间不断变化,但Brian只在一个事件(一个脉冲)发生时更新它们。因为对于对于脉冲生成时刻之外的apre和apost的值我们是不需要的,只在需要的时候才更新它们,这样才会效率更高。
接下来我们有一个on_pre=…参数。
第一行代码:v_post += w实际应用在与target神经元相连的突触权重。
第二行代码:apre += Apre编码了上面的规则。
第三行代码,我们也编码了上面的规则,但是我们增加了一个新的特征,我们把突触的权值设置在最小值0和最大值wmax之间,这样权值就不会太大或者是负的,并用函数clip(x,low,high)来实现这个功能。
最后,我们有一个on_post=…参数。这给出了当突触后神经元发放时的计算。注意,在这种情况下不修改v,只修改突触变量。
现在让我们看一下当突触前脉冲先于突触后脉冲到达时所有变量将如何变化:
from brian2 import *
prefs.codegen.target = "numpy"
start_scope()
taupre = taupost = 20*ms
wmax = 0.01
Apre = 0.01
Apost = -Apre*taupre/taupost*1.05
G = NeuronGroup(2, 'v:1', threshold='t>(1+i)*10*ms', refractory=100*ms)
S = Synapses(G, G,
'''
w : 1
dapre/dt = -apre/taupre : 1 (clock-driven)
dapost/dt = -apost/taupost : 1 (clock-driven)
''',
on_pre='''
v_post += w
apre += Apre
w = clip(w+apost, 0, wmax)
''',
on_post='''
apost += Apost
w = clip(w+apre, 0, wmax)
''', method='linear')
S.connect(i=0, j=1)
M = StateMonitor(S, ['w', 'apre', 'apost'], record=True)
run(30*ms)
figure(figsize=(4, 8))
subplot(211)
plot(M.t/ms, M.apre[0], label='apre')
plot(M.t/ms, M.apost[0], label='apost')
legend()
subplot(212)
plot(M.t/ms, M.w[0], label='w')
legend(loc='best')
xlabel('Time (ms)')
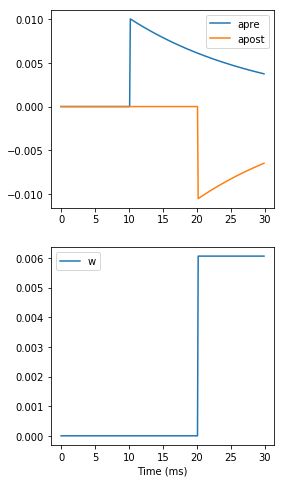
有几点需要注意:
首先,我们使用了一个小技巧,让神经元0在10ms时发放一个脉冲,而让神经元1在20ms时发放一个脉冲。你能看出它们是如何工作的吗?
其次,我们已经用clock_driven替换了event_driven,这样你就可以看到apre和apost是如何随着时间变化的。试着改变脉冲发放时间,看看会发生什么。
最后,我们来验证一下这个公式是否和原始的公式等价。
from brian2 import *
prefs.codegen.target = "numpy"
start_scope()
taupre = taupost = 20*ms
Apre = 0.01
Apost = -Apre*taupre/taupost*1.05
tmax = 50*ms
N = 100
# Presynaptic neurons G spike at times from 0 to tmax
# Postsynaptic neurons G spike at times from tmax to 0
# So difference in spike times will vary from -tmax to +tmax
G = NeuronGroup(N, 'tspike:second', threshold='t>tspike', refractory=100*ms)
H = NeuronGroup(N, 'tspike:second', threshold='t>tspike', refractory=100*ms)
G.tspike = 'i*tmax/(N-1)'
H.tspike = '(N-1-i)*tmax/(N-1)'
S = Synapses(G, H,
'''
w : 1
dapre/dt = -apre/taupre : 1 (event-driven)
dapost/dt = -apost/taupost : 1 (event-driven)
''',
on_pre='''
apre += Apre
w = w+apost
''',
on_post='''
apost += Apost
w = w+apre
''')
S.connect(j='i')
run(tmax+1*ms)
plot((H.tspike-G.tspike)/ms, S.w)
xlabel(r'$\Delta t$ (ms)')
ylabel(r'$\Delta w$')
axhline(0, ls='-', c='k')