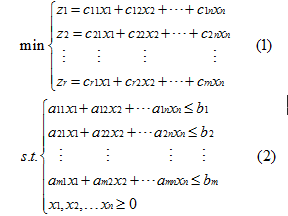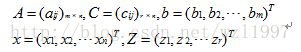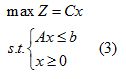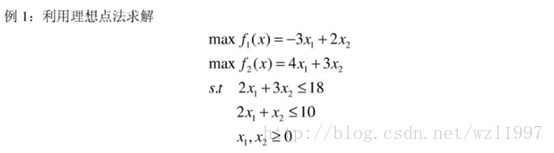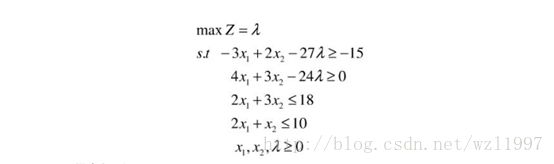多目标线性规划求解方法及matlab实现

求解多目标线性规划的基本思想是将多目标转化为单目标，常见的方法有理想点法、线性加权法、最大最小法、目标规划法、模糊数学解法等。这里就这几种方法进行举例说明，并用matlab实现。

 

一、多目标线性规划模型

多目标线性规划模型是有两个或两个以上的目标函数，且所有的目标函数和约束条件都是线性的，数学模型表示为：

 

我们记

 

则上述目标规划可简化为：

 

 

 

二、MATLAB优化工具箱常用函数

常用的求解最优化问题的函数，有线性规划问题的linprog，非线性规划问题的fmincon，最大最小问题的fminimax，求解多目标的fgoalattain等。调用形式分别为：

 

 

 

三、多目标线性规划的求解方法及MATLAB实现

1.理想解法：

 

 

 

解：先对单目标进行求解

对第一个目标求解的matlab程序为：

 

f=[3;-2];
a=[2  3;2 1];
b=[18;10];
lb=[0;0];
ub=[];
[x,favl]=linprog(f,a,b,[],[],lb,ub);

 

输出结果为：x=0.0000 6.0000，favl=-12.0000，所以最大值为12.0000

对第二个目标求解的matlab程序为：

 

f=[-4;-3];
a=[2  3;2 1];
b=[18;10];
lb=[0;0];
ub=[];
[x,favl]=linprog(f,a,b,[],[],lb,ub);

 

输出结果为：x=3.0000 4.0000，favl=-24.0000，所以最大值为24.0000

于是得到理想点：（12,24）

 

Matlab程序为：

 

x0=[1;1];
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
ub=[];
x=fmincon('((-3*x(1)+2*x(2)-12)^2+(4*x(1)+3*x(2)-24)^2)^(1/2)',x0,a,b,[],[],lb,ub);
f1=-3*x(1)+2*x(2);
f2=4*x(1)+3*x(2);

 

2.线性加权法：

 

 

 

求解的matlab程序为：

 

f=[-0.5;-2.5];
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
ub=[];
x=linprog(f,a,b,[],[],lb,ub);

 

输出结果为：x1=0.0000,x2=6.0000,对应的目标值为f1=12.0000,f2=18.0000

3.最大最小法

 

 

 

首先编写M函数文件：

 

function f=mutiplesubjiect(x)
f(1)=3*x(1)-2*x(2);
f(2)=-4*x(1)-3*x(2);

 

然后输入

 

>> x0=[0;0];
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
[x,favl]=fminimax('mutiplesubjiect',x0,a,b,[],[],lb,[])

 

4.目标规划法

 

首先编写M函数文件，和上述M函数相同。然后输入：

goal=[12,24];
weight=[12,24];
x0=[0;0];
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
[x,fval]=fgoalattain('mutiplesubjiect',goal,weight,x0,a,b,[],[],lb,[])

输出结果为：x1=0.0000,x2=6.0000,对应的目标值为f1=12.0000,f2=18.0000

5.模糊数学解法

 

 

求解的matlab程序为：

 

f=[0;0;-1];
a=[3 -2 27
   -4 -3 24
   2 3 0
   2 1 0];
b=[15;0;18;10];
lb=[0;0;0];
ub=[];
[x,favl]=linprog(f,a,b,[],[],lb,ub);
f1=-3*x(1)+2*x(2);
f2=4*x(1)+3*x(2);

 

输出结果为：x1=1.0253,x2=5.3165,x3=0.8354,对应的目标值为f1=7.5570,f2=20.0506