深度学习/机器学习入门基础数学知识整理(三):凸优化,Hessian,牛顿法
凸优化理论本身非常博大,事实上我也只是了解了一个皮毛中的皮毛,但是对于广大仅仅想要了解一下机器学习或者深度学习的同学来说,稍微了解一点凸优化也就够了。在实际工程问题中,比如现在我们用的最多的深度神经网络的求解优化问题,都是非凸的,因此很多凸优化理论中非常有价值的定理和方法,在非凸优化问题中不适用,或者说并没有收敛保证等。但是,作为知识的基础,依然有必要来理解和学习一下凸优化,本篇整理了非常基础的一些概念。主要参考网上一些资料,和《凸优化》这本书的一些概念。
凸优化理论基础中的基础
1. 为什么要学习凸优化?
凸优化在数学规划领域具有非常重要的地位。一旦将一个实际问题表述为凸优化问题,大体上意味着相应问题已经得到彻底解决,这是非凸的优化问题所不具有的性质。其应用非常广泛,机器学习中很多优化问题都要通过凸优化来求解;在非凸优化中,凸优化同样起到重要的作用,很多非凸优化问题,可以转化为凸优化问题来解决;
4. 什么是凸函数?

有一个经典的示意图:
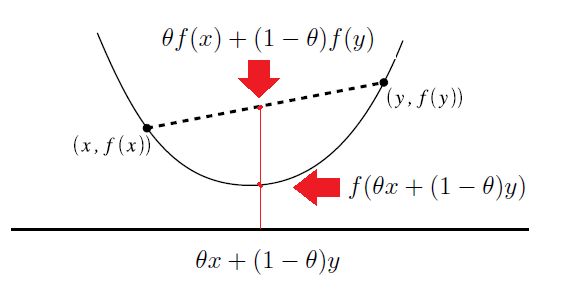
凸函数的几何意义表示为函数任意两点的连线上的取值大于该点在函数上的取值
5. 凸函数的一阶充要条件
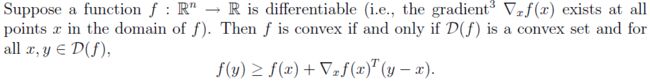
一阶条件的意义是,对于函数在定义域的任意取值,函数的值都大于或者等于对函数在这点的一阶近似。用图来说明就是下图:

口语化理解就是说凸函数总是在其任意一点的切线的上方(或者可以有部分相切的)。通过图可以很清楚地理解这个充要条件,但是,具体在应用中,我们不可能对每一个点都去计算函数的一阶导数,因此后面会说道利用凸函数的二阶特征来进行判断一个函数是否是一个凸函数。下面贴一下证明充分性和必要性的过程,来自《convex optimization》,不是很在意的同学可以跳过,直接看下一节。但是建议手推一下,还是比较简单的:
6. 凸函数的二阶充要条件
记函数的一阶导数和二阶导数为g和H,
g = ∇ f = [ ∂ f ∂ x 1 ∂ f ∂ x 2 ⋮ ∂ f ∂ x n ] H = ∇ 2 f = [ ∂ 2 f ∂ 2 x 1 ∂ 2 f ∂ x 1 x 2 ⋯ ∂ 2 f ∂ x 1 x n ∂ 2 f ∂ 2 x 2 x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ 2 x n x 1 ∂ 2 f ∂ x n x 2 ⋯ ∂ 2 f ∂ x n 2 ] g = \nabla f = \begin{bmatrix} \frac{\partial f }{\partial x_1} \\ \frac{\partial f }{\partial x_2} \\ \vdots\\\frac{\partial f }{\partial x_n} \\ \end{bmatrix} \ \ \ \ \quad H = \nabla^2 f = \begin{bmatrix} \frac{\partial^2 f }{\partial^2 x_1}& \frac{\partial^2 f }{\partial x_1 x_2} & \cdots &\frac{\partial ^2 f }{\partial x_1x_n} \\ \frac{\partial^2 f }{\partial^2 x_2x_1}& \frac{\partial^2 f }{\partial x_2^2} &\cdots &\frac{\partial ^2 f }{\partial x_2x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f }{\partial^2 x_nx_1}& \frac{\partial^2 f }{\partial x_n x_2} &\cdots &\frac{\partial ^2 f }{\partial x_n^2} \\ \end{bmatrix} g=∇f=⎣⎢⎢⎢⎢⎡∂x1∂f∂x2∂f⋮∂xn∂f⎦⎥⎥⎥⎥⎤ H=∇2f=⎣⎢⎢⎢⎢⎢⎡∂2x1∂2f∂2x2x1∂2f⋮∂2xnx1∂2f∂x1x2∂2f∂x22∂2f⋮∂xnx2∂2f⋯⋯⋱⋯∂x1xn∂2f∂x2xn∂2f⋮∂xn2∂2f⎦⎥⎥⎥⎥⎥⎤

其中要求函数 f f f二阶可微,则函数 f f f在定义域上式convex函数的充要条件是:函数的二阶导数(即Hessian矩阵)是半正定的,也就是所有的特征值都是大于等于0的。特殊的,对于一元函数,可以退化为 f ′ ′ ( x ) ≥ 0 f''(x) \geq 0 f′′(x)≥0。
凸函数举例 [10]
举例用二阶充要条件来证明log-sum-exp函数是convex的:

最后一步用到了柯西不等式,很巧妙。
Hessian矩阵与牛顿法
上面提到了函数的二阶导数是Hessian矩阵,Hessian矩阵经常用于牛顿法优化方法中。牛顿法是一种迭代求解方法,有一阶和二阶方法,主要应用在两个方面:1、求方程的根, 2、 最优化方法。
(1)牛顿迭代求解方程的根:
并不是所有的方程都有求根公式, 或者求根公式很复杂, 导致求解困难. 利用牛顿法, 可以迭代求解。原理是利用泰勒公式, 在 x 0 x_0 x0处展开, 且展开到一阶, x = x 0 + δ x = x_0 + \delta x=x0+δ
f ( x ) = f ( x 0 ) + ( x – x 0 ) f ’ ( x 0 ) f(x) = f({x_0}) + (x – {x_0})f’({x_0}) f(x)=f(x0)+(x–x0)f’(x0)
求解方程 f ( x ) = 0 f(x) = 0 f(x)=0,即 f ( x 0 ) + ( x – x 0 ) f ’ ( x 0 ) = 0 f({x_0}) + (x – {x_0})f’({x_0}) = 0 f(x0)+(x–x0)f’(x0)=0,整理后得到
x = x 0 – f ( x 0 ) / f ’ ( x 0 ) x = {x_0} – f({x_0})/f’({x_0}) x=x0–f(x0)/f’(x0)
但是因为我们用的是一阶泰勒展开,只能近似相等,求得的解并不能完全使 f ( x ) = 0 f(x) = 0 f(x)=0成立。记这个金近似解为 x 1 x_1 x1,只能说 f ( x 1 ) f(x_1) f(x1)比 f ( x 0 ) f(x_0) f(x0)更接近 f ( x ) = 0 f(x) = 0 f(x)=0的解,因此我们可以写成一个递推公式:
x k + 1 = x k – f ( x k ) / f ’ ( x k ) (3) {x_{k + 1}} = {x_k} – f({x_k})/f’({x_k}) \tag{3} xk+1=xk–f(xk)/f’(xk)(3)
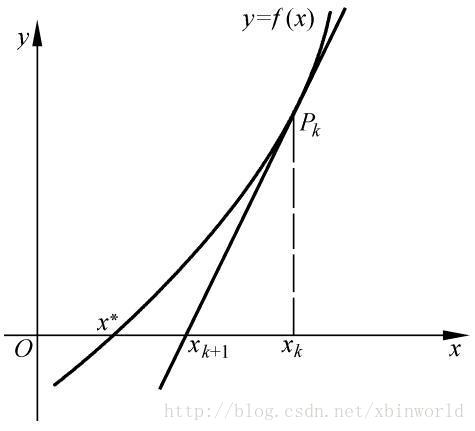
通过迭代, 这个式子必然在 f ( x ∗ ) = 0 f(x^*)=0 f(x∗)=0的时候收敛。 整个过程如下图:
一个比较形象的动态图[9]:从初始点开始每次找f(x)的切线和坐标轴的交点,慢慢逼近真正的f(x)=0点。

(2)二阶优化方法——牛顿法
对于非线性优化问题,牛顿法提供了一种求解的办法。假设任务是优化一个目标函数 f ( x ) f(x) f(x), 求函数 f ( x ) f(x) f(x)的极大或者极小问题, 可以转化为求解函数的导数 f ′ ( x ) = 0 f'(x)=0 f′(x)=0的问题, 这样求可以把优化问题看成方程求解问题。剩下的问题就和第一部分提到的牛顿迭代法求解很相似了。
我们先直接套用一下前面公式(3),但是现在我们要把 f ( x ) f(x) f(x)想象成 f ′ ( x ) f'(x) f′(x),要求 f ′ ( x ) = 0 f'(x)=0 f′(x)=0的根,则:
x n + 1 = x n – f ′ ( x n ) f ′ ′ ( x n ) {x_{n + 1}} = {x_n} – \frac{f'({x_n})}{f''({x_n})} xn+1=xn–f′′(xn)f′(xn)
当然,拓展一下思维,我们也必然可以从泰勒展开获得推导:泰勒展开到二阶:
f ( x + Δ x ) = f ( x ) + f ′ ( x ) Δ x + 1 2 f ′ ′ ( x ) Δ x 2 f(x + \Delta x) = f\left( x \right) + f'(x)\Delta x + \frac{1}{2}f''(x)\Delta {x^2} f(x+Δx)=f(x)+f′(x)Δx+21f′′(x)Δx2挪一下位置得到:
f ( x + Δ x ) − f ( x ) = f ′ ( x ) Δ x + 1 2 f ′ ′ ( x ) Δ x 2 f(x + \Delta x) - f\left( x \right) = f'(x)\Delta x + \frac{1}{2}f''(x)\Delta {x^2} f(x+Δx)−f(x)=f′(x)Δx+21f′′(x)Δx2
假设我们要求 f ( x ) f(x) f(x)的极小值(注:我们并没有假设 f ( x ) f(x) f(x)是convex的,所以可能是一个局部极小值。如果有一定基础的同学,可以把 f ( x ) f(x) f(x)理解为loss function),并且希望一步就要走到尽可能使 f ( x ) f(x) f(x)变小最多(loss尽可能低),那么记,
F = f ′ ( x ) Δ x + 1 2 f ′ ′ ( x ) Δ x 2 ≤ 0 F= f'(x)\Delta x + \frac{1}{2}f''(x)\Delta {x^2} \leq 0 F=f′(x)Δx+21f′′(x)Δx2≤0,并且绝对值最大,所以就是求F最小值。那就容易了,回到了初中数学~~~~对F求导等于0,得到
Δ x = − f ′ ( x ) f ′ ′ ( x ) \Delta x{\rm{ = - }}\frac{{f'({x})}}{{f''({x})}} Δx=−f′′(x)f′(x)
得出牛顿法迭代公式:
x n + 1 = x n − f ′ ( x n ) f ′ ′ ( x n ) , n = 0 , 1 , . . . {x_{n + 1}} = {x_n}{\rm{ - }}\frac{{f'({x_n})}}{{f''({x_n})}},n = 0,1,... xn+1=xn−f′′(xn)f′(xn),n=0,1,...
(这里稍微扯一下一阶方法梯度下降,其实在上一篇中我们已经提到了,这里再强化啰嗦一次,如果只泰勒展开到一阶,那么上面的 f ( x + Δ x ) − f ( x ) = f ′ ( x ) Δ x ≤ 0 f(x + \Delta x) - f\left( x \right)= f'(x)\Delta x \leq 0 f(x+Δx)−f(x)=f′(x)Δx≤0,并且我们要求 f ′ ( x ) Δ x f'(x)\Delta x f′(x)Δx的最小值, Δ x \Delta x Δx的模如果是一个常数,那么它的方向是$ - f('x)$的方向时,取到最小值。所以梯度下降的公式就是: x n + 1 = x n − η ⋅ f ′ ( x ) x_{n + 1} = x_n - \eta \cdot f'(x) xn+1=xn−η⋅f′(x)。其中 η \eta η是步长,表示每次沿着负梯度方向走多远。)
对于高维函数,牛顿法通用公式写成:
x n + 1 = x n − [ H f ( x n ) ] – 1 ∇ f ( x n ) , n ≥ 0 {x_{n + 1}} = {x_n} - {[Hf({x_n})]^{ – 1}}\nabla f({x_n}),n \ge 0 xn+1=xn−[Hf(xn)]–1∇f(xn),n≥0
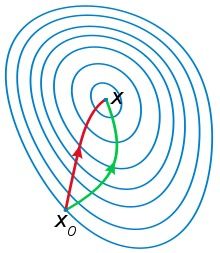
一般认为牛顿法可以利用到曲线本身的信息, 比梯度下降法更容易收敛(迭代更少次数), 如下图是一个最小化一个目标方程的例子, 红色曲线是利用牛顿法迭代求解, 绿色曲线是利用梯度下降法求解:
牛顿法在多变量问题上仍然适用迭代求解,但Hessian矩阵的引入增加了复杂性,特别是当:
▪ Hessian 矩阵非正定,导致目标函数不一定下降,从而牛顿法不收敛;
▪ Hessian 矩阵维度过大带来巨大的计算量。
针对这个问题,在牛顿法无法有效执行的情况下,提出了很多改进方法,比如 拟牛顿法(Quasi-Newton Methods)可以看作是牛顿法的近似。拟牛顿法只需要用到一阶导数,不需要计算Hessian矩阵 以及逆矩阵,因此能够更快收敛,关于拟牛顿法这里不再具体展开,也有更深入的 DFP、BFGS、L-BFGS等算法,大家可以自行搜索学习。总体来讲,拟牛顿法都是用来解决牛顿法本身的复杂计算、难以收敛、局部最小值等问题。
OK,到目前写的几篇深度学习/机器学习入门基础数学知识整理基本涵盖了最最简单的线性代数,矩阵,泰勒展开,凸优化,梯度下降,牛顿法等,如果这些概念你都差不多清楚了,那么就开始学习深度学习或者机器学习吧,可以参考我的机器学习方法系列,以及深度学习方法系列,详见——我的Blog文章索引::机器学习方法系列,深度学习方法系列,三十分钟理解系列等
看了"为什么最速下降法中迭代方向是锯齿形的" [8] [9] [10],补充一下。

最速梯度下降法的算法步骤,如下:

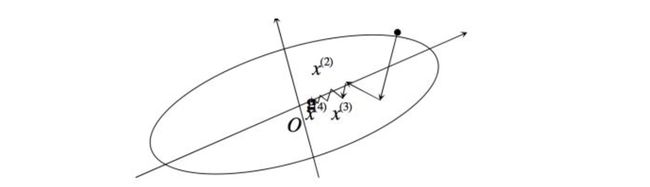
最速梯度下降法中,我们在 x k x^{k} xk 移动到 x k + 1 x^{k+1} xk+1 的过程中,是对移动步长 t k t_{k} tk 进行一维搜索,找到最优的 x k + 1 x^{k+1} xk+1 。下面说明一下
对tk进行一维搜索,要满足
∂ f ( x k − t k ∇ f ( x k ) ) ∂ t k = ∇ f ( x k − t k ∇ f ( x k ) ) ⋅ ( − ∇ f ( x k ) ) = ∇ f ( x k + 1 ) ⋅ ( − ∇ f ( x k ) ) = 0 \frac{\partial f(x^k -t_k \nabla f(x^k))}{\partial t_k} = \nabla f(x^k -t_k \nabla f(x^k))\cdot (-\nabla f(x^k)) = \nabla f(x^{k+1})\cdot (-\nabla f(x^k))=0 ∂tk∂f(xk−tk∇f(xk))=∇f(xk−tk∇f(xk))⋅(−∇f(xk))=∇f(xk+1)⋅(−∇f(xk))=0
可以发现,连续两次梯度方向是垂直的,也就是说最速梯度下降方法中连续两次更新方向是垂直。
参考资料
[1] 《凸优化》(Stephen Boyd等著,王书宁等译)
[2] 凸优化(一)——概述 https://www.jianshu.com/p/fe2e7f0e89e5
[3] 【最优化】通俗理解凸函数及它的一阶特征 http://www.sohu.com/a/216564018_206784
[4] 凸优化简介 http://www.cnblogs.com/ooon/p/5726238.html
[5] 无约束优化方法(梯度法-牛顿法-BFGS- L-BFGS)http://www.cnblogs.com/ooon/p/5729982.html
[6] Jacobian矩阵和Hessian矩阵http://jacoxu.com/jacobian%E7%9F%A9%E9%98%B5%E5%92%8Chessian%E7%9F%A9%E9%98%B5/
[7] 牛顿法与Hessian矩阵
http://blog.csdn.net/linolzhang/article/details/60151623
[8] https://zhuanlan.zhihu.com/p/33428233
[9] https://blog.csdn.net/batuwuhanpei/article/details/51979831
[10] 凸优化(二):凸函数的基本概念
[11] 再谈 梯度下降法/最速下降法/Gradient descent/Steepest Descent
[12] 最优化学习笔记(四)——最速下降法