FCN 简单梳理
FCN 简单梳理
作者:xg123321123
出处:http://blog.csdn.net/xg123321123/article/details/53092154
声明:版权所有,转载请联系作者并注明出处
全卷积网络(Fully Convolutional Network)将CNN应用到了图像语义分割领域。
图像语义分割,就是对一张图片上的所有像素点进行分类。
以往的CNN都是对整张图片进行分类,不能识别图片中特定部分的物体,而全卷积网络是对一张图片中的每个像素进行分类,以此达到对图片特定部分进行分类的效果。
1 卷积化(convolutionalization)
卷积化
以往分类的网络通常会在最后使用全连接层,将原来二维特征图转换成一维的固定长度的特征向量,这就丢失了空间信息,最后输出一个特定长度的向量,表示输入图像属于每一类的概率,以此作为分类的标签。
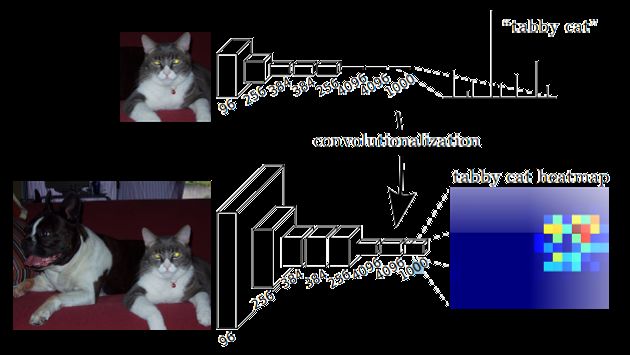
比如将下图输入AlexNet,得到一个长度为1000的输出向量,表示输入图像属于每一类的概率, 其中在“tabby cat”这一类统计概率最高,所以分类标签为“tabby cat”。

与传统CNN在卷积层之后使用全连接层得到固定长度的特征向量进行分类(全连接层+softmax)不同,FCN可以接受任意尺寸的输入图像,然后通过反卷积层对最后一个卷积层的feature map进行上采样, 使它恢复到输入图像相同的尺寸,从而可以对每个像素都产生了一个预测, 同时保留了原始输入图像中的空间信息, 最后在与输入图等大小的特征图上对每个像素进行分类,逐像素地用softmax分类计算损失,相当于每个像素对应一个训练样本。
因为语义分割需要输出整张图片的分割图,所以要求网络中的特征图至少是二维的,这样才能通过上采样还原到输入图片的同等大小。
这就需要替换掉全连接层,改换为卷积层,而这就是卷积化。
上面这幅图展示了卷积化,具体来说,就是将最后仨全连接层替换为卷积层。
全连接层和卷积层的转化
全连接层和卷积层唯一的不同就是卷积层中的神经元只与输入数据中的一个局部区域连接,并且在卷积列中的神经元共享参数。
但是这两类层的神经元都是计算点积,它们的函数形式是一样的。因此,将此两者相互转化是可能的。
对于任意一个卷积层,都存在一个能实现和它一样的前向传播函数的全连接层。权重矩阵是一个巨大的矩阵,除了某些特定块,其余部分都是零。而在其中大部分块中,元素都是相等的。
任何全连接层都可以被转化为卷积层。
假设一个 numout=4096 的全连接层,输入数据体的尺寸是 7∗7∗512,这个全连接层可以被等效地看做一个 Kernel=7,P=0,S=1,numout=4096 的卷积层。
也就是将滤波器的尺寸设置为和输入数据体的尺寸一致了,这个结果就和使用初始的那个全连接层一样了。
全连接层转化为卷积层:在两种变换中,将全连接层转化为卷积层在实际运用中更加有用。
假设卷积神经网络的输入是224x224x3的图像,一系列的卷积层和下采样层将图像数据变为尺寸为 7x7x512 的数据体。AlexNet使用了两个尺寸为4096的全连接层,最后一个有1000个神经元的全连接层用于计算分类评分。
我们可以将这3个全连接层中的任意一个转化为卷积层:
第一个连接区域是[7x7x512]的全连接层,令其滤波器尺寸为Kernel=7,这样输出数据体就为[1x1x4096]了;
第二个全连接层,令其滤波器尺寸为Kernel=1,这样输出数据体为[1x1x4096];
最后一个全连接层也做类似的,令其Kernel=1,最终输出为[1x1x1000]。
转化的意义
这样的变换每次都需要把全连接层的权重 W 重塑成卷积层的滤波器。
如果想让卷积网络在一张更大的输入图片上滑动,得到多个输出,那么卷积层可以在单次前向传播中完成全连接层几次才能完成的操作。
假设想让224×224的滑窗,以32的步长在384×384的图片上滑动,将每个位置的特征都提取到网络中,最后得到6×6个位置的类别得分。
如果224×224的输入图片经过卷积层和下采样层之后得到了[7x7x512]的特征图,那么,384×384的大图片直接经过同样的卷积层和下采样层之后会得到[12x12x512]的特征。然后再经过上面由3个全连接层转化得到的3个卷积层,最终得到[6x6x1000]的输出((12 – 7)/1 + 1 = 6)。这个结果正是滑窗在原图中6×6个位置的得分。
对于384×384的图像,让(含全连接层)的初始卷积神经网络以32像素的步长独立对图像中的224×224块进行多次评价,其效果和使用把全连接层变换为卷积层后的卷积神经网络进行一次前向传播是一样的。
所以将全连接层转换成卷积层会更简便。
全卷积网络称谓的由来
FCN将传统CNN中的全连接层转化成卷积层,对应CNN网络FCN把最后三层全连接层转换成为三层卷积层。
在传统的CNN结构中,前5层是卷积层,第6层和第7层分别是一个长度为4096的一维向量,第8层是长度为1000的一维向量,分别对应1000个不同类别的概率。
FCN将这3层转换为卷积层,卷积核的大小 (通道数,宽,高) 分别为 (4096,1,1)、(4096,1,1)、(1000,1,1)。看上去数字上并没有什么差别,但是卷积跟全连接是不一样的概念和计算过程,使用的是之前CNN已经训练好的权值和偏置,但是不一样的在于权值和偏置是有自己的范围,属于自己的一个卷积核。因此FCN网络中所有的层都是卷积层,故称为全卷积网络。
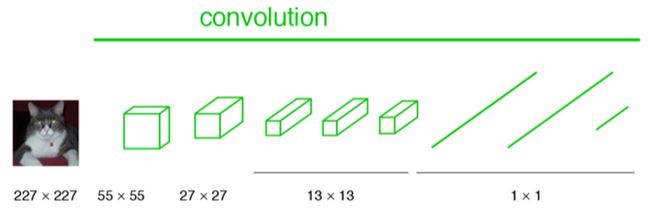
下图是一个全卷积层,与上图不一样的是图像对应的大小下标,CNN中输入的图像大小是同意固定resize成 227x227 大小的图像,第一层pooling后为55x55,第二层pooling后图像大小为27x27,第五层pooling后的图像大小为13*13。
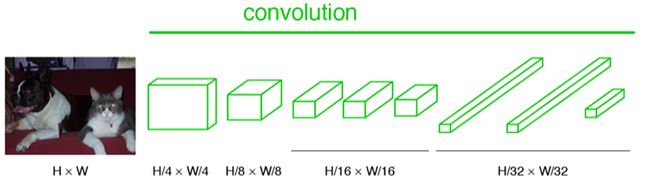
而FCN输入的图像是H*W大小,第一层pooling后变为原图大小的1/4,第二层变为原图大小的1/8,第五层变为原图大小的1/16,第八层变为原图大小的1/32。
经过多次卷积和pooling以后,得到的图像越来越小,分辨率越来越低。其中图像到 H/32∗W/32 的时候图片是最小的一层时,所产生图叫做heatmap热图,热图就是我们最重要的高维特征图,得到高维特征的heatmap之后就是最重要的一步也是最后的一步对原图像进行upsampling,把图像进行放大、放大、放大到原图像的大小。
最后的输出是1000张(因为有1000类)heatmap经过上采样得来的图片。
接着就是对每个像素进行分类预测:逐像素地求其在1000张图像该像素位置的最大数值描述(概率),并将其作为该像素的分类。
这样就产生了一张已经分类好的图片,如下图。

2 反卷积(Deconvolution)
可能叫做转置卷积(Transposed Convolution)更为合适。
反卷积过程可以理解为上采样过程(Upsampling)。
以往的CNN结构,如AlexNet,VGGNet,池化层缩小了特征图的尺寸。
在语义分割中,我们需要输出和输入图像尺寸相同的分割图片,因此需要对特征图进行上采样。
反卷积是卷积的逆过程,先看一下Caffe中的卷积操作,分为两个步骤:
使用im2col操作将图片转换为矩阵
调用GEMM计算实际的结果
举例说明:
4x4的输入,卷积Kernel为3x3, Padding为0,Stride为1, 输出为2x2。
输入矩阵可展开为16维向量,记作 x ;
输出矩阵可展开为4维向量,记作 y ;
卷积运算可表示为 y=Cx ;
神经网络的正向传播就是转换成了如上矩阵进行运算。
接着是反向传播。
首先有了从更深层的网络中得到的 ∂Loss∂y
根据矩阵微分公式
这就是反向传播时的矩阵运算。
而反卷积运算和卷积运算在神经网络的正向和反向传播刚好相反。
所以反卷积其实就是正向时左乘 CT ,而反向时左乘 (CT)T ,即 C 的运算。
注意:
为了得到和输入图像尺寸完全相同的特征图,FCN中还使用了crop操作来辅助反卷积操作,因为反卷积操作并不是将特征图恰好放大整数倍。
3 跳跃结构(Skip Architecture)
经过前两步操作,基本就能实现语义分割了,但是直接将全卷积后的结果进行反卷积,得到的结果往往比较粗糙。
如上图所示,对原图像进行卷积conv1、pool1后原图像缩小为1/2;之后对图像进行第二次conv2、pool2后图像缩小为1/4;接着继续对图像进行第三次卷积操作conv3、pool3缩小为原图像的1/8,此时保留pool3的featureMap;接着继续对图像进行第四次卷积操作conv4、pool4,缩小为原图像的1/16,保留pool4的featureMap;最后对图像进行第五次卷积操作conv5、pool5,缩小为原图像的1/32,然后把原来CNN操作中的全连接变成卷积操作conv6、conv7,图像的featureMap数量改变但是图像大小依然为原图的1/32,此时图像不再叫featureMap而是叫heatMap。
现在我们有1/32尺寸的heatMap,1/16尺寸的featureMap和1/8尺寸的featureMap,1/32尺寸的heatMap进行upsampling操作之后,因为这样的操作还原的图片仅仅是conv5中的卷积核中的特征,限于精度问题不能够很好地还原图像当中的特征,因此在这里向前迭代。把conv4中的卷积核对上一次upsampling之后的图进行反卷积补充细节(相当于一个插值过程),最后把conv3中的卷积核对刚才upsampling之后的图像进行再次反卷积补充细节,最后就完成了整个图像的还原。
具体来说,就是将不同池化层的结果进行上采样,然后结合这些结果来优化输出,具体结构如下:
本篇博客主要参考自
《FCN学习:Semantic Segmentation》
《如何理解深度学习中的deconvolution networks?》
《全卷积网络 FCN 详解》