leetcode二叉树面试题目集锦
优势
在实际使用时会根据链表和有序数组等数据结构的不同优势进行选择。有序数组的优势在于二分查找,链表的优势在于数据项的插入和数据项的删除。但是在有序数组中插入数据就会很慢,同样在链表中查找数据项效率就很低。综合以上情况,二叉树可以利用链表和有序数组的优势,同时可以合并有序数组和链表的优势,二叉树也是一种常用的数据结构。
定义
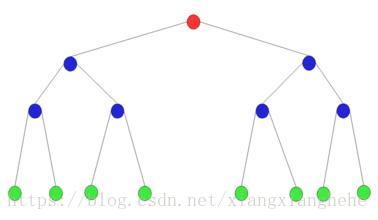
二叉树由节点(node)和边组成。节点分为根节点、父节点、子节点。如下图所示
红色是根节点root。蓝色是子节点也是父节点,绿色的是子节点。其余的线是边。节点和链表中的节点一样都可以存放数据信息。树中的边可以用自引用表示,这种引用就是C/C++里面的指针。通常来说树是顶部小,底部大,且树呈分层结构。root节点时第0层,以此类推。另外, 二叉树最多有两个节点。
###结构体定义
struct BinaryTreeNode {
int value;
BinaryTreeNode* left;
BinaryTreeNode* right;
BinaryTreeNode(int x) : value(x), left(NULL), right(NULL) {}
};
初始化
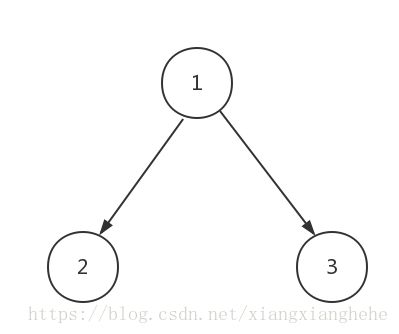
我们直接简单初始化:根节点为1,左节点为2,右节点为3,如图所示:
对应code如下:
void init(BinaryTreeNode *root)
{
root ->value = 1;
BinaryTreeNode *left = new BinaryTreeNode(2);
BinaryTreeNode *right = new BinaryTreeNode(3);
root->left = left;
root->right = right;
}
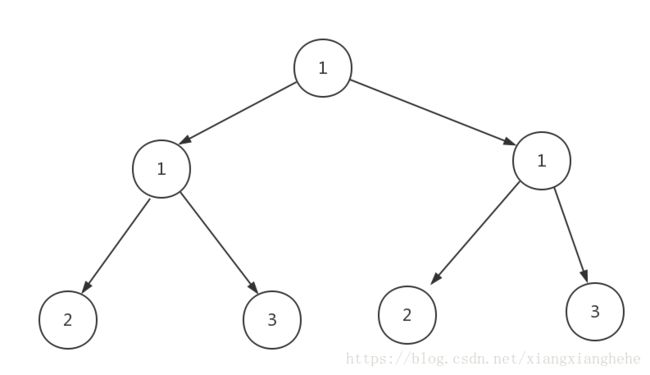
可以直接把一个一个初始化好的二叉树接到节点上,例如:
对应code如下:
void init(BinaryTreeNode *root)
{
root ->value = 1;
BinaryTreeNode *head = new BinaryTreeNode(1);
BinaryTreeNode *left = new BinaryTreeNode(2);
BinaryTreeNode *right = new BinaryTreeNode(3);
head -> left = left;
head -> right = right;
root -> left = head;
root -> right = head;
}
求二叉树节点个数
/*
如果二叉树为空,节点个数为0
如果二叉树不为空,二叉树节点个数 = 左子树节点个数 + 右子树节点个数 + 1
*/
int getNodenum(BinaryTreeNode *head)
{
if(head == nullptr) return 0;
else
{
return getNodenum(head->left) + getNodenum(head->right) +1;
}
}
求二叉树的深度
/*
如果二叉树为空,二叉树的深度为0
如果二叉树不为空,二叉树的深度 = max(左子树深度, 右子树深度) + 1
*/
int getDegree(BinaryTreeNode *head)
{
if(head == nullptr) return 0;
else
{
int max_degree = getDegree(head->left)>getDegree(head->right)?getDegree(head->left):getDegree(head->right);
return max_degree + 1;
}
}
前序遍历,中序遍历,后序遍历
三种遍历其实用递归很容易,不过还是建议也顺便掌握下非递归遍历方法.
前序遍历递归解法:如果二叉树为空,空操作;如果二叉树不为空,访问根节点,前序遍历左子树,前序遍历右子树。
中序遍历递归解法:如果二叉树为空,空操作;如果二叉树不为空,中序遍历左子树,访问根节点,中序遍历右子树。
后序遍历递归解法:如果二叉树为空,空操作;如果二叉树不为空,后序遍历左子树,后序遍历右子树,访问根节点。
代码如下:
void preOrderTraverse(BinaryTreeNode* head)
{
if(head == nullptr) return ;
else
{
cout << head->value < left);
preOrderTraverse(head -> right);
}
}
void inOrderTraverse(BinaryTreeNode* head)
{
if(head == nullptr) return ;
else
{
inOrderTraverse(head -> left);
cout << head->value < right);
}
}
void postOrderTraverse(BinaryTreeNode* head)
{
if(head == nullptr) return ;
else
{
postOrderTraverse(head -> left);
postOrderTraverse(head -> right);
cout << head->value < 层次遍历
二叉树层次遍历相当于广度优先搜索,使用队列实现。队列初始化,将根节点压入队列。当队列不为空,进行如下操作:弹出一个节点,访问,若左子节点或右子节点不为空,将其压入队列。
void LevelTraverse(BinaryTreeNode* root)
{
if(root == NULL) return ;
queue que;
que.push(root);
while(!que.empty())
{
BinaryTreeNode* tempNode = que.front();
que.pop();
visit(tempNode); //cout <value <left != NULL) que.push(tempNode->left);
if(root->right != NULL) que.push(tempNode->right);
}
return ;
}
求二叉树第K层的节点个数
这个可以用递归思路很快求解:
如果二叉树为空或者k<1返回0
如果二叉树不为空并且k==1,返回1
如果二叉树不为空且k>1,返回左子树中k-1层的节点个数与右子树k-1层节点个数之和
代码如下:
int getKthnum(BinaryTreeNode* head, int k)
{
if(head == nullptr || k < 1) return 0;
if (k==1) return 1;
int left_num = getKthnum(head->left);
int right_num = getKthnum(head->right);
return left_num + right_num;
}
求二叉树中叶子节点的个数
这个可以用递归思路也可以很快求解:
如果二叉树为空,返回0;
如果二叉树不为空且左右子树为空,返回1;
如果二叉树不为空,且左右子树不同时为空,返回左子树中叶子节点个数加上右子树中叶子节点个数。
int GetLeafNodeNum(BinaryTreeNode * head)
{
if(head == nullptr) return 0;
if (head->left == nullptr && head->right ==nullptr) return 1;
int left_num = GetLeafNodeNum(head->left);
int right_num = GetLeafNodeNum(head->right);
return left_num + right_num;
}
判断两棵二叉树是否结构相同
不考虑数据内容。结构相同意味着对应的左子树和对应的右子树都结构相同。这个可以用递归思路也可以很快求解:
如果两棵二叉树都为空,返回真
如果两棵二叉树一棵为空,另一棵不为空,返回假
如果两棵二叉树都不为空,如果对应的左子树和右子树都同构返回真,其他返回假
bool isBinarytreeEqual(BinaryTreeNode * tree1, BinaryTreeNode * tree2)
{
if(tree1 == nullptr && tree2 == nullptr) return true;
else if(tree1 == nullptr || tree2 == nullptr) return false;
else
{
bool isLeftEqual = isBinarytreeEqual(tree1->left, tree2->left);
bool isRightEqual = isBinarytreeEqual(tree1->right, tree2->right);
return (tree1->value == tree2->value )&&isLeftEqual && isRightEqual;
}
}
判断一棵树是否是平衡二叉树
根据二叉树的定义,我们可以递归遍历二叉树的每一个节点来,求出每个节点的左右子树的高度,如果每个节点的左右子树的高度相差不超过1,按照定义,它就是一颗平衡二叉树。
class Solution {
public:
bool isBalanced(TreeNode* root) {
if(root == nullptr)
return true;
int left = depth(root->left);
int right = depth(root->right);
bool flag = abs(left - right) <=1?true:false;
return flag && isBalanced(root->left) && isBalanced(root->right);
}
int depth(TreeNode* root)
{
if(root == nullptr)
return 0;
int left_depth = depth(root->left);
int right_depth = depth(root->right);
return max(left_depth, right_depth) + 1;
}
};
二叉树翻转(二叉树镜像)
这里是要求把二叉树进行左右子树翻转
递归实现:
#include
using namespace std;
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
class Solution {
public:
void Mirror(TreeNode *pRoot) {
if(pRoot==NULL)
{
return;
}
swap(pRoot->left,pRoot->right);
Mirror(pRoot->right);
Mirror(pRoot->left);
}
};
或者
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr)
return nullptr;
invertTree(root->right);
invertTree(root->left);
swap(root->left,root->right);
/*
TreeNode* tmp = root->left;
root->left = root->right;
root->right = tmp;
*/
return root;
}
};
非递归实现:
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
void Mirror(TreeNode *pRoot) {
if(pRoot==NULL)
{
return;
}
queue q;
q.push(pRoot);
while(!q.empty())
{
TreeNode *per = q.front();
TreeNode *tmp = per->left;
per->left = per->right;
per->right = tmp;
if(per->right!=NULL)
{
q.push(per->right);
}
if(per->left!=NULL)
{
q.push(per->left);
}
}
q.pop();
}
}
二叉树的右视图(二叉树最右边节点)
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:
1 <---
/ \
2 3 <---
\ \
5 4 <---
其实就是考察二叉树的层次遍历,用队列实现:
class Solution {
public:
vector rightSideView(TreeNode* root) {
vector ivec;
if(root != nullptr)
{
queue Queue;
Queue.push(root);
while(!Queue.empty())
{
ivec.push_back(Queue.front()->val);
int size = Queue.size();
for(int i = 1;i <= size;++i)
{
TreeNode *Node = Queue.front();
Queue.pop();
if(Node->right != NULL)
Queue.push(Node->right);
if(Node->left != NULL)
Queue.push(Node->left);
}
}
}
return ivec;
}
};
代码合并起来
#include
using namespace std;
struct BinaryTreeNode {
int value;
BinaryTreeNode* left;
BinaryTreeNode* right;
BinaryTreeNode(int x) : value(x), left(nullptr), right(nullptr) {}
};
/*
如果二叉树为空,节点个数为0
如果二叉树不为空,二叉树节点个数 = 左子树节点个数 + 右子树节点个数 + 1
*/
int getNodenum(BinaryTreeNode *head)
{
if(head == nullptr) return 0;
else
{
return getNodenum(head->left) + getNodenum(head->right) +1;
}
}
/*
如果二叉树为空,二叉树的深度为0
如果二叉树不为空,二叉树的深度 = max(左子树深度, 右子树深度) + 1
*/
int getDegree(BinaryTreeNode *head)
{
if(head == nullptr) return 0;
else
{
int max_degree = getDegree(head->left)>getDegree(head->right)?getDegree(head->left):getDegree(head->right);
return max_degree + 1;
}
}
void init(BinaryTreeNode *root)
{
root ->value = 1;
BinaryTreeNode *head = new BinaryTreeNode(1);
BinaryTreeNode *left = new BinaryTreeNode(2);
BinaryTreeNode *right = new BinaryTreeNode(3);
head -> left = left;
head -> right = right;
root -> left = head;
root -> right = head;
}
void preOrderTraverse(BinaryTreeNode* head)
{
if(head == nullptr) return ;
else
{
cout << head->value < left);
preOrderTraverse(head -> right);
}
}
void inOrderTraverse(BinaryTreeNode* head)
{
if(head == nullptr) return ;
else
{
inOrderTraverse(head -> left);
cout << head->value < right);
}
}
void postOrderTraverse(BinaryTreeNode* head)
{
if(head == nullptr) return ;
else
{
postOrderTraverse(head -> left);
postOrderTraverse(head -> right);
cout << head->value <left, k-1);
int right_num = getKthnum(head->right, k-1);
return left_num + right_num;
}
int GetLeafNodeNum(BinaryTreeNode * head)
{
if(head == nullptr) return 0;
if (head->left == nullptr && head->right ==nullptr) return 1;
int left_num = GetLeafNodeNum(head->left);
int right_num = GetLeafNodeNum(head->right);
return left_num + right_num;
}
int treeDepth(BinaryTreeNode * root)
{
if(root == nullptr) return 0;
int nLeft=treeDepth(root->left);
int nright=treeDepth(root->right);
return nLeft>nright?nLeft+1:nright+1;
}
bool isAVL(BinaryTreeNode * root)
{
if(root == nullptr) return true;
int left= treeDepth(root->left);
int right= treeDepth(root->right);
return abs(left - right) <=1?true:false;
}
int main()
{
BinaryTreeNode *root;
init(root);
int degree = getDegree(root);
cout <<"degree is: "<