《大话数据结构》笔记
一、数据结构绪论
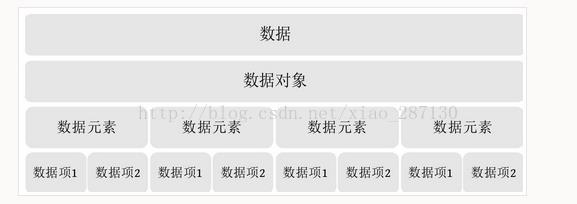
1、数据:是描述客观事物的符号,是计算机中可以操作的对象,是能被计算机识别,并输入给计算机处理的符号集合。
2、数据元素:是组成数据的、有一定意义的基本单位,在计算机中通常作为整体处理。也被称为记录。
3、数据项:一个数据元素可以由若干个数据项组成。
4、数据项是数据不可分割的最小单位。
5、不同数据元素之间不是独立的,而是存在特定的关系,我们将这些关系称为结构。
数据结构:是相互之间存在一种或多种特定关系的数据元素的集合。
6、逻辑结构
6.1 集合结构:
集合结构中的数据元素除了同属于一个集合外,它们之间没有其他关系。
6.2 线性结构:
线性结构中的数据元素之间是一对一的关系
6.3 树形结构:
树形结构中的数据元素之间存在一种一对多的层次关系
6.4 图形结构:
图形结构的数据元素是多对多的关系
7、物理结构
是指数据的逻辑结构在计算机中的存储形式
7.1 顺序存储结构:
是把数据元素存放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的
7.2 链式存储结构:
是把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的。
二、算法
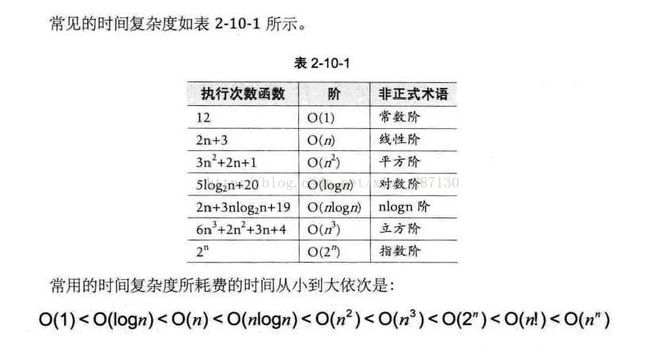
1、时间复杂度
用我们推导大O阶的方法:(eg: n^2/2 + n/2 )
(1)加法常数不考虑;(2)只保留最高阶,所以n^2/2;(3)去除这个项相乘的常数,去除1/2;
最终时间复杂度为O(n^2);
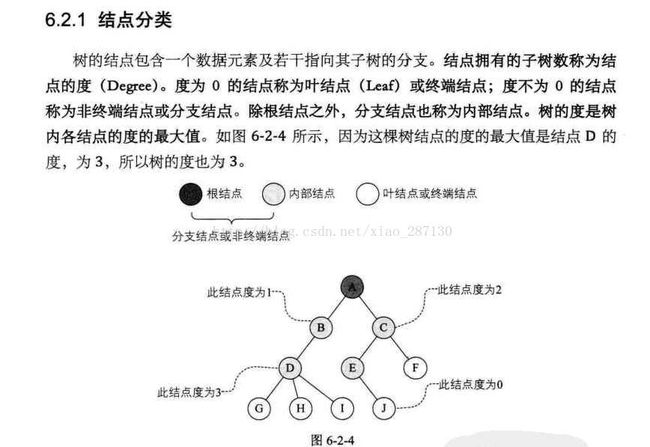
六、树
1、树是n(n>=0)个结点的有限集合。
n=0是称为空树。
在任何一棵非空树中:
(1)有且只有一个特定的称为根的结点;
(2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集合T1、T2.......Tm,其中每一个集合本身又是一棵树,并且称为跟的子树。
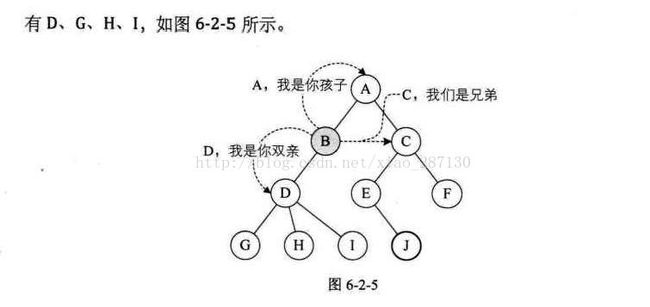
2、树的存储结构
(1)、双亲表示法
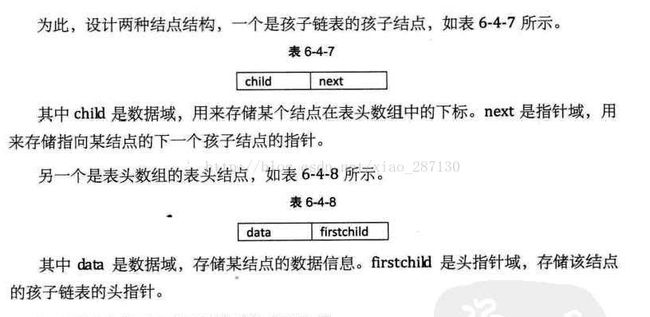
(2)孩子表示法
把每个结点的孩子结点排列起来,已单链表作存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空。
然后n个头指针又组成一个线性表,采用顺序结构,存放进一个一维数组中。
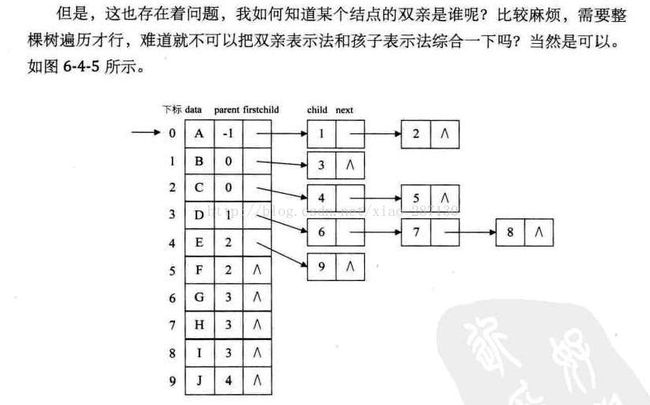
****双亲孩子表示法
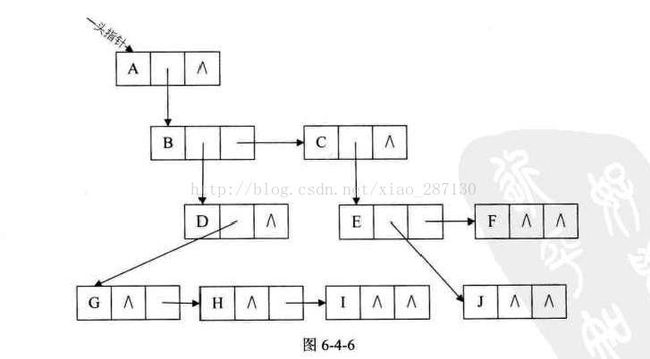
(3)孩子兄弟表示法
3、二叉树
是n(n>=0)个结点的有限集合,改集合或者为空(空二叉树),或者有一个根节点和两颗互不相交、分别称为跟结点的左子树和右子树的二叉树组成。
3.1 特殊二叉树
(1)斜数
(2)满二叉树
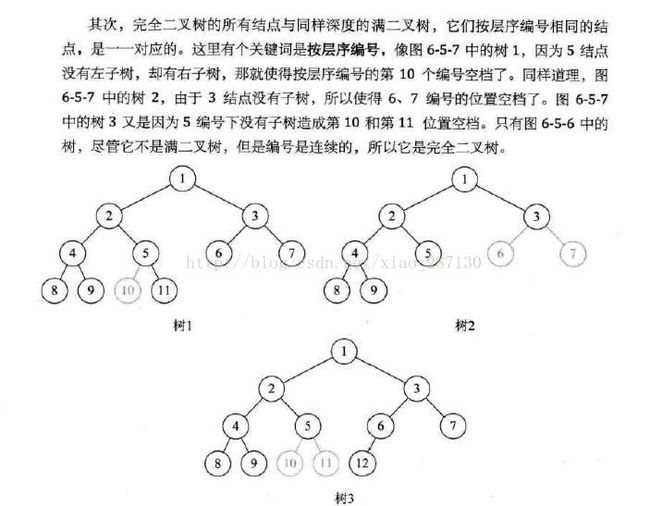
(3)完全二叉树
![]()
3.2 二叉树性质
(1) 在二叉树第i层上至多有 2^(i-1) 个结点。(i>=1)
(2)深度为k的二叉树至多有 2^k - 1 个结点.(k>=1)
(3) 对任何二叉树T,其终端结点数为n0,度为2的结点数为n2,则 n0 = n2 + 1.
(4)性质4
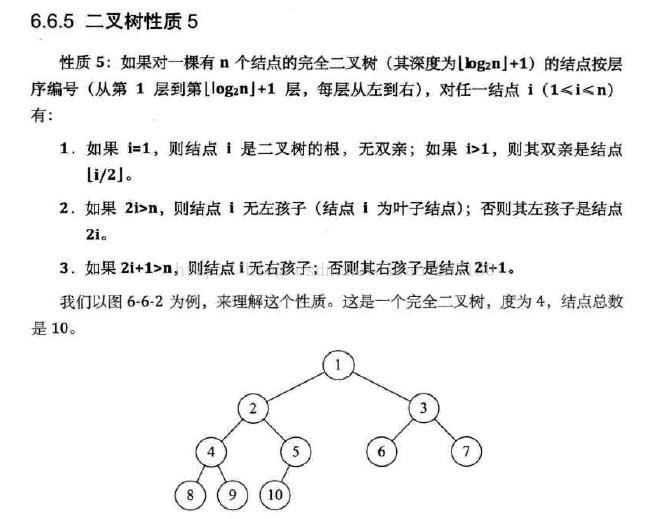
(5)性质5
3.3 二叉树的存储结构
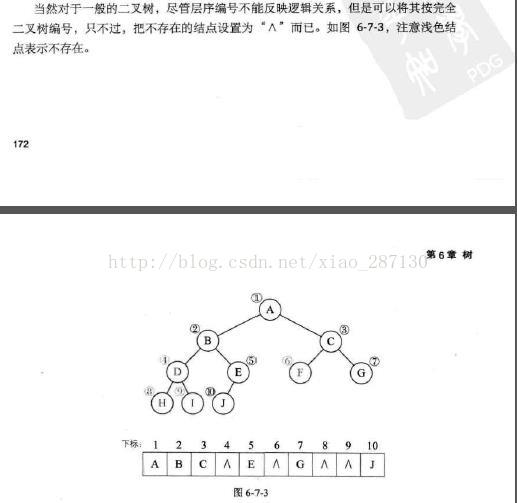
(1)顺序储存结构
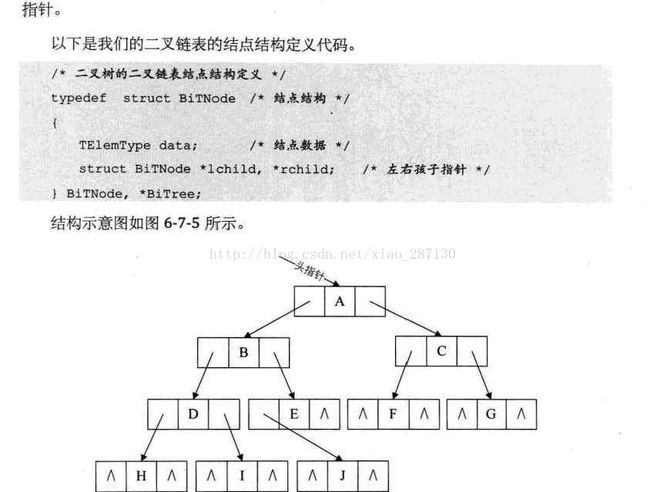
(2)二叉链表结构
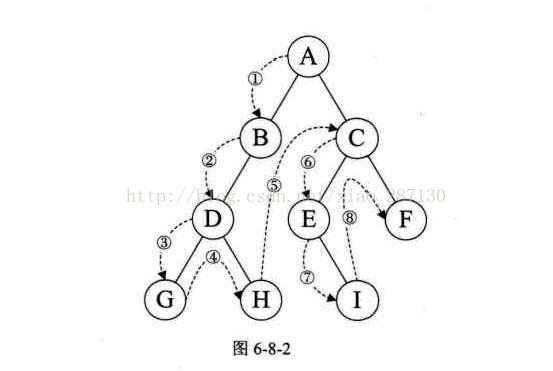
3.4 遍历二叉树
(1)前序遍历
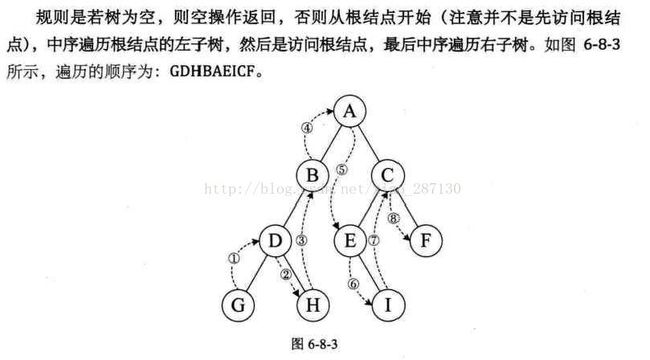
(2)中序遍历
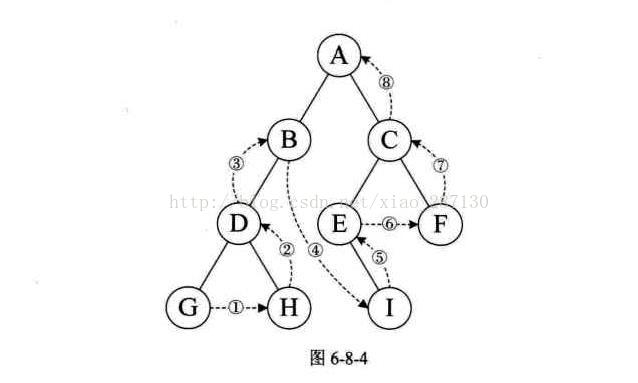
(3)后序遍历
3.5 二叉树遍历性质
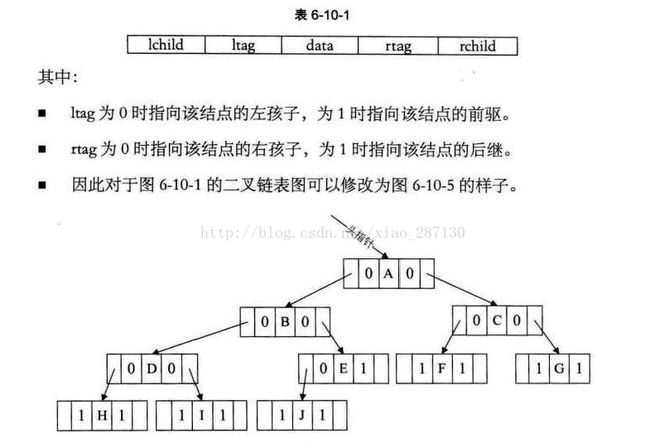
3.6 线索二叉树
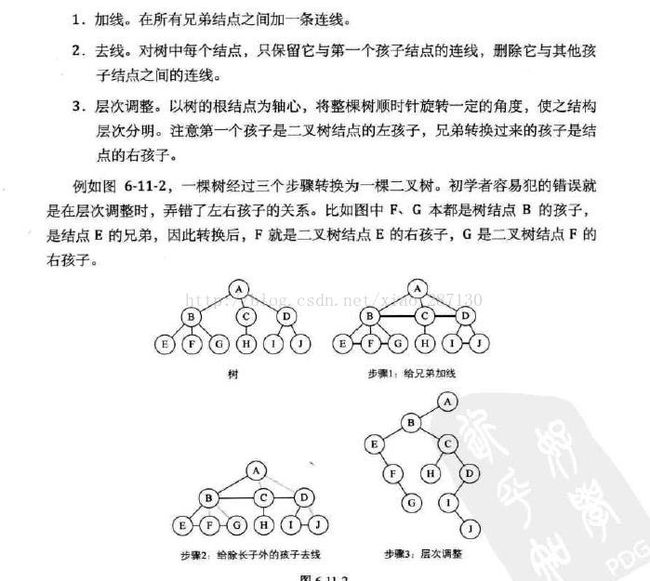
3.7 树转换为二叉树
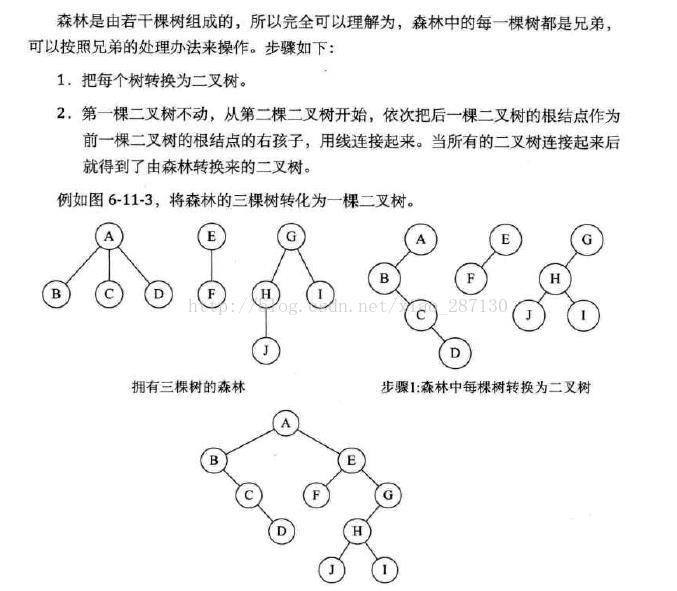
3.8 森林转换为二叉树
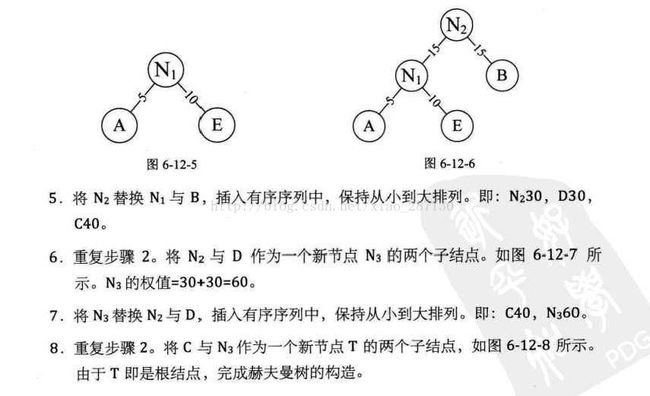
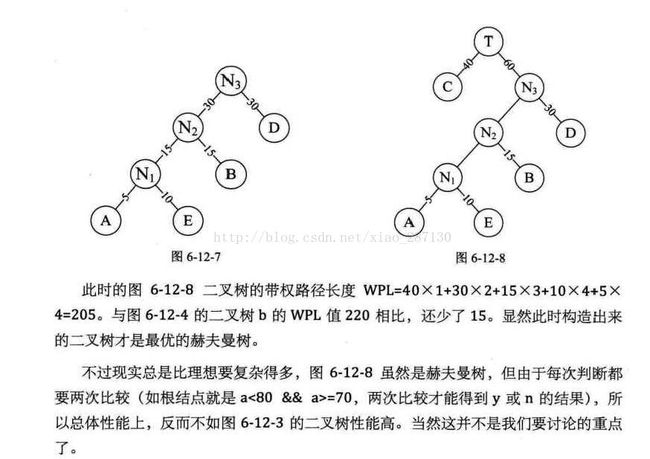
3.9 赫夫曼树
从树中一个结点到另一个结点之间的分支构成两个结点之间的路径,路径上的分支数目称做路径长度。
树的路径长度就是从树根到到每一个结点的路径长度之和。
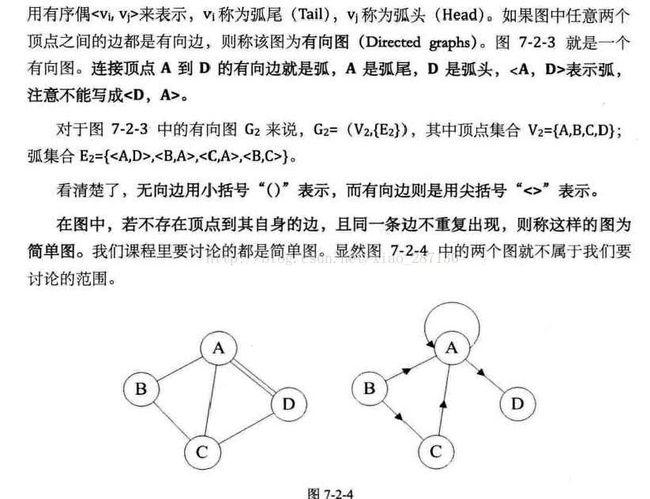
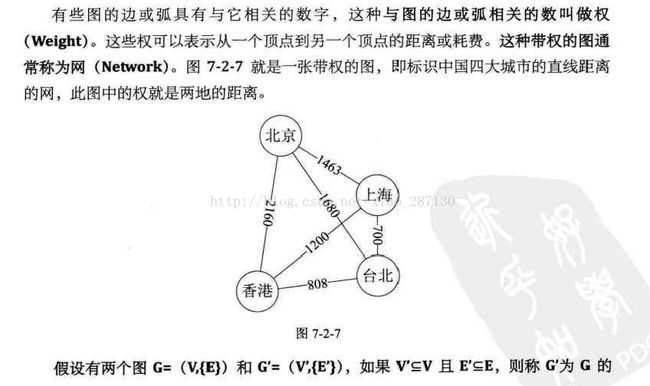
四、图
4.2 图的顶点与边的关系
4.3 图的储存结构
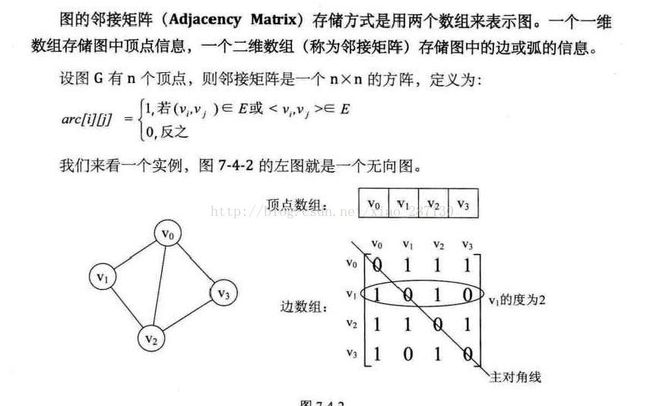
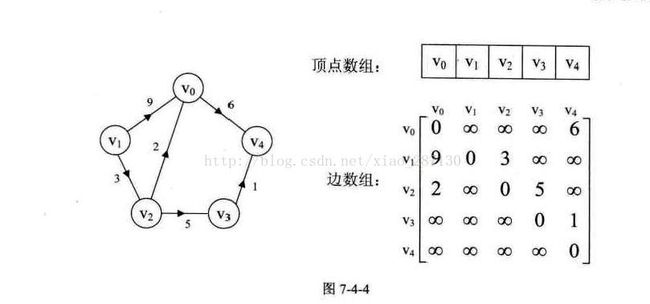
(1) 邻接矩阵
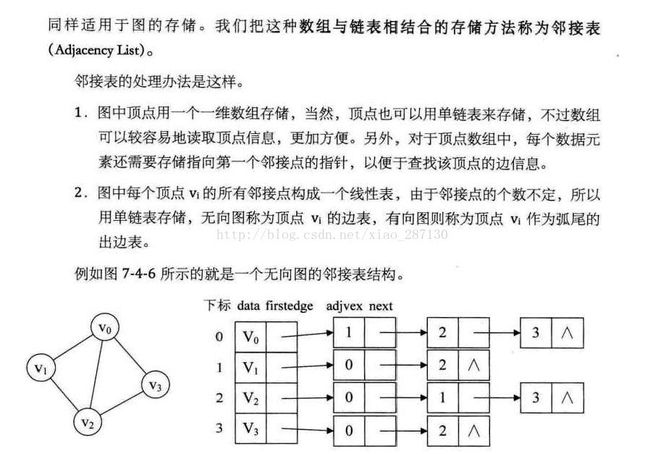
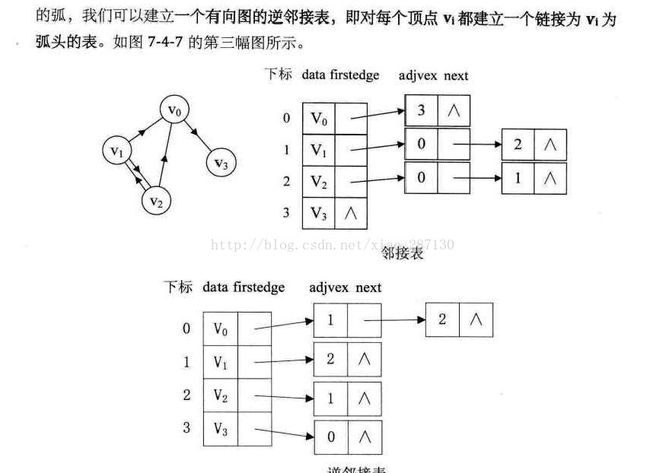
(2)邻接表
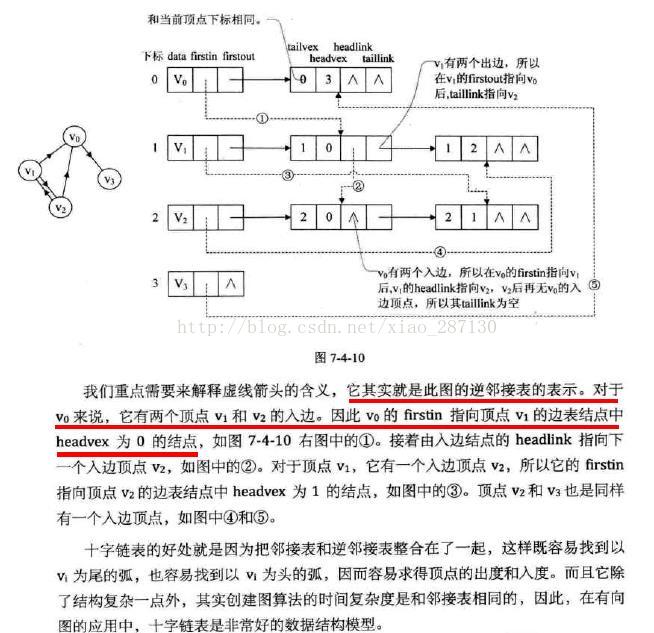
(3) 十字链表
八、查找
1、有序表查找
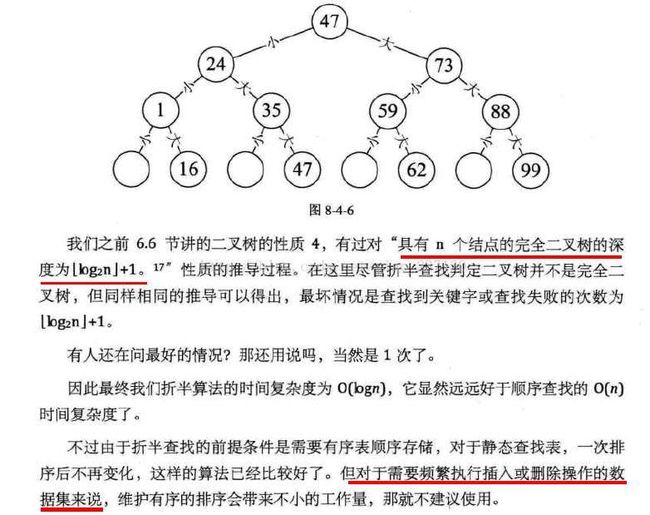
1)折半查找
2) 插值查找
3)斐波那契查找
2、线性索引查找
3、二叉排序树
2) 插入操作
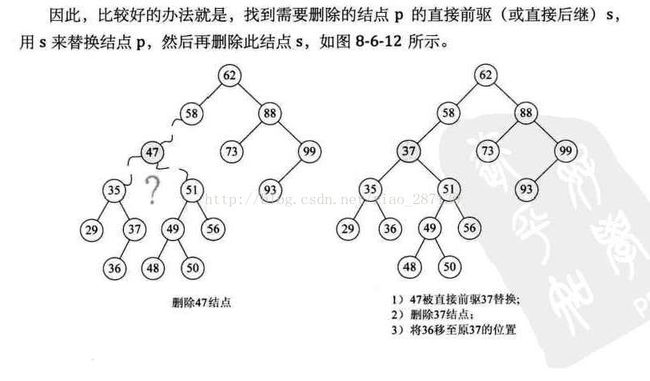
3) 删除操作
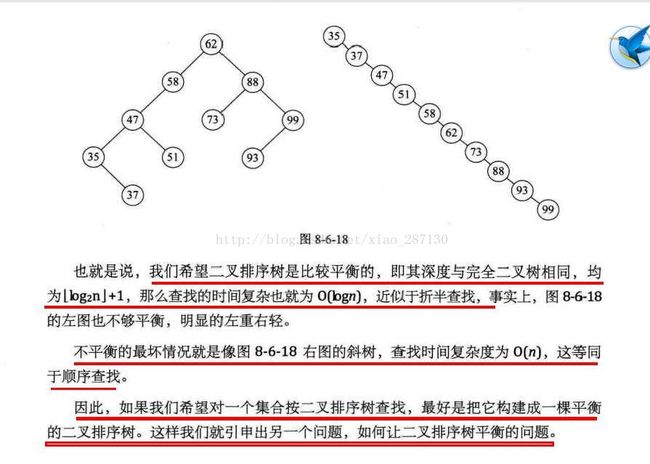
4、平衡二叉树 AVL
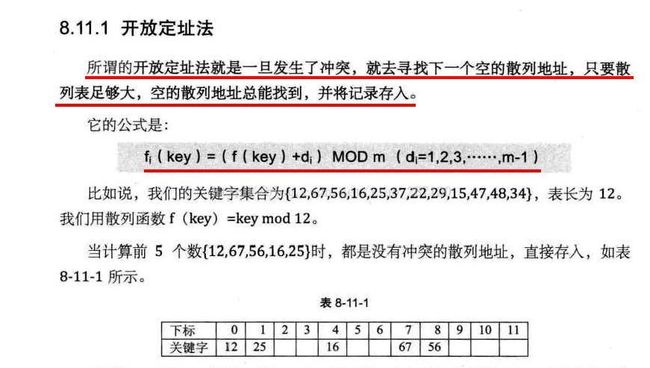
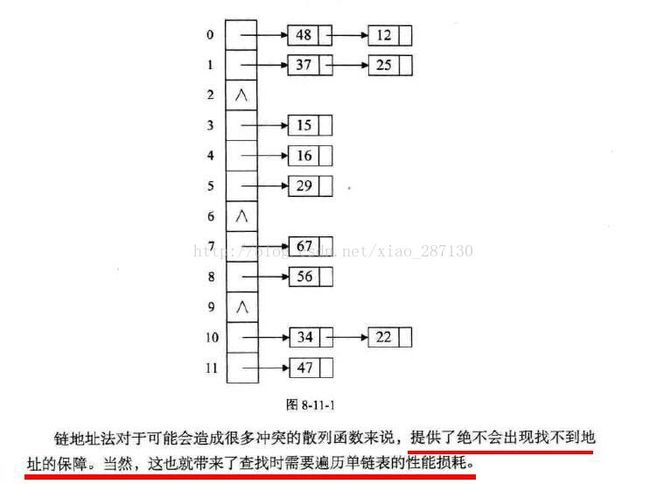
4、散列表查找(哈希)
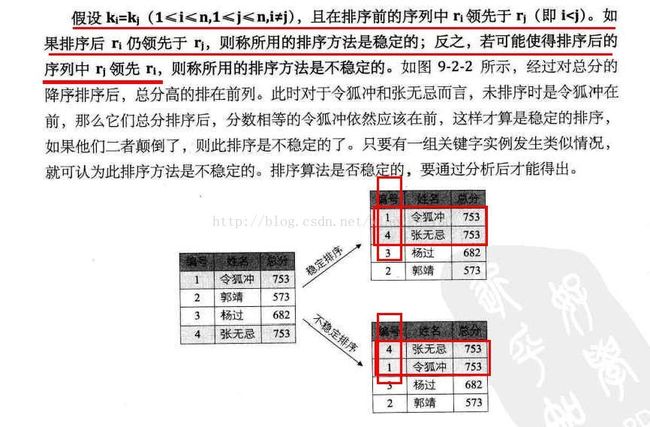
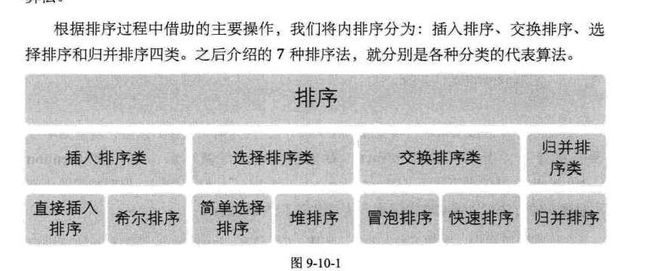
九、排序
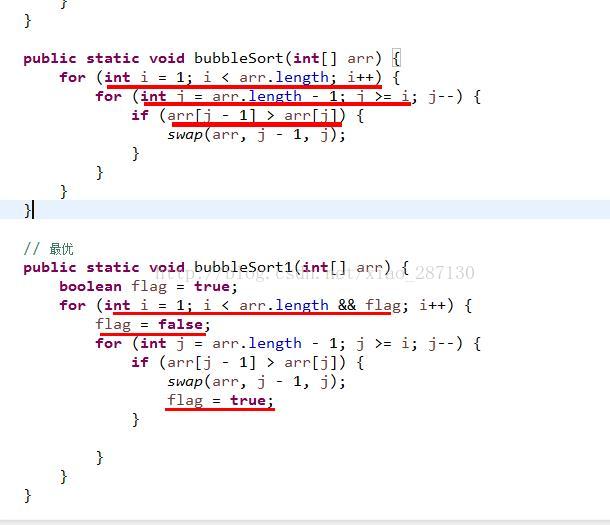
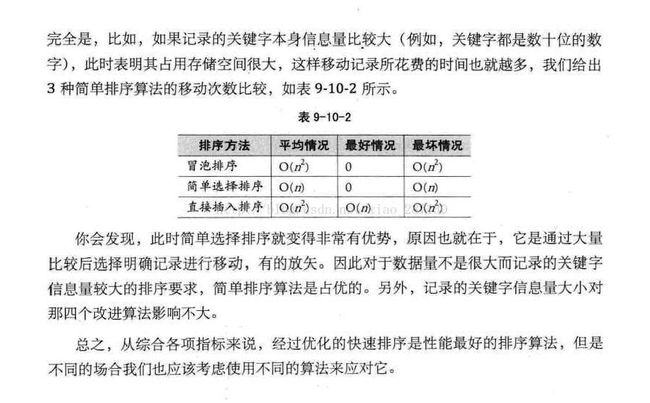
1、冒泡排序
2、简单选择排序
3、直接插入排序
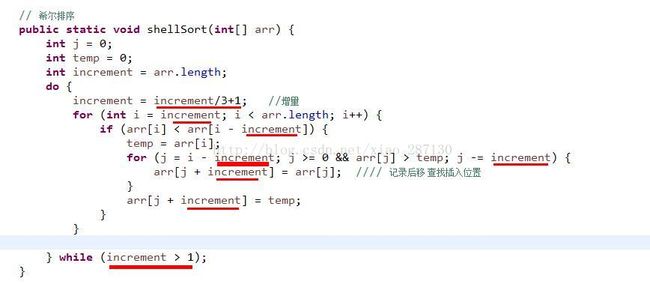
4、希尔排序
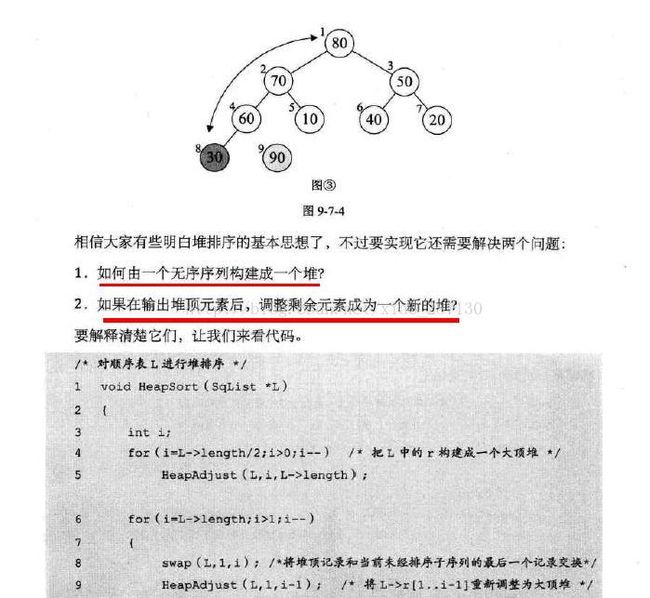
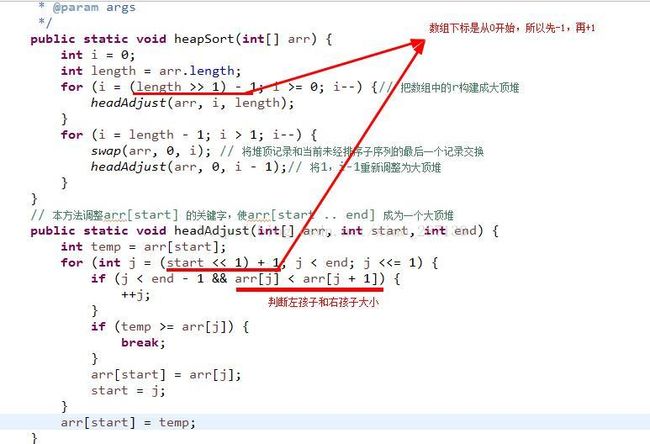
5、堆排序
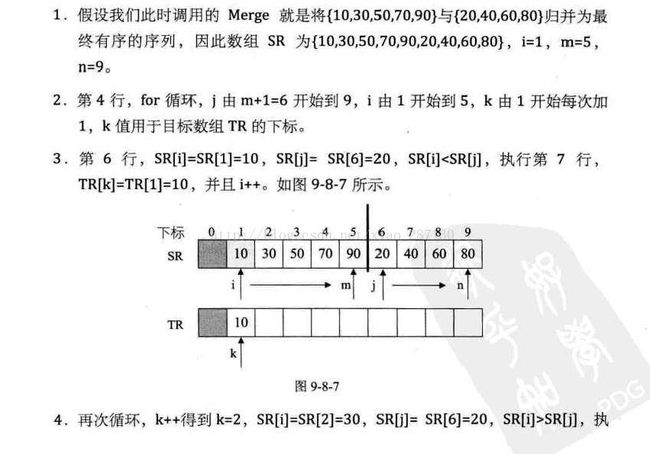
6、归并排序
6.1 递归排序
算法:
/**
* 归并排序
*
* @param args
*/
public static void mergeSort(int[] arr) {
mSort(arr, 0, arr.length - 1);
}
// 将arr[start..end] 归并排序为arrTR2[start..end]
public static void mSort(int[] arr, int left, int right) {
if (left < right) {
int center = (left + right) / 2; // 将arr[start..end]平分为arr[start..m]和arr[m+1..end]
mSort(arr, left, center);
mSort(arr, center + 1, right);
merge(arr, left, center, right);
}
}
public static void merge(int[] arr, int left, int center, int right) {
int mid = center+1;// 右指针
int third = left;// 左指针
int tmp = left;
int[] temp = new int[arr.length+1];
while (left <= center && mid <= right) {// 把较小的数先移到新数组中
if (arr[left] < arr[mid]) {
temp[third++] = arr[left++];
} else {
temp[third++] = arr[mid++];
}
}
while(mid <= right){// 把右边边剩余的数移入数组
temp[third++] = arr[mid++];
}
while(left <= center){ // 把左边剩余的数移入数组
temp[third++] = arr[left++];
}
// 把新数组中的数覆盖arr数组
while(tmp <= right ){
arr[tmp] = temp[tmp++];
}
}
6.2 非递归排序
7、快速排序
算法实现:
/**
* 快速排序
* @param args
*/
public static void quickSort(int[] arr){
qSort(arr,0,arr.length-1);
}
public static void qSort(int[] arr, int low, int high) {
int pivot=0;
if(low < high){
pivot = partition(arr,low,high);
qSort(arr,low,pivot-1);
qSort(arr,pivot+1,high);
}
}
public static int partition(int[] arr, int low, int high) {
int pivotKey = arr[low];
while(low < high){
while(low < high && arr[high] >=pivotKey ){
high--;
}
swap(arr,low,high);
while(low < high && arr[low] <= pivotKey){
low++;
}
swap(arr,low,high);
}
return low;
}
-----------------------优化---------------------
public static void quickSort1(int[] arr) {
qSort1(arr, 0, arr.length - 1);
}
public static void qSort1(int[] arr, int low, int high) {
int pivot = 0;
// 优化递归操作
// if(low < high){
while (low < high) {
pivot = partition1(arr, low, high);
qSort1(arr, low, pivot - 1);
// qSort1(arr,pivot+1,high);
low = pivot + 1;
}
}
public static int partition1(int[] arr, int low, int high) {
// 优化选取枢轴
int mid = low + (high - low) / 2;
if (arr[low] > arr[high]) {
swap(arr, low, high);
}
if (arr[low] > arr[mid]) {
swap(arr, low, mid);
}
if (arr[mid] > arr[high]) {
swap(arr, mid, high);
}
int pivotKey = arr[low];
// 优化不必要的交换
int temp = pivotKey;
while (low < high) {
while (low < high && arr[high] >= pivotKey) {
high--;
}
// 优化不必要的交换
// swap(arr,low,high);
arr[low] = arr[high];
while (low < high && arr[low] <= pivotKey) {
low++;
}
// 优化不必要的交换
// swap(arr,low,high);
arr[high] = arr[low];
}
arr[low] = temp;
return low;
}