原理
赫夫曼编码可以很有效地压缩数据: 通常可以节省20%-90%, 具体的压缩率依赖于数据的特性;
若将待压缩数据看做是字符序列, 根据每个字符的出现频率, 赫夫曼贪心算法构造出字符的最优二进制表示, 即霍夫曼编码.
二进制字符编码(binary character code, 简称编码 code ), 即每个字符用唯一 的二进制串表示, 这个二进制串也称为码字(codeword).
编码可以分为定长编码(fixed-length code)和变长编码(variable-length code).
定长编码采用固定长度的码字表示字符; 变长编码对不同字符, 采用不同长度的码字, 其思想是通过赋予高频字符短码字, 赋予低频字符长码字, 从而达到比定长编码更好的压缩率.
前缀码(prefix code)是一种典型的变长编码, 这种编码方式中没有任何码字是其他码字的前缀.
任何二进制字符码的编码过程(encoding)都很简单, 只要将表示每个字符的码字连接起来,即可完成数据的压缩;
前缀码的作用是简化解码过程(decoding), 这是由于没有码字是其他码字的前缀, 编码数据的开始码字是无歧义的. 只要简单地识别出开始码字, 将其转换为原字符, 然后对编码数据的剩余部分重复这种解码过程.
为了容易截取开始码字, 解码过程需要以某种方便形式表示前缀码. 这里采用二叉树表示前缀码, 其叶节点为给定字符. 字符的二进制码字用从根节点到该字符叶节点的简单路径表示.
数据的最优编码(optimal code)方案总是对应着一棵满二叉树(full binary tree). 可以采用反证法证明: 若某个最优编码不是满二叉树, 则存在某个内部结点, 有空的左子树或右子树, 此时, 如果将这个内部结点的编码直接设置为非空的右子树或左子树的编码, 这样会使经过这个内部结点的所有字符码字长度少1, 可获得比当前假设的最优编码树, 与原假设矛盾, 所以最优编码总是对应着一棵二叉树.
若 C 为字母表, 且每个字符出现的频率均为正数, 则最优前缀码对应的满二叉树恰有 |C| 个叶节点, 每个叶节点对应字母表中的一个字符, 且恰有 |C| - 1个内部结点. 证明方法采用不同思路计算满二叉树结点总数, 从而得到叶节点和内部结点的数量关系: 首先定义结点的度的概念, 在有根树中,一个结点的孩子结点的个数称为该结点的度.满二叉树的结点总数一方面可以表示为度为0的结点数 n0 +度为1的结点数n1 + 度为2 的结点数 n2, 即 n0 + n1 + n2;另一方面,结点总数可以表示为度为1的结点的孩子结点数 n1 + 度为2 的结点的孩子结点数 2 * n2 + 1(不属于任何结点的孩子的根节点),即n1 + 2 * n2 + 1 , 所以有 n0 + n1 + n2 = n1 + 2 * n2 + 1, 从而有 n0 = n2 + 1, 而度为 0 的结点也就是叶子结点, 即 n0 为叶子结点的个数, 在满二叉树中, 不存在度为 1 的结点, 只有度为 2 的结点, 即 n2 为满二叉树的内部结点的个数, 如此,就证明了对于满二叉树, 内部结点数比叶子结点少 1.
给定一棵对应前缀码的树 T ,可以很容易地计算出编码一个数据或文件所需的二进制位数. 例如对于字母表 C 中的每个字符 c , 令属性 c.freq 表示 c 在文件或数据中出现的频率, 令 dT(c) 表示 c 的叶节点在树中的深度(根节点的深度为 0), 同时也表示字符 c 的码字的长度.编码文件或数据需要的二进制位数为
B(T) 也被定义为树 T 的代价(cost).
赫夫曼算法的伪代码, 如下所示
上图的伪代码中, 假定 C 是一个 n 个字符的集合, 而其中的每个字符 c 都是一个对象, 其属性 c.freq 为字符 c 出现的频率. 算法自底向上构造出最优编码的二叉树 T. 它从|C|个叶节点开始, 执行|C|-1个"合并"操作创建出最终的二叉树. 具体来说, 算法使用一个以属性 freq 为关键字的最小优先队列Q, 以识别两个最低频率的对象, 然后将其合并为一个新节点,并替代它们. 当合并两个对象时, 得到的新对象的频率设置为原来两个对象的频率之和. 经过 |C|-1 次的合并后, 返回优先队列Q中唯一结点, 即编码树的根节点.
C++ 实现
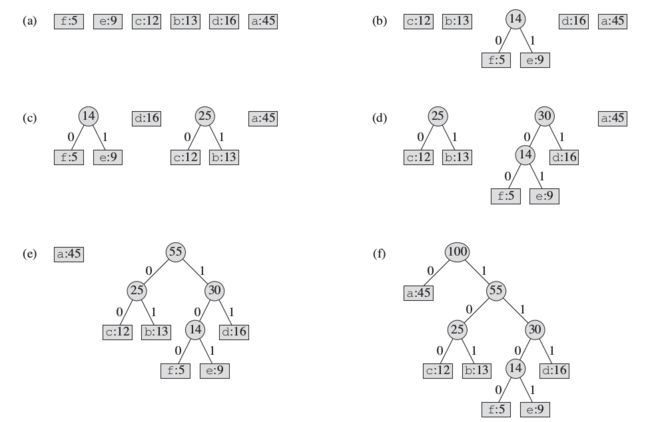
假定输入为 100 个字符的文件, 只含有 {'a', 'b', 'c', 'd', 'e', 'f'} 6 个字符, 'a' - 'f' 出现的频率为 45, 13, 12, 16, 9, 5. 为了简化, 程序中采用数组形式表示,即 {45, 13, 12, 16, 9, 5} , 按伪代码实现的赫夫曼贪心算法对给定输入的具体步骤, 如下图所示
 采用 C++ 2011 编译器, 具体的 C++ 实现代码, 如下
采用 C++ 2011 编译器, 具体的 C++ 实现代码, 如下
/*
Implementation of Huffman greedy algorithm based the huffman algorithm pseudocode in "Introduction to Algorithms, Third Edition"
author: klchang
date: 2020.6
*/
#include
#include
#include
struct Char {
char ch;
unsigned int freq;
Char(char c, int fq): ch(c), freq(fq) {}
Char(): ch(0), freq(0) {}
};
typedef struct BinaryTreeNode BinaryTreeNode;
struct BinaryTreeNode {
Char c;
BinaryTreeNode* left;
BinaryTreeNode* right;
BinaryTreeNode(): c(), left(nullptr), right(nullptr) {}
};
bool operator<(const BinaryTreeNode& lhs, const BinaryTreeNode& rhs)
{
return lhs.c.freq < rhs.c.freq;
}
bool operator>(const BinaryTreeNode& lhs, const BinaryTreeNode& rhs)
{
return lhs.c.freq > rhs.c.freq;
}
template
T* extract_min(std::priority_queue, std::greater >& pq)
{
if (pq.empty()) {
std::cout << "Empty priority queue!" << std::endl;
return nullptr;
}
T* pnode = new T(pq.top());
pq.pop();
return pnode;
}
BinaryTreeNode* huffman(std::vector& charset)
{
// Get the number of chars in charset
int n = charset.size();
// Construct priority queue (min heap) for char set
std::priority_queue, std::greater> pq;
for (std::vector::iterator it = charset.begin(); it != charset.end(); ++it) {
BinaryTreeNode node;
node.c.ch = it->ch;
node.c.freq = it->freq;
pq.push(node);
}
// Get non-leaf and leaf nodes:
// get the lowest two frequencies objects, then merge them, and insert the merged object into pq
for (int i = 0; i < n-1; i++) {
BinaryTreeNode z;
BinaryTreeNode* x = extract_min(pq);
BinaryTreeNode* y = extract_min(pq);
z.left = x;
z.right = y;
z.c.freq = x->c.freq + y->c.freq;
pq.push(z);
}
return extract_min(pq);
}
// Use post-order traverse to deallocate BinaryTreeNode memory
void deallocate_memory(BinaryTreeNode* &root)
{
if (root) {
if (root->left)
deallocate_memory(root->left);
if (root->right)
deallocate_memory(root->right);
delete root;
root = nullptr;
}
}
void print_binarytree(const BinaryTreeNode* root, int order=0)
{
if (root != nullptr) {
if (order == 0) // preorder traverse
std::cout << root->c.freq << ' ';
if (root->left != nullptr)
print_binarytree(root->left, order);
if (order == 1) // inorder traverse
std::cout << root->c.freq << ' ';
if (root->right != nullptr)
print_binarytree(root->right, order);
if (order == 2) // postorder traverse
std::cout << root->c.freq << ' ';
}
}
int main()
{
unsigned int table[] = {45, 13, 12, 16, 9, 5};
int n = sizeof(table)/sizeof(table[0]);
std::vector charset;
for (int i = 0; i < n; i++) {
charset.push_back(Char('a'+i, table[i]));
}
BinaryTreeNode* root = huffman(charset);
std::cout << " preorder sequence of huffman binary tree: " << std::endl
<< '\t';
print_binarytree(root);
std::cout << std::endl;
std::cout << " inorder sequence of huffman binary tree: " << std::endl
<< '\t';
print_binarytree(root, 1);
std::cout << std::endl;
// Deallocate all memory
deallocate_memory(root);
std::cin.get();
return 0;
}
参考资料
[1] (美)科尔曼(Cormen, T.H.)等著,殷建平等译. 算法导论(原书第3版). 北京: 机械工业出版社, 2013.1

