Percolation（渗透模型）普林斯顿算法课

第一周算法课：完成一个渗透模型算法。 

源代码已传github：https://github.com/KevinIRIS/Percolation

我们使用一个N*N的矩阵构造一个渗透系统：

渗透模型说明(背景)：

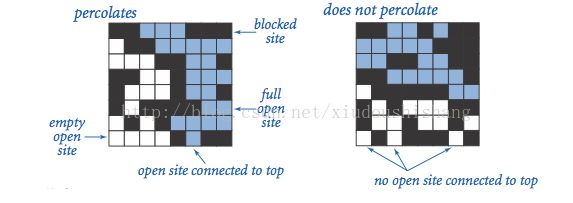
         有一个N*N矩阵，如上图，每个小格子代表一个site，当site为black时说明当前site为blocked(关闭的),非黑色为open,当一个site为open且他和其他相邻的site连接并且可以连接到矩阵顶部我们称这个site为full，如果矩阵最底部有site可以连接到矩阵顶部，我们称这个矩阵为渗透的。

 

编程作业的要求则是实现这么一种模型，并计算出每次模型渗透时，开启区域占总区域个数的百分比，这个百分比近似于某一常数，通过多次模拟采样计算该常数。(当前只实现渗透模型百分比还没有实现)

 

变量： 1、grid ：N*N一维数组表示渗透模型 2、status：N*N 代表每个site的状态 true代表打开  false代表关闭

 

最主要的函数就是open操作，其要考虑四周是否可以连接，流程在下边，希望对大家有用。

 

Public Percolation(int N)  //create N-by-N grid, with all sites blocked

                    初始化  status全部false

                   思想：算法课给的要求是：                              

                    为了方便计算我们grid数组的grid[0]不使用，所以我们初始化一个 N*N+1一维数组

public void open(int i, int j)  //open site (row i, column j) if it is not already  注意：在与四周的site连通，如果四周的site是open状态，则与之连接。

使用weighted quick-union 算法时，需要考虑大小树问题。

public boolean isOpen(int i, int j)   // is site (row i, column j) open

                    根据status数组判断

public boolean isFull(int i, int j)      // is site (row i, column j) full?

           寻找当前site的root节点，如果root节点为矩阵第一行中的一个site，返回true.

public boolean percolates()              // does the system percolate?

           扫描最后一行，如果至少存在一个site为full，则说明此系统为可渗透的，否则不可渗透。

问题延伸：

背景：既然可以计算一个矩阵的渗透率，那我们需要思考一下，当N趋近于无穷时，矩阵的渗透率是否趋近于一个定值即随机open矩阵的sites当矩阵渗透时，sites的open数量占site总数(N*N的比例是否是趋近于一个定值)，事实上当N足够大时，sites的open数占到所有总数的约0.593时这个模型就是渗透的

为了验证这个结果，我们利用名为蒙特卡罗模拟的东西来验证这个结论。

首先初始化一个N*N矩阵，全部为blocked。

重复以下动作直到这个矩阵渗透为止：

         从blocked状态的sites中随机选择一个site将其open，直到当前模型渗透为止。

然后计算open状态的sites的个数设为number，利用number/(N*N)计算出渗透率。

 

重复T次上述过程：

利用方差和平均值思想找出置信率为95%的阀值

public class PercolationStats {

   public PercolationStats(int N, int T)                             // 初始化 并计算相关数值

   public double mean()                               //求阀值的平均数

   public double stddev()                                //其渗透率的标准差

   public double confidenceLow()                          // 最低置信度

   public double confidenceHigh()                          // 高置信度

   public static void main(String[] args)                        //测试代码

}

我的思想比较笨，就是在打开一个site时计算是否渗透，如果没有渗透继续循环直到模型渗透以后。

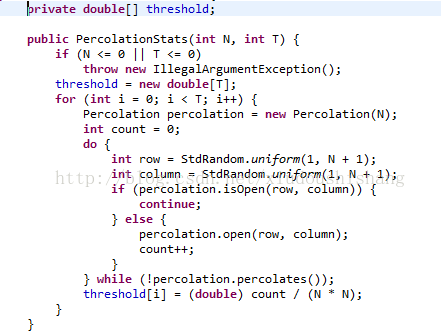
改进思想：

因为当open数小于N时不可能渗透所以这方面可以优化。

其他方面还在想，随时更改。