决策树ID3、C4.5、C5.0以及CART算法之间的比较-并用scikit-learn决策树拟合Iris数据集

引言

在这篇文章中，我主要介绍一下关于信息增益，并比较ID3、C4.5、C5.0以及CART算法之间的不同，并给出一些细节的实现。最后，我用scikit-learn的决策树拟合了Iris数据集，并生成了最后的决策树图片

信息增益（information gain (IG)）

在介绍信息增益之前，我想先介绍3种不纯度的度量手段，它们分别是 Gini index(IG)、entropy(IH)、classification error(IE)

下面，我先介绍熵（entropy）的定义如下：

IH(P)=−∑i=1npi×log(pi)

• P:给定样本下的概率分布P=(p1,p2,p3,…,pn)

假设我们的样本S中只有一个类别，因此我们的概率分布 P=(p1=1)，根据上面的熵公式，我们可以求出IH(P)=1∗log(1)=0 ;假设我们的样本S中只有两个相等数量的类别并服从均匀分布，因此我们的概率分布 P=(p1=0.5,p2=0.5)，根据上面的熵公式，我们可以求出IH(P)=0.5∗log(0.5)+0.5∗log(0.5)=1

下面，我给出Gini index的定义：

IH(P)=1−∑i=1np2i

在实际应用中，Gini index和熵最终会得到非常相似的结果，因此我们不要花费太多的时间用这个两个不纯度来生成决策树。在下面的所有例子中，我都会用熵作为不纯度度量的手段，Gini index大家了解一下就行了。

下面，我给出分类误差（classification error）的定义：

IE(P)=1−max{p(i)}

通过上面的定义我们可以看出，对于样本类别概率分布的变化很不敏感。在这个标准下，我们的决策树会有较浅的高度。

相信大家已经对不纯度的度量手段有了一定的了解，下面让我来给出信息增益的定义：

IG(Ex,a)=H(Ex)−∑v∈values(a)(|{x∈Ex|value(x,a)=v}||Ex|∗H({x∈Ex|value(x,a)=v}))

• Ex:所有样本的集合
• Attr:所有属性的集合
• H:熵 ， 你也可以指定其它的不纯度度量手段
• value(x,a):样本x（∈Ex）中属性a（∈Attr）的值
• values(a):属性a（∈Attr）所有可能的取值

ID3算法

它的伪代码如下：

ID3 (Examples, Target_Attribute, Attributes)
    Create a root node for the tree
    If all examples are positive, Return the single-node tree Root, with label = +.
    If all examples are negative, Return the single-node tree Root, with label = -.
    If number of predicting attributes is empty, then Return the single node tree Root,
    with label = most common value of the target attribute in the examples.
    Otherwise Begin
        A ← The Attribute that best classifies examples.
        Decision Tree attribute for Root = A.
        For each possible value, vi, of A,
            Add a new tree branch below Root, corresponding to the test A = vi.
            Let Examples(vi) be the subset of examples that have the value vi for A
            If Examples(vi) is empty
                Then below this new branch add a leaf node with label = most common target value in the examples
            Else below this new branch add the subtree ID3 (Examples(vi), Target_Attribute, Attributes – {A})
    End
    Return Root

伪代码来源：https://en.wikipedia.org/wiki/ID3_algorithm#Pseudocode

下面，让我们举个例子来应用一下ID3算法。

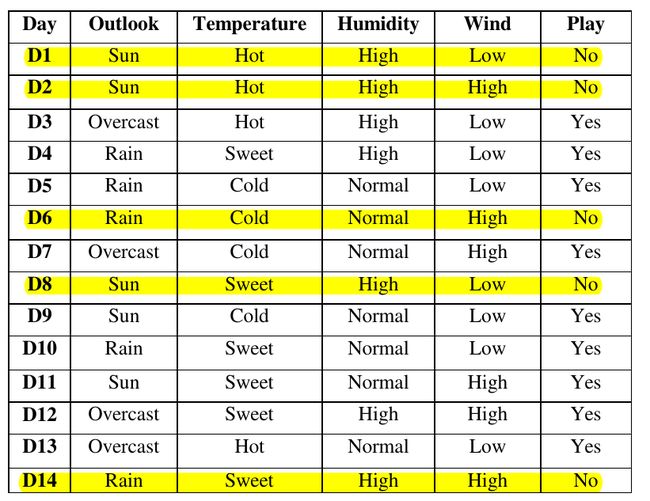
下图为我们的训练集。总共有14个训练样本，每个样本中有4个关于天气的属性，这些属性都是标称值。输出结果只有2个类别，玩(yes)或者不玩(no).

现在，让我们来看看怎么构建决策树的根结点。首先，我们算出整个数据集（S）的熵和按每个属性划分数据集以后的熵。

从数据集上我们可以看出：数据集只有两个类别，它们的概率分布分别为 p1=914和p2=514 ，根据我上面给出的熵公式，可得：

Entropy(S)=−(914∗log2(914)+514∗log2(514))=0.94Entropy(Ssun)=−(25∗log2(25)+35∗log2(35))=0.971Entropy(Sovercast)=−(44∗log2(44)+0∗log2(0))=0Entropy(SRain)=−(35∗log2(35)+25∗log2(25))=0.971

现在，我们已经求出了熵，根据我上面给出的信息增益公式我们就可以求出信息增益了：

IG(S,Outlook)=Entropy(S)−(514∗Entropy(SSun)+414∗Entropy(SOvercast)+514∗Entropy(SRain))=0.246

因此，同样的步骤我们可以求出其它几个信息增益：

IG(S,Wind)=0.048IG(S,Temperature)=0.0289IG(S,Humidity)=0.1515

按照Outlook属性划分获得的信息增益最大，因此我们用这个属性作为我们决策树的根结点。我们不断地重复上面的步骤，会得到一个决策树，如下图：

ID3算法有几个缺点：

• 对于具有很多值的属性它是非常敏感的，例如，如果我们数据集中的某个属性值对不同的样本基本上是不相同的，甚至更极端点，对于每个样本都是唯一的，如果我们用这个属性来划分数据集，它会得到很大的信息增益，但是，这样的结果并不是我们想要的。
• ID3算法不能处理具有连续值的属性。
• ID3算法不能处理属性具有缺失值的样本。
• 由于按照上面的算法会生成很深的树，所有容易产生过拟合现象。

下面，我将引入更加强大的C4.5算法，它可以解决上面的问题。

C4.5算法

对于具有很多值的属性，ID3算法是非常敏感的。而C4.5算法用增益率（Gain ratio）解决了这个问题。在给出增益率的定义之前，我先给出关于内在价值（Intrinsic Value）的定义：

IV(Ex,a)=−∑v∈values(a)|{x∈Ex|value(x,a)=v}||Ex|∗log2(|{x∈Ex|value(x,a)=v}||Ex|)

增益率的定义如下：

IGR(Ex,a)=IG(Ex,a)IV(Ex,a)

假设我们要构建一个决策树来分类公司的客户，那么其中的一个属性可能是客户的信用卡号，这个属性具有很高的信息增益，因为它唯一标识每个客户。但是，我们并不想在决策树中包含这个属性，这是因为它虽然在训练集上表现地很好，而对于没见过的样本它是不可能表现好的。

但是，如果我们用增益率来作为度量的手段，我们可以很好地避免这个问题。也就是说，对于客户的信用卡号这个属性，虽然你的信息增益很大，但是同时你的内在价值也很大，因此你的增益率不会太大。

ID3算法不能处理具有连续值的属性。而C4.5算法很好地解决了这个问题。下面，我举例说明一下它的解决方式。假设训练集中每个样本的某个属性为：{65, 70, 70, 70, 75, 78, 80, 80, 80, 85, 90, 90, 95, 96}。现在我们要计算这个属性的信息增益。我们首先要移除重复的值并对剩下的值进行排序：{65, 70, 75, 78, 80, 85, 90, 95, 96}。接着，我们分别求用每个数字拆分的信息增益（比如用65做拆分：用 ≤65和>65 做拆分，其它数字同理），然后找出使信息增益获得最大的拆分值。因此，C4.5算法很好地解决了不能处理具有连续值属性的问题。

ID3算法不能处理属性具有缺失值的样本。下面的链接非常好地阐述了C4.5算法解决这个问题的方法：https://www.quora.com/In-simple-language-how-does-C4-5-deal-with-missing-values/answer/Aurelian-Tutuianu?srid=IayD
这里我就不在重复这个问题了。

C5.0和CART算法

C5.0是一个商业软件，对于公众是不可得到的。它是在C4.5算法做了一些改进，具体请参考：C5.0算法改进

C5.0主要增加了对Boosting的支持，它同时也用更少地内存。它与C4.5算法相比，它构建了更小地规则集，因此它更加准确。

CART (Classification and Regression Trees)与C4.5算法是非常相似的，但是CART支持预测连续的值（回归）。CART构建二叉树，而C4.5则不一定。

CART用训练集和交叉验证集不断地评估决策树的性能来修剪决策树，从而使训练误差和测试误差达到一个很好地平衡点。

scikit-learn的实现为CART算法的最优版本，详细文档请参考：scikit-learn实现CART

下面，我要用scikit-learn的决策树来分类Iris数据集，让大家体验一下决策树算法的强大！！！

scikit-learn实现决策树分类Iris数据集

代码如下：

from sklearn.datasets import load_iris
from sklearn import tree

iris = load_iris() # 加载Iris数据集
clf = tree.DecisionTreeClassifier()
clf = clf.fit(iris.data, iris.target)


from sklearn.externals.six import StringIO
# 这个需要额外安装，安装方法：https://github.com/erocarrera/pydot，如果遇到问题给我留言
import pydot

dot_data = StringIO()
tree.export_graphviz(clf, out_file=dot_data) 
graph = pydot.graph_from_dot_data(dot_data.getvalue()) 
graph.write_png('iris_simple.png')

上面的代码生成的图片如下：

我们还可以让决策树更加漂亮一些，代码如下：

dot_data = StringIO()  
tree.export_graphviz(clf, out_file=dot_data, feature_names=iris.feature_names, class_names=iris.target_names, filled=True, rounded=True, special_characters=True)  
graph = pydot.graph_from_dot_data(dot_data.getvalue())  
graph.write_png('iris.png')

上面的代码生成的图片如下：