强化学习入门
文章目录
- 前言
- 马尔科夫决策过程(Marcov Decision Processes,MDP)
- 一个简单的例子——Grid World
- MDP的基本概念
- 策略(Policy)
- 另一个例子——Racing
- 折扣(Discounting)
- 求解MDP需要的基本概念
- Value与Q-Value
- 贝尔曼方程(Bellman equations)
- Time-Limited Values
- 值迭代(Value Iteration)
- 策略评估(Policy Evaluation)
- 策略提取(Policy Extraction)
- 策略迭代(Policy Iteration)
- 对比值迭代与策略迭代
- 小结
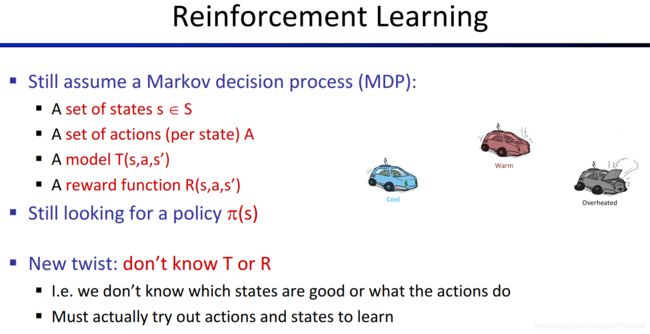
- 强化学习(Reinforcement Learning,RL)
- 引入——Offline planning与Online planning
- 基本概念
- 对比RL与前面的MDP问题
- 基于模型的RL(Model-Based Learning)
- 免模型的RL(Model-Free Learning)
- 免模型的策略评估
- 思路
- 直接评估(Direct Evaluation)
- 间接评估(Indirect Evaluation)与时间差分学习(Temporal Difference Learning)
- Q-Learning
- 探索(Exploration)与利用(Exploitation)
- epsilon-greedy + Q-Learning
- exploration functions + Q-Learning
- Regret
- 近似Q-Learning
- 补充
- SARSA对比Q-Learning
- 推荐阅读
前言
这是对UC伯克利大学的CS188课程做的笔记,主要是记录要点便于个人复习,建议英文能力好的童鞋看原版视频,或者看完本文后再去看视频,B站地址:https://www.bilibili.com/video/av39548965/ ,看8-11集即可。看的过程会遇到一些前面章节提到的概念,例如minimax、expectimax算法,忽略即可,对于总体理解强化学习并不影响,当然,有空的同学建议从头开始看。PPT等更多课程资源见课程的主页:https://inst.eecs.berkeley.edu/~cs188/fa18/
马尔科夫决策过程(Marcov Decision Processes,MDP)
一个简单的例子——Grid World
为了将各个概念解释清楚,这里举一个具体例子——Grid World小游戏。我们规定Grid World的机制是这样的:
里面有一个地图,地图里面有一个机器人,称为Agent(智能体/代理),他每次可以向东南西北四个方向移动一次,每次移动称为一次action(行动)。
地图内还有墙壁、火坑和钻石,撞到墙壁后机器人保持在原来的格子,到达火坑或钻石处之后,下一步只能采取的action是“exit”而不是移动,表示要退出游戏。并且,从火坑处exit会获得惩罚,在钻石处exit会获得奖励(注意,并非从其他格子进入钻石或火坑的reward),我们把惩罚和奖励都称为reward,reward为负数表示惩罚。Agent每次移动也会有一个reward,在本游戏中称为living reward。从一个格子到另一个格子并获得相应的reward的过程,叫做一个time step(时间步)。
Agent的目标,是希望退出游戏时,得到的总的reward越大越好。
Utility:得到的所有(经过折扣的)reward的总和。后面会解释什么是折扣。
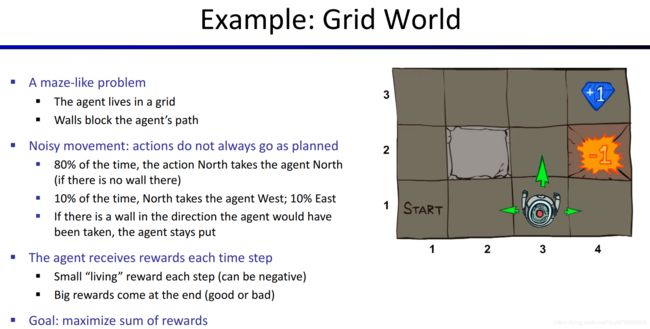
Agent每次选择方向并行动时,行动的结果不一定会和预期一样,例如,Agent打算向北走,但是由于各种随机因素(例如他不小心滑倒了,就相当于没有移动,而不是往北走就一定会到达往北的下一个格子),导致他只有80%的概率真的向北走了一个格子,而还有10%的概率他实际上向西走了一个格子,另外10%概率向东走了一个格子。如下图所示。左边表示action具有确定性。右边表示action具有不确定性,结果是随机的。
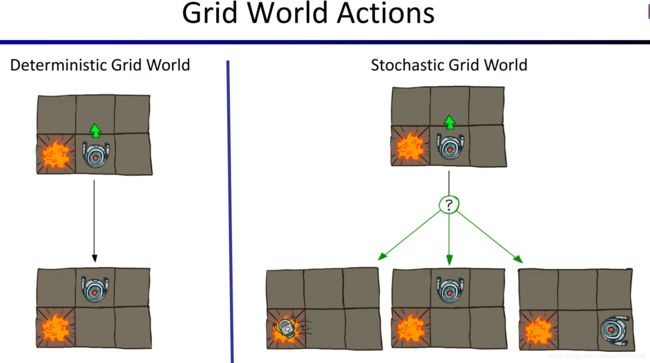
需要指出的是,火坑、钻石、墙壁这些概念只是在Grid World中定义的概念,但“采取行动后从一个状态(格子)到另一个状态(另一个格子)的过程会获得reward”,“action的结果是随机的”,“Agent希望累积的reward越大越好”,“时间步”这些概念,是MDP的通用概念。
MDP的基本概念
一个MDP包含这些量,一个state(状态)的集合 S S S、一个action(行动)的集合 A A A、一个转移函数 T T T(transition function)、一个奖励函数 R R R(reward function)、一个起始状态、还可能有一个终止状态。
T ( s , a , s ′ ) T(\space s, a, s\prime\space ) T( s,a,s′ )表示,当Agent在状态 s s s采取行动 a a a后,他会到达状态 s ′ s\prime s′的概率( s ′ s\prime s′指的是下一个状态),这是一个条件概率。
R ( s , a , s ′ ) R(\space s, a, s\prime\space ) R( s,a,s′ )则表示,当Agent在状态 s s s采取行动 a a a后到达了状态 s ′ s\prime s′,他将获得的reward的值。在实际情况中,这个概率有时仅取决于s,有时仅取决于 s ′ s\prime s′,有时则取决于整个过程( < s , a , s ′ > <\space s, a, s\prime\space> < s,a,s′ >这个序列)

MDP是具有Marcov性质的,指的是下一个状态仅取决于当前状态,而与之前的状态无关。实际上,本文所介绍的MDP中,下一个状态 s ′ s\prime s′取决于当前状态 s s s,采取的行动 a a a,以及转移函数 T T T,不过同样地,与过去的状态无关。
策略(Policy)
如果在MDP中,每次action的结果是确定的,那么我们可以找出一个计划(action的序列),来指导我们从起点走到终点。可惜在MDP问题中,执行action后到达的下一个state可以不确定的,所以我们找不到这样的plan。见 https://www.bilibili.com/video/av39548965/?p=8 (从16:47开始)的演示。
我们在MDP问题中定义另一个与“计划”有类似含义的术语——policy,它表示一个函数 π \pi π,将state映射为action,如果你给policy一个state,它会告诉你应该采取什么action。函数右上角有个星号,表示这个是最优的policy,本文中凡是右上角出现星号,都表示“最优的”。最优的policy指的是,如果Agent按照这个policy的指导来采取action,得到总的reward(即Utility)的期望值将是最大的。
在后文中,我们把寻找一个最优的policy的过程称为“求解MDP”。如果MDP问题的规模(集合S的大小等)比较小,那么我们可以得到一个确定的policy,画出类似下图中Agent拿的指示地图,在程序中,可以用一个map来保存,即每个元素是
 我们来举几个policy的例子,在Grid World中,每一个时间步,执行action后都会得到一个reward,假设除了走到钻石和火坑处,走到其他地方得到的reward都是相同的值,且是一个负值(惩罚)。那么在不同的R函数下,我们会得到不同的 π ∗ \pi^* π∗。如下图所示,+1的格子表示钻石,-1的格子表示火坑,+1和-1表示在该处退出游戏(执行exit动作)的reward。R(s)= - 0.01表示走到下个格子(除了钻石和火坑)的reward是 - 0.01。
我们来举几个policy的例子,在Grid World中,每一个时间步,执行action后都会得到一个reward,假设除了走到钻石和火坑处,走到其他地方得到的reward都是相同的值,且是一个负值(惩罚)。那么在不同的R函数下,我们会得到不同的 π ∗ \pi^* π∗。如下图所示,+1的格子表示钻石,-1的格子表示火坑,+1和-1表示在该处退出游戏(执行exit动作)的reward。R(s)= - 0.01表示走到下个格子(除了钻石和火坑)的reward是 - 0.01。
 这个图的解释见 https://www.bilibili.com/video/av39548965/?p=8(24:11开始)
这个图的解释见 https://www.bilibili.com/video/av39548965/?p=8(24:11开始)
另一个例子——Racing
下图是一个机器车,它想要尽量行驶快一点,但如果加速导致了overheaded(过热),游戏就结束了。
 对于Cool这个状态,我们可以画出一棵搜索树(search tree)来表示从状态Cool开始,未来所有可能的情况。以cool作为树的根,左分支表示slow(减速),右分支表示Fast(加速),每个分支到达的绿色结点是一个临时状态,它又会分出多个状态,表示采取这个action可能导致的不同结果。
对于Cool这个状态,我们可以画出一棵搜索树(search tree)来表示从状态Cool开始,未来所有可能的情况。以cool作为树的根,左分支表示slow(减速),右分支表示Fast(加速),每个分支到达的绿色结点是一个临时状态,它又会分出多个状态,表示采取这个action可能导致的不同结果。
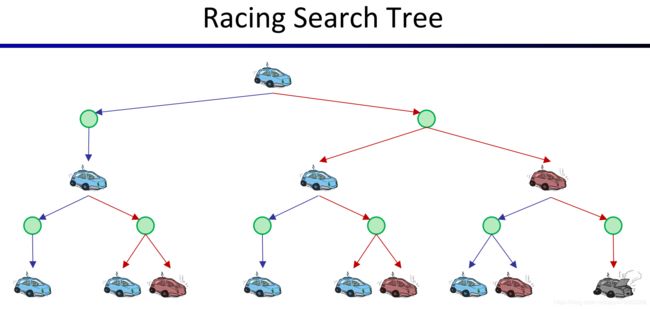 如果看过之前的视频,有些人会觉得可以用expectimax search tree来求解,但上面这个图其实还没画完,如果继续画下去,我们会得到一颗无限大的树,且树的规模随着深度的加深呈指数级增长,如下图所示。所以希望用expectimax search tree来求解MDP问题是不可行的,所以我们需要针对MDP开发其他的求解算法。
如果看过之前的视频,有些人会觉得可以用expectimax search tree来求解,但上面这个图其实还没画完,如果继续画下去,我们会得到一颗无限大的树,且树的规模随着深度的加深呈指数级增长,如下图所示。所以希望用expectimax search tree来求解MDP问题是不可行的,所以我们需要针对MDP开发其他的求解算法。

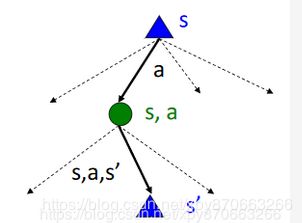
对于任意一个MDP,我们都可以针对它的某个state来画出一颗搜索树,它与expectimax search tree比较类似。下图解释了结点的含义。状态结点用三角形表示, s s s表示当前状态, s ′ s\prime s′表示下一个状态。需要解释的是中间的绿色结点 ( s , a ) (s,a) (s,a),它表示从状态s,选择行动a后,处于的临时状态,“临时”指的是还没有到达下个状态,以后我们把这个中间状态称为q-state。每个state的多条分支表示Agent在这个状态可以选择多个action(Agent可以主动选择),而每个q-state的多个分支则表示到达这个结点后,可能到达的下一个状态有多种可能。 s , a , s ′ s,a,s\prime s,a,s′这条弧,称为一次transition(转移),每个transition都对应了一个概率(由 T T T函数指定)和一个reward(由 R R R函数指定)。
折扣(Discounting)
Agent总是希望能得到的总的reward越多越好,如果总的reward相同,我们有理由觉得目前的reward对于以后才拿到的reward更有价值,例如reward序列[1, 0, 0]比[0, 0, 1]要好。所以我们采用了“折扣”策略,也就是以后才能得到的reward的价值是要打折扣的。我们希望折扣的结果随着时间呈指数下降,所以取一个 γ \gamma γ,它介于[0, 1],现在假设一个reward本来价值是1,那么如果过一个时间步才得到这个reward,它对于当前state的价值要乘以一个 γ \gamma γ,如果再过一个时间步才能得到,它对于当前state的价值还要再乘以一个 γ \gamma γ,即价值降为 γ 2 \gamma^2 γ2。

为什么需要“折扣”呢?对此有很多不同的解释,例如下图中的一些理由。
求解MDP需要的基本概念
Value与Q-Value
我们先来定义几个概念,它们对于求解MDP得到最优policy会很有帮助。
V ∗ ( s ) V^*(s) V∗(s):state的价值,也称为Value。如果从状态s出发,采取最优的行为,那么Agent将得到的累积reward的期望值。用于衡量state结点的好坏。
Q ∗ ( s , a ) Q^*(s,a) Q∗(s,a):q-state的价值,也称为Q-Value。如果从状态s出发,并采取了行动a,在到达下一状态之后采取最优的行为,那么Agent将得到的累积reward的期望值。用于衡量q-state结点的好坏。
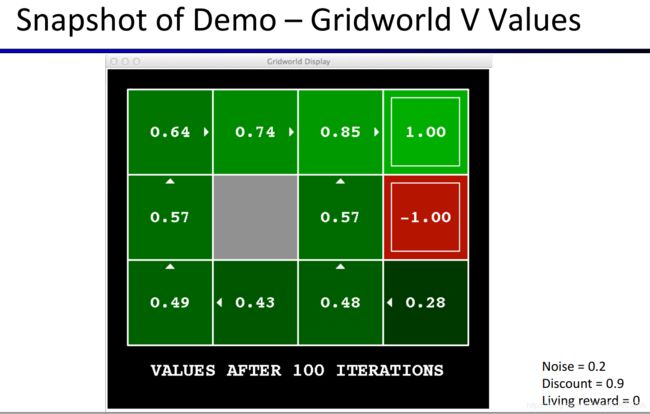
 单从定义来理解state的价值和q-state的价值比较难理解,下图是根据Grid World得到的各个Value,也就是每个state结点(每个格子)的价值。
单从定义来理解state的价值和q-state的价值比较难理解,下图是根据Grid World得到的各个Value,也就是每个state结点(每个格子)的价值。
下图是根据Grid World得到的各个Q-Value,也就是每个q-state结点(每个临时状态,即前文中的绿色结点)的价值。
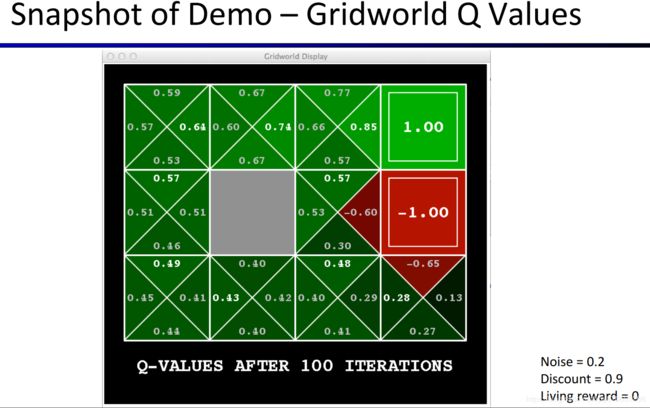
上面两幅图中的数字的含义的解释见 https://www.bilibili.com/video/av39548965/?p=8 (从57:10开始)。此处是对算法运行100次后得到的结果的解释,之后还会对各个Value和Q-Value如何得到的过程做演示和解释。强烈建议将所有与Value和Q-Value相关的解说都看一遍,理解这些Value与Q-Value代表什么含义,又是如何得到的。
贝尔曼方程(Bellman equations)
我们可以将Value和Q-Value的定义用数学的语言来表达,如果觉得下面图中的公式难以理解,可以参考视频讲解。强烈建议看一下视频,因为后面会不断用到这几个公式。 https://www.bilibili.com/video/av39548965/?p=8 (从60:51开始)。这些方程的思想非常非常重要,它们是求解MDP问题的基础,之后提出的多个算法都是基于Bellman方程的。

前面在介绍Racing那个例子时,我们说对于这个问题没办法用expectimax search tree来求解,因为得到的搜索树是无穷大的,而且其中有很多子树其实是完全一样的,所以工作量过大而且有大量重复的工作。那如果我们将这棵树直接截断,使高度降低一点,例如只要前100层,那不就可以了吗,毕竟深度越深,由于折扣 γ \gamma γ机制,后面那些子结点对于根结点的值应该是贡献不大的。那么我们怎么具体利用这个思想呢,先来看Time-LImited Values这个关键的概念。
Time-Limited Values
V k ( s ) V_k(s) Vk(s):如果Agent只剩下k个时间步,游戏就要结束了(Agent被强制退出MDP),在这种前提下求得的Value。
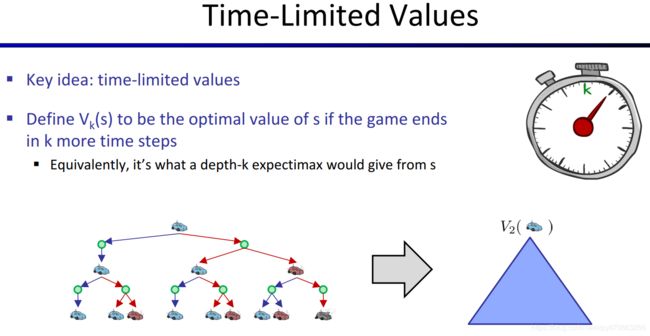
对于这个概念的理解非常重要,见视频的Demo与解释 https://www.bilibili.com/video/av39548965/?p=8 (69:41开始)。从这个Demo中我们还可以看到,对于每个k值,我们算出每个state的 V k ( s ) V_k(s) Vk(s)后,根据这些值绘制地图,我们就可以找到一个当前k值对应的最优policy,也就是对于每一个state,只需环顾四个方向,在相邻的state中找到 V k ( s ) V_k(s) Vk(s)最大的即可知道应该往哪里走。如下图所示,图中的小箭头就是policy的形象的描述,即告诉Agent在每个state(格子)应该采取什么action(走哪个方向)。
![]()
从Demo中,我们还可以发现一个非常重要的现象,随着k值增大,每个格子的 V k ( s ) V_k(s) Vk(s)仍然有一些微小的变化,但表明policy的那些小箭头已经不变了。我们设计算法是为了找到最优的policy,所以其实policy趋于稳定我们的算法就可以终止,这是一个重要的优化算法的思路,后文会再提到。
值迭代(Value Iteration)
Value Iteration(值迭代)算法是一个用于求解MDP问题,得到其最优的policy的算法。算法开始时,设置每个结点的 V 0 ( s ) V_0(s) V0(s)为0,然后根据下图的更新公式来更新 V k + 1 ( s ) V_{k+1}(s) Vk+1(s),直到Value不变(或几乎不变)。下图中的更新公式,也称为Bellman Update。
怎么知道根据这个更新公式来迭代k次后,Value一定会收敛、值迭代算法一定会停机呢,又怎么确定收敛后,根据Value得到的policy就是最优的policy呢?事实上,这涉及到动态规划(Dynamic Programming)以及不动点法的知识,感兴趣的同学可以查阅相关资料。

也就是说,对于更新公式中的 V k + 1 ( s ) V_{k+1}(s) Vk+1(s)等带下标的Value值,可以不用前面说的Time-Limited Values来理解,而如果熟悉不动点法,我们可以直接证明根据这个更新公式来迭代,可以得到Bellman方程的不动点。下面给出一个证明,仅供参考。
策略评估(Policy Evaluation)
策略评估(Policy Evaluation)指的是,对于一个给定的Policy(告诉你在每个state应该采取哪个action),求出每个state的Value。这其实和值迭代算法有点类似(都是求state的Value),但是对应的search tree却简单很多。如下图所示。
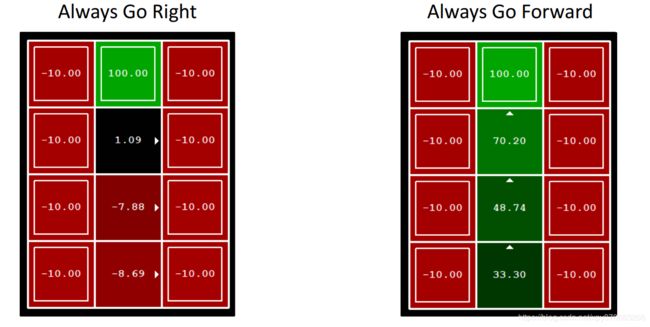
下面是一个例子,对于Grid World有两个policy,第一个告诉agent,总是往右走,另一个告诉agent,总是往前走。
求解出来的结果如下图所示(后面会解释怎么算出来的)
策略评估的关键概念如下图所示。红框中的是Policy Evaluation中的Bellman方程。
(Bellman方程并不是特定的一组或一个方程,在MDP问题的各个算法中,用这种递归定义的思路得到的类似形式的方程都叫Bellman方程)

同样地,我们可以用值迭代算法中使用的不动点法来求解这个递归式的不动点,只需要将Bellman Equation转化成Bellman Update。不过,这里的Bellman方程是一个线性方程组(值迭代算法的Bellman方程由于含有max函数所以不是线性方程组),可以直接用矩阵工具来解决,例如用Matlab来求解。如下图所示。
策略提取(Policy Extraction)
策略评估是输入一个策略,得到一组Value(每个state的Value),而策略提取(Policy Extraction)则相反,它能根据给出的每个state的Value,输出其对应的策略。下图的 a r g m a x argmax argmax函数指的是求函数的最大值点,即对应于最大值(最大Utility)的自变量a(action)。

另外还有一种策略提取算法,是根据Q-Values来提取Policy,它比根据Value来提取策略要简单很多,如下图所示。值得注意的是, a r g m a x argmax argmax函数后面的其实就是Q-Value的定义,即 Q ( s , a ) Q(s, a) Q(s,a)函数。记得这里,后面看到Q-Learning算法再回顾下这里。

策略迭代(Policy Iteration)
在提出策略迭代算法之前,我们先来看一下值迭代算法有哪些缺陷。如下图所示。

为此,我们提出一个另一个用于求解MDP得到最优策略的算法——策略迭代。下图是策略迭代的基本思想,在初始化policy后,开始迭代,每次迭代分为两步,第一步是使用之前的策略评估算法对当前的policy进行评估,然后是对Policy进行改进。
用数学语言描述Policy Iteration算法,如下图所示。(教授讲到这里还说大家看到这里很可能会感受到Symbol Shock,也就是看对那么多符号感到懵逼,心想,哇好多V好多π好多Q。。。这教授真的好逗,建议大家去看看视频)
对比值迭代与策略迭代
Value Iteration和Policy Iteration都是求解最优Policy的方法,下图对比了这两个算法。
- 它们都是在计算每个state的最优Value。
- 在值迭代中,每次迭代都更新了Value和Policy(对Policy的更新是隐式的,我们并没有保存Policy,所以并不是直接更新,但是我们每次对a产生的Utility求max的操作,本质上是一个能更新Policy的操作)
- 在策略迭代中,我们先用策略评估算法得到各个Value,这个过程对比值迭代来说快很多,因为每个state要采取的action都是被policy指定的,不用考虑所有action,即没有max函数。策略评估后,我们想办法完善这个policy。
- 这两个方法都是在用动态规划的思想来解决MDP问题。
小结
对MDP中涉及到的算法的小结
强化学习(Reinforcement Learning,RL)
引入——Offline planning与Online planning
PS:强化学习中也有一对经典的概念,Online与Offline,但与本小节中的不同。
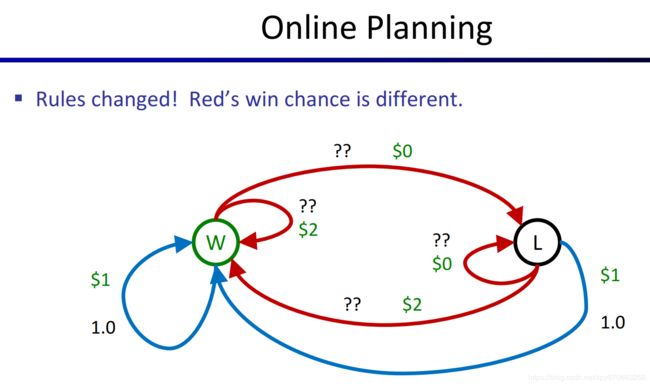
我们先来看另一个MDP的例子——双老虎机游戏。其中蓝色的老虎机,每次摇都会得到1美元,而红色的老虎机,每次有75%的概率会给你2美元,有25%概率会给你0美元。
这个问题可以用MDP来描述,得到下图。
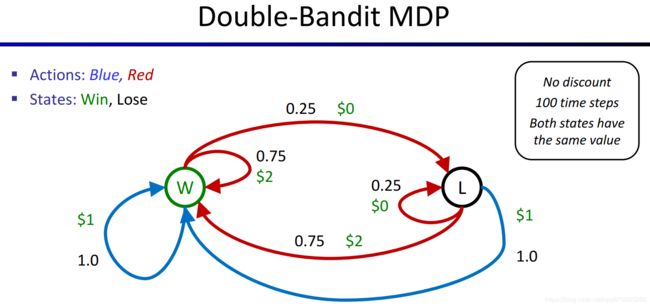
在前文,我们提出了一些可以解决MDP问题的算法,用于找到最优的Policy,这里同样适用。这些根据各种信息( T T T函数和 R R R函数)求解MDP的过程,我们称为Offline Planning(离线规划),下图具体解释了这个概念。
那假如我们不知道MDP的一些关键参数,例如 T T T函数(见前文),那我们该怎么求解MDP问题?例如上面的老虎机问题中,假如我们并不知道红色老虎机有多大概率给我们2美元或0美元,这个问题就不能用之前的方法来求解了。
但是,你可以不断尝试,例如,你试了十次蓝色的老虎机,它每次都给你1美元,然后你可能想试一下红色的,说不定那台老虎机给你更多,试了十次你发现,平均下来,这个红色的老虎机每次给你的钱比1美元少的多,那你就会想,那我不如去摇蓝色的老虎机算了。有时你又会想,会不会是我摇的那几次刚好摇到比较少钱的情况呢?我用不用再回去摇几次红色的看看它究竟平均下来能给我多少美元?但是去摇红色的是要冒一定风险的,因为根据你的经验,你知道蓝色的老虎机每次都给你1美元,而红色的老虎机给你的要少的多。
这个过程,就是Reinforcement Learning(RL),并且涉及了一些重要的RL中的概念,见下图的解释。
 前面的部分写的比较详细,可以了解到RL的基本概念,后面的部分写省略一点,因为太耗时了,建议大家看原视频
前面的部分写的比较详细,可以了解到RL的基本概念,后面的部分写省略一点,因为太耗时了,建议大家看原视频
基本概念
对比RL与前面的MDP问题
前面的MDP问题最大的特点是我们知道了MDP问题中的最关键的因素——T函数和R函数,因此可以采用值迭代、策略迭代算法来求最优策略,但RL中,我们并不知道 T T T或 R R R,用不了这些算法,所以我们需要不断地尝试,不断地学习。前者在已知完整的MDP模型的情况下,直接求解出最优策略(而不需要Agent与Environment的实际交互)的过程,是一个Offline的过程,而RL中Agent与Environment不断交互,在不断尝试中学习,逐渐优化策略的过程称为Online的过程。
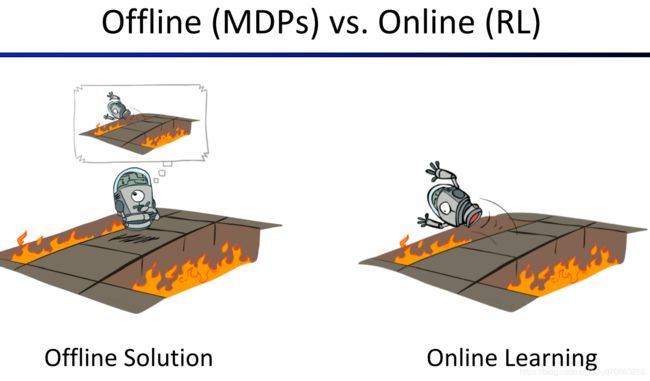
如何在不知道 T T T和 R R R的情况下求解处最优的策略 π ∗ \pi^* π∗呢?有两种思路,Model-Based的方法与Model-Free的方法。
基于模型的RL(Model-Based Learning)
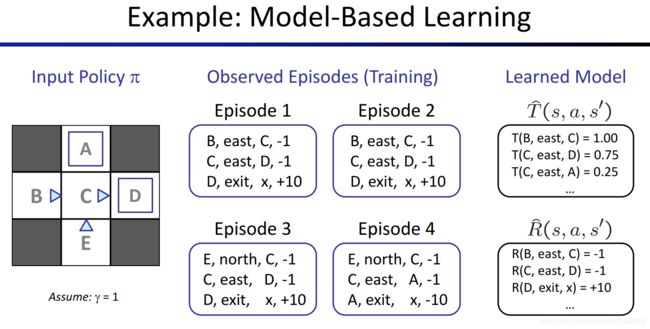
总体思路:通过不断尝试,Agent可以根据经验对 T T T和 R R R进行估计,由估计出的 T ^ \hat{T} T^和 R ^ \hat{R} R^来建立MDP问题,然后问题就转化为已知完整MDP问题的情况,就可以用值迭代、策略迭代等算法了。
我们把Agent每次从起始状态到终止状态的一次探索过程称为Episode,下图展示了Agent如何从多个Episode中估计出 T T T和 R R R,具体解释见https://www.bilibili.com/video/av39548965/?p=10(20:06开始)。
免模型的RL(Model-Free Learning)
我们先来看如何在没有 T T T和 R R R的情况下,进行Policy Evaluation,即评估每个state的Value。
免模型的策略评估
思路
相信大家都学过概率论与数理统计的基本内容,假如现在有一个问题,我们希望统计一下某个市所有居民的年龄的平均值,那么我们的思路是什么?
第一种思路,我们认为所有居民的年龄分布服从某个分布 T ( θ ) T(\theta) T(θ),其中 θ \theta θ为该分布的参数,那么我们可以利用参数估计的方法对参数 θ \theta θ进行估计,从而得到这个分布 T ( θ ) T(\theta) T(θ)分布律(若换为连续型随机变量则对应概率密度函数),这就相当于一个模型,然后,我们可以求出这个分布的期望,即可作为对所有居民的平均年龄的估计。
第二种思路,我们可以随机采样,得到一个较小的样本(例如1000人)后,直接调查他们每个人的岁数,然后求均值,将结果作为对所有居民平均年龄的估计。
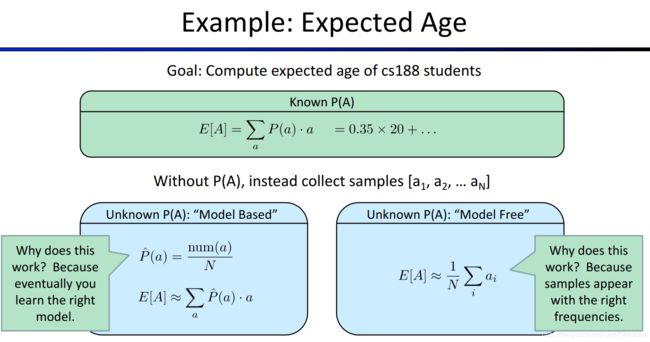
从第一种思路到第二种思路的转换,就是Model-Based到Model-Free的关键,因为用后一个思路,可以将Bellman Update中的 T T T函数给去掉,后面再详细介绍是什么意思。
下面这个图,是课程中的教授给的例子,和我举的例子其实差不多。
直接评估(Direct Evaluation)
Agent采样得到多个Episode后,利用Value的定义直接用对每个state计算Value,然后对每个Episode得到的结果求均值。

详细的计算过程有利于理解,见下图,或见演示过程https://www.bilibili.com/video/av39548965?p=10(从36:50开始)
直接评估的缺陷有很多,例如在数据量不大时,很容易出现估计不准确的情况,当然这个缺点在采集的数据足够多时会得到改善和解决,但我们希望RL能快速学习,而不是在长时间的收集数据之后才有明显改善。其他优缺点见下图。
间接评估(Indirect Evaluation)与时间差分学习(Temporal Difference Learning)
直接评估没有考虑到各个state之间的联系,如果使用Bellman方程,就可以在计算过程将各个state联系起来,但是关键问题在于,策略评估使用的Bellman Update中,需要使用 T T T和 R R R,我们怎样才能在不知道 T T T和 R R R的情况下完成Bellman Update呢?

我们可以使根据前面提到的思路,提出一种基于采样的策略评估的方法。如下图所示,我们得到对于某个state的多个样本,直接求均值即可。这种方法中的样本是从该状态 s s s到特定的下个状态 s ′ s\prime s′的reward是多少(其实就是R函数的一个点),我们记录这些reward即可,而更新需要的 γ \gamma γ由算法确定, V k π ( s ′ ) V^\pi_k(s\prime) Vkπ(s′)则是之前的迭代过程求出来的值。

但问题在于,我们需要得到多个从该状态 s s s到特定的下个状态 s ′ s\prime s′的样本之后才能进行计算,而Environment的不确定性可能导致我们很久才能收集到那么多样本(因为采集到一个 R ( s , π ( s ) , s ′ ) R(s, \pi(s), s\prime) R(s,π(s),s′)后,下一次Agent可能会到达另一个不同的 s ′ s\prime s′)。所以我们希望,每次得到一个Episode之后(里面有多个我们需要的样本,即 R R R函数的一个点),都能利用这个Episode进行一定程度的学习,而不是要在采集大量Episode后才能开始计算,所以我们提出了时间差分学习(Temporal Difference Learning)。
之前我们对多个样本使用平均操作,如果只采集一个样本,要怎样才能对它进行“平均”操作用于更新呢Value呢?下图展示了时间差分法的思路,即设置一个0和1之间的学习率 α \alpha α(learning rate),对于每个state,更新后的Value等于旧的Value与新的样本所反映的Value做加权平均。一般来说我们设置 α \alpha α更靠近0,例如0.1,也就是每次更新都倾向于保持旧的值。对于更新公式,我们还可以变形得到另一个等价的公式,见下图最下方。

时间差分法使用的计算均值的方法其实是指数移动(加权)平均的方法,感兴趣的同学可以查阅相关知识,下面是课程中给出的一些分析,从分析结果可以看出,在离当前时间越近的时候所采集到的样本,对得到的均值的贡献越大。
算法的实际运算过程可以见下图,或看课程的演示 https://www.bilibili.com/video/av39548965?p=10 (从50:27开始),建议与直接评估的Demo对比来看,以分清它们的差异。
Q-Learning
上述的时间差分法可以进行策略评估,得到所有Value值,但是如果要完善Policy就会被卡住,因此我们需要改变一下思路。我们先来回顾Policy Iteration是如何完善Policy的:对于一个状态s,在所有action中,找到最大的Q-Value对应的行动a(即 a r g m a x argmax argmax操作),然后将该state下的最优action更新为a。
如果我们求出的是Value,对于更新Policy没什么帮助,因为更新公式中, a r g m a x argmax argmax函数求的是Q(s, a)的最大值点。所以我们的思路就是,不如直接对Q-Value进行估计(相当于改变了策略评估的思想),得到的结果非常有利于完善Policy。
在这之前Model-free的部分,我们求出的Value并不能直接指导我们的行为,毕竟只是策略评估,并没有进行策略的更新和完善。而如果修改为求出Q-Value,这是可以直接指导我们怎么采取action的(只需要对于某个state,在所有action上做一个argmax操作,看看哪个


对比之前我们提出Value Iteration的思路,现在我们提出Q-Value Iteration。注意,Q-Value Iteration的Bellman Update公式中,最右端的 max a ′ Q k ( s ′ , a ′ ) \mathop{\max_{a\prime}}Q_k(s\prime, a\prime) maxa′Qk(s′,a′)其实就是 V k ( s ′ ) V_k(s\prime) Vk(s′)
Q-Value Iteration与Value Iteration的最大不同在于,它的Bellman Update公式以 Σ T \Sigma T ΣT开头。我们前面说过对于这种情况可以将其修改为基于样本的更新公式,而且基于时间差分法的思路,可以得到只利用一个新样本便可更新的公式。于是,我们就得到了下面的Q-Learning算法。Q-Learning的演示见https://www.bilibili.com/video/av39548965?p=10 (从66:47开始,演有2个Demo),建议看一下,教授还会对其中的一些思想作解释。深度强化学习就是基于Q-Learning的,所以理解好Q-Learning非常重要。

更新公式可以联立去掉sample,并将reward函数简写为r,改成如下形式。
在其他文献中,经常出现的是下面的等价的式子,这个式子中的difference可以形象地理解为“样本(真实值)与当前预测值的差距”,而 α \alpha α也可理解为学习率,就是每次对我们的Q函数进行多少修正。
前面在讲Policy Extraction时,我们就发现,从Q-Value中提取策略比从Value中提取策略要容易很多,所以我们说,在Q-Value Iteration收敛后,最优的Policy已经“编码”在这些Q-Value中了。
接下来是Off-Policy的概念,Q-Learning算法是一个Off-Policy Learning的过程。见下图。
探索(Exploration)与利用(Exploitation)
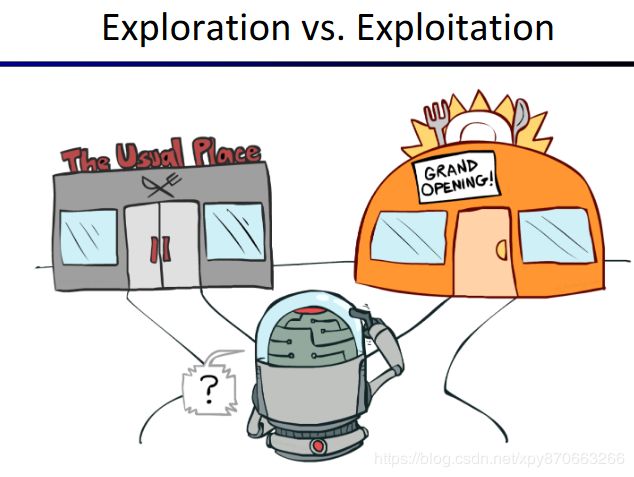
举一个例子,你最喜欢你家附近的餐馆A,但最近你发现了一家新开的餐馆B,你要不要去尝试一下呢?说不定去尝试一下这家新的餐馆可以发现更合你口味的菜肴,这种去尝试Environment中的未知部分的行为就叫探索(Exploration)。而基于现有的消息(A餐馆最合你口味),你应该直接选择A餐馆,这样是最能保证你这餐能吃的好的选择,这就是利用(Exploitation)。
为了解决“探索与利用难题”(Exploration and Exploitation Dilemma),大家经常使用的算法是 ϵ − g r e e d y \epsilon-greedy ϵ−greedy算法。
epsilon-greedy + Q-Learning
取一个介于0和1之间的 ϵ \epsilon ϵ,然后 ϵ \epsilon ϵ的概率采取随机行动(有利于探索),1- ϵ \epsilon ϵ的概率根据Policy来行动,即根据Q表,选择当前状态下,哪个
如果 ϵ \epsilon ϵ取得过大,有一个缺点是,在算法收敛后,Agent仍然以很高的概率随机行动。两种解决方法,一是随着训练时间加长来降低 ϵ \epsilon ϵ,手动或用一个与时间有关的系数来实现。另一个是Exploration Function。
exploration functions + Q-Learning
记录下
Regret
近似Q-Learning
为了运行Q-Learning算法,我们经常用一个Q-Table来保存Q值,但实际生活中的MDP问题,经常会遇到状态数或动作数非常大以至于没办法保存到内存中的情况。因此我们需要Agent学会“泛化”能力,也就是如果已经遇过一种情况,下一次遇到类似的情况也可以处理。例如世界上有无数大楼,机器人已经学会“为了进入大楼A,就要打开门A”,那么见到大楼B时,他就应该能思考到,为了进入大楼B,应该打开门B。
为了达到这种目的,我们要用特征(feature)来表示q-state,即

下图中的 f 1 f_1 f1, f 2 f_2 f2等是特征函数,也就是输入s或
后面的视频我不看了,因为到了这里我觉得自己已经理解为什么可以用深度学习+强化学习了。我的理解是这样的。首先,强化学习可以用Q-Learning来解决,也就是只要得到一个Q-Table即可。而Q-Table可以看作一个函数,输入为q-state(及
![]()
所以明白了监督学习的模型在与强化学习结合的过程中起到什么作用后,我觉得就可以去学习深度强化学习了。(当然,还要了解神经网络/深度学习的基本知识)
补充
SARSA对比Q-Learning
SARSA与Q-Learning一样,都是TD算法,且都是对Q-Value(而不是state的Value)进行估计(下图中的绿色结点)。事实上SARSA与Q-Learning非常相似,它们都使用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy算法来决定在 s s s处应该采取的行为 a a a,而到达 s ′ s\prime s′后,Agent会得到回报 R ( s , a , s ′ ) R(s,a,s\prime) R(s,a,s′),区别在于,如何根据这次转移(Transition)得到的信息(观察到的 r r r和 s ′ s\prime s′)来估计
Q-Learning认为 V ( s ′ ) = max a ′ Q ( s ′ , a ′ ) V(s\prime)=\mathop{\max_{a\prime}}Q(s\prime,a\prime) V(s′)=maxa′Q(s′,a′)(个人认为这的确符合Value的定义),而SARSA认为,应该先用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy算法来决定在 s ′ s\prime s′应采取的行动 a ′ a\prime a′,且认为 V ( s ′ ) = Q ( s ′ , a ′ ) V(s\prime)=Q(s\prime,a\prime) V(s′)=Q(s′,a′)(对比Q-Learning可以发现没有max函数)。
Q-Learning采用的是贪心策略,每次估计 s ′ s\prime s′的Value时都根据当前Policy选择最大Q-Value对应的 a ′ a\prime a′,而SARSA采用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy算法来选择 a ′ a\prime a′,也就是只有1- ϵ \epsilon ϵ的概率是贪心的。
Q-Learning选择的 a ′ a\prime a′只是用来估计 s ′ s\prime s′的Value,进而估计
为了讲清楚一点,对着上面的状态转移图,再小结一下各操作,如下表。
| 算法 | 在 s s s处实际采取的行动 | 对 s ′ s\prime s′的Value进行估计 | 在 s ′ s\prime s′处实际采取的行动 |
|---|---|---|---|
| SARSA | 根据 ϵ − g r e e d y \epsilon-greedy ϵ−greedy得到 | 根据 ϵ − g r e e d y \epsilon-greedy ϵ−greedy得到 a ′ a\prime a′, V ( s ′ ) = Q ( s ′ , a ′ ) V(s\prime)=Q(s\prime,a\prime) V(s′)=Q(s′,a′) | 直接使用估计 s ′ s\prime s′的Value时得到的 a ′ a\prime a′,因此称为On-Policy) |
| Q-Learning | 根据 ϵ − g r e e d y \epsilon-greedy ϵ−greedy得到 | V ( s ′ ) = max a ′ Q ( s ′ , a ′ ) V(s\prime)=\mathop{\max_{a\prime}}Q(s\prime,a\prime) V(s′)=maxa′Q(s′,a′) | 根据 ϵ − g r e e d y \epsilon-greedy ϵ−greedy得到,并非之前求的 a ′ a\prime a′,因此称为Off-Policy |
更多关于On-Policy和Off-Policy的解释,见博客: https://blog.csdn.net/cuihuijun1hao/article/details/83042312
我们可以根据代码来验证上述说法,代码参考自博客(作了部分修改): https://towardsdatascience.com/reinforcement-learning-temporal-difference-sarsa-q-learning-expected-sarsa-on-python-9fecfda7467e
算法伪代码可以见 https://blog.csdn.net/liweibin1994/article/details/79119056
(注意代码中,s_代表 s ′ s\prime s′,a_代表 a ′ a\prime a′)
SARSA的python代码:
import gym
import numpy as np
import time
"""
SARSA on policy learning python implementation.
This is a python implementation of the SARSA algorithm in the Sutton and Barto's book on
RL. It's called SARSA because - (state, action, reward, state, action). The only difference
between SARSA and Qlearning is that SARSA takes the next action based on the current policy
while qlearning takes the action with maximum utility of next state.
Using the simplest gym environment for brevity: https://gym.openai.com/envs/FrozenLake-v0/
"""
def init_q(s, a, type="ones"):
"""
@param s the number of states
@param a the number of actions
@param type random, ones or zeros for the initialization
"""
if type == "ones":
return np.ones((s, a))
elif type == "random":
return np.random.random((s, a))
elif type == "zeros":
return np.zeros((s, a))
def epsilon_greedy(Q, epsilon, n_actions, s, train=False):
"""
@param Q Q values state x action -> value
@param epsilon for exploration
@param s number of states
@param train if true then no random actions selected
"""
if train or np.random.rand() < epsilon:
action = np.random.randint(0, n_actions)
else:
action = np.argmax(Q[s, :])
return action
def sarsa(alpha, gamma, epsilon, episodes, max_steps, n_tests, render = False, test=False):
"""
@param alpha learning rate
@param gamma decay factor
@param epsilon for exploration
@param max_steps for max step in each episode
@param n_tests number of test episodes
"""
env = gym.make('Taxi-v2')
n_states, n_actions = env.observation_space.n, env.action_space.n
Q = init_q(n_states, n_actions, type="ones")
timestep_reward = []
for episode in range(episodes):
print(f"Episode: {episode}")
total_reward = 0
s = env.reset()
# 根据epsilon_greedy来选择在s处的行动a
a = epsilon_greedy(Q, epsilon, n_actions, s)
t = 0
done = False
while t < max_steps:
if render:
env.render()
t += 1
# 从s处执行a,到达s_ 并获得reward
s_, reward, done, info = env.step(a)
total_reward += reward
# 根据epsilon-greedy得到a_, 认为V(s_)=Q(s_,a_)
a_ = epsilon_greedy(Q, epsilon, n_actions, s_)
if done:
# 如果s已经是终止状态(没有s_),根据Q-Value的定义,这次转移的reward就是对处的Q-Value的估计,没有必要再加上gamma * V(s_)(即Q[s_, a_])
Q[s, a] += alpha * ( reward - Q[s, a] )
else:
# 否则,reward + (gamma * Q[s_, a_])才是对处的Q-Value的估计
Q[s, a] += alpha * ( reward + (gamma * Q[s_, a_] ) - Q[s, a] )
# 更新完Q表后,将a_赋给a,即直接将估计s_的Value时得到的a_作为s_处实际采取的行动
s, a = s_, a_
if done:
if render:
print(f"This episode took {t} timesteps and reward {total_reward}")
timestep_reward.append(total_reward)
break
if render:
print(f"Here are the Q values:\n{Q}\nTesting now:")
if test:
test_agent(Q, env, n_tests, n_actions)
return timestep_reward
def test_agent(Q, env, n_tests, n_actions, delay=0.1):
for test in range(n_tests):
print(f"Test #{test}")
s = env.reset()
done = False
epsilon = 0
total_reward = 0
while True:
time.sleep(delay)
env.render()
a = epsilon_greedy(Q, epsilon, n_actions, s, train=True)
print(f"Chose action {a} for state {s}")
s, reward, done, info = env.step(a)
total_reward += reward
if done:
print(f"Episode reward: {total_reward}")
time.sleep(1)
break
if __name__ =="__main__":
alpha = 0.4
gamma = 0.999
epsilon = 0.1
episodes = 3000
max_steps = 2500
n_tests = 20
timestep_reward = sarsa(alpha, gamma, epsilon, episodes, max_steps, n_tests)
print(timestep_reward)
然后是Q-Learning的Python代码:
import gym
import numpy as np
import time
"""
Qlearning is an off policy learning python implementation.
This is a python implementation of the qlearning algorithm in the Sutton and
Barto's book on RL. It's called SARSA because - (state, action, reward, state,
action). The only difference between SARSA and Qlearning is that SARSA takes the
next action based on the current policy while qlearning takes the action with
maximum utility of next state.
Using the simplest gym environment for brevity: https://gym.openai.com/envs/FrozenLake-v0/
"""
def init_q(s, a, type="ones"):
"""
@param s the number of states
@param a the number of actions
@param type random, ones or zeros for the initialization
"""
if type == "ones":
return np.ones((s, a))
elif type == "random":
return np.random.random((s, a))
elif type == "zeros":
return np.zeros((s, a))
def epsilon_greedy(Q, epsilon, n_actions, s, train=False):
"""
@param Q Q values state x action -> value
@param epsilon for exploration
@param s number of states
@param train if true then no random actions selected
"""
if train or np.random.rand() < epsilon:
action = np.random.randint(0, n_actions)
else:
action = np.argmax(Q[s, :])
return action
def qlearning(alpha, gamma, epsilon, episodes, max_steps, n_tests, render = False, test=False):
"""
@param alpha learning rate
@param gamma decay factor
@param epsilon for exploration
@param max_steps for max step in each episode
@param n_tests number of test episodes
"""
env = gym.make('Taxi-v2')
n_states, n_actions = env.observation_space.n, env.action_space.n
Q = init_q(n_states, n_actions, type="ones")
timestep_reward = []
for episode in range(episodes):
print(f"Episode: {episode}")
s = env.reset()
t = 0
total_reward = 0
done = False
while t < max_steps:
if render:
env.render()
t += 1
# 根据epsilon_greedy来选择在s处的行动a
a = epsilon_greedy(Q, epsilon, n_actions, s)
# 从s处执行a,到达s_ 并获得reward
s_, reward, done, info = env.step(a)
total_reward += reward
"""区别"""
# 根据Q表选择在当前s下带来最大Q-Value的a_, 认为V(s_)=Q(s_,a_)
a_ = np.argmax(Q[s_, :])
if done:
# 见sarsa代码中此处的注释
Q[s, a] += alpha * ( reward - Q[s, a] )
else:
# 见sarsa代码中此处的注释
Q[s, a] += alpha * ( reward + (gamma * Q[s_, a_]) - Q[s, a] )
s = s_
if done:
if render:
print(f"This episode took {t} timesteps and reward: {total_reward}")
timestep_reward.append(total_reward)
break
if render:
print(f"Here are the Q values:\n{Q}\nTesting now:")
if test:
test_agent(Q, env, n_tests, n_actions)
return timestep_reward
def test_agent(Q, env, n_tests, n_actions, delay=1):
for test in range(n_tests):
print(f"Test #{test}")
s = env.reset()
done = False
epsilon = 0
while True:
time.sleep(delay)
env.render()
a = epsilon_greedy(Q, epsilon, n_actions, s, train=True)
print(f"Chose action {a} for state {s}")
s, reward, done, info = env.step(a)
if done:
if reward > 0:
print("Reached goal!")
else:
print("Shit! dead x_x")
time.sleep(3)
break
if __name__ =="__main__":
alpha = 0.4
gamma = 0.999
epsilon = 0.1
episodes = 10000
max_steps = 2500
n_tests = 2
timestep_reward = qlearning(alpha, gamma, epsilon, episodes, max_steps, n_tests, test = True)
print(timestep_reward)
我们需要重点关注的是epsilon_greedy,sarsa和qlearning方法,我对其中对应了算法思路的部分进行了注释。可以发现,两个算法有两处区别。
区别一在于评估 s ′ s\prime s′的Value(为了评估
a_ = np.argmax(Q[s_, :])
sarsa采用的是a_ = epsilon_greedy(Q, epsilon, n_actions, s_),而如果将epsilon_greedy中的关键代码拿出来并做适当的转换,可以认为sarsa实际上采用的是:
if np.random.rand() < epsilon:
a_ = np.argmax(Q[s, :])
else:
a_ = np.random.randint(0, n_actions)
也就是说,在计算Q-Value时,qlearning永远是贪婪的(找到Q表中该stata对应最大Q-Value的a),而sarsa只有 1 − ϵ 1-\epsilon 1−ϵ的概率是贪婪的。
第二个区别在于下一个状态s_的实际采取的行动a_ 。SARSA直接使用评估 s ′ s\prime s′的Value时选择的a_,而qlearning又重新使用epsilon_greedy来决定实际采取的行动。
推荐阅读
DQN 从入门到放弃1 DQN与增强学习
DQN 从入门到放弃2 增强学习与MDP
DQN 从入门到放弃3 价值函数与Bellman方程
DQN 从入门到放弃4 动态规划与Q-Learning
DQN从入门到放弃5 深度解读DQN算法
DQN从入门到放弃6 DQN的各种改进
DQN从入门到放弃7 连续控制DQN算法-NAF
DQN实战篇1 从零开始安装Ubuntu, Cuda, Cudnn, Tensorflow, OpenAI Gym
深度增强学习之Policy Gradient方法1
DRL之Policy Gradient, Deterministic Policy Gradient与Actor Critic
星际争霸2人工智能研究环境SC2LE初体验