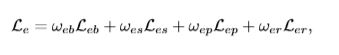暗光增强论文Attention Guided Low-light Image Enhancement with a Large Scale Low-light Simulation Dataset翻译

Abstract

低光图像增强是一个挑战，因为它不仅需要考虑亮度恢复，还需要考虑复杂的问题，如颜色失真和噪声通常隐藏在黑暗中。简单地调整低光图像的亮度将不可避免地放大这些噪声。针对这一难题，本文提出了一种基于多分支卷积神经网络的端到端注意引导方法。为此，我们首先使用精心设计的微光模拟策略构建一个合成数据集，它比现有数据集更大、更多样化。利用新的训练数据集，我们的方法学习了两个注意图，分别指导亮度增强和去噪任务。第一个注意图区分了曝光不足的区域和光线充足的区域，第二个注意图区分了噪音和真实纹理。在他们的指导下，提出的多分支分解融合增强网络以输入自适应的方式工作。此外，增强网络进一步增强输出图像的颜色和对比度。在多个数据集上的大量实验表明，我们的方法可以对低光图像产生高保真度增强结果，并且在数量和视觉上都大大超过当前的先进方法。

1 Introduction

面临的挑战

现有方法的缺陷

如何将去噪和增强过程简单地串联起来是一个难题。特别是增强前的去噪会导致模糊，而去噪前的增强会导致噪声放大。因此，在本文中，我们提出了同时建模和解决去噪和低光增强问题的方法。

我们发现，低亮度/对比度和良好图像的噪声分布都表现出与曝光不足区域分布的强相关性。因此，关键在于以区域感知的自适应方式处理问题。为此，我们建议使用曝光不足(ue)注意图来评估曝光不足的程度。这就指导了该方法在弱光增强时对欠曝光区域的重视。另外，在ue注意图的基础上，推导出噪声图，根据曝光与噪声强度的联合分布指导去噪。随后，我们设计了一个多分支CNN，在两幅图的指导下，同时实现低光增强和去噪。在最后一步，我们添加了一个全卷积网络，作为第二次增强来改善图像的对比度、曝光和颜色。

剩下的困难在于缺乏大规模的配对低光图像数据集，使得训练一个有效的网络具有挑战性。为了解决这一问题，我们提出了一种低光图像仿真管道来合成具有良好曝光的地面真实图像的低光图像。图像对比度和颜色也得到了改善，为我们的图像再增强步骤提供了良好的参考。基于上述思路，我们提出了一个大规模的低光图像数据集作为低光增强研究的有效基准。

总的来说，我们的贡献有三方面:

1)我们提出了一个完整的高保真的低光图像仿真管道，在此基础上，我们建立了一个新的大规模的配对低光图像数据集，以支持低光增强研究。

2)提出了一种注意引导增强方法和相应的多分支网络结构。该方法在ue注意图和噪声图的指导下，同时实现了低光增强和去噪。

3)进行了综合实验，实验结果表明，我们的方法大大优于目前最先进的方法。

2 Related Work

3 Large Scale Low-Light Simulation Dataset

在本文中，我们提出了一种有效的低光模拟方法来从正常光图像中合成低光图像。目的是提供一个大的多样性的场景和光照条件的数据集，这是我们的方法和其他进一步的研究所需要的。很多之前的工作[29,64]已经证明，在不同的视觉任务中，合成数据是真实数据的有效替代。使用合成数据可以使模型更容易地适应目标条件，而不需要额外的手工注释[17,63]。同样，我们认为从公共数据集[6,21,26,49]生成具有丰富注释的合成微光图像数据集也有潜力在微光条件下实现模型自适应。建议的数据集构建管道如图2所示。

3.1 Candidate Image Selection

介绍了图像选择标准

3.2 Target Image Synthesis

低光图像生成方法

我们数据集中的高质量图像可以作为低光增强的参考。但是，直接使用它们训练图像到图像的回归方法可能会导致低对比度的结果(参见图10中的MBLLEN[51]结果)。造成低对比度的可能原因可能是所选图像存在轻度过曝，这将指导增强算法倾向于产生轻度过曝的结果。此外，去除噪声所带来的平滑性也会导致低对比度。

为了克服这一限制，我们提出了一种对比度放大方法，通过合成一组新的高质量图像作为第二步增强的基础。特别地，我们应用曝光融合来改善对比度/颜色和校正曝光。首先，我们使用gamma变换从每张原始图像合成10张具有不同曝光设置和饱和度的图像。随后，我们按照[53]中的相同方法融合这些不同的公开图像(结果称为彩色图像)。最后，我们应用图像平滑[79]进一步增强图像细节。最终输出的图像称为高对比度图像，可以用作地面真实训练视觉更好的低光增强网络。

3.3 Comparison of Low-light Enhancement Datasets

总之，我们的合成数据集比现有数据集有很多优点。我们的合成数据集包含高质量的成对像素对齐图像与各种场景，不同的照明条件，以及不同的欠曝光水平。此外，这种模拟可以应用于带有注释的数据集，这对于在低光照条件下的模型适应是很有用的。我们的合成数据集是现有低光增强数据集的重要补充。

4 Attention-guided Low-light Enhancement

在这一节中，我们介绍了提出的注意力引导增强解决方案，包括网络架构、丢失功能和实现细节。

4.1 Network Architecture

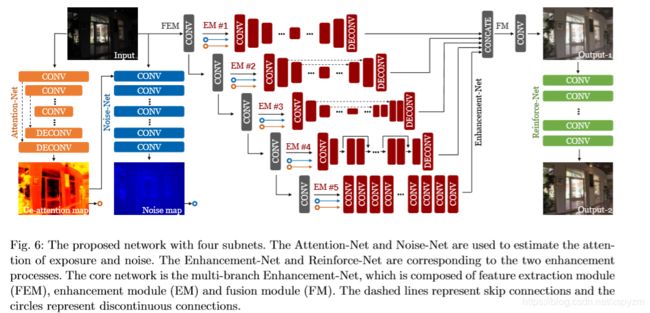
我们提出一个包含四个子网的全卷积网络:一个注意网、一个噪声网、一个增强网和一个强化网。图6显示了整个网络体系结构。设计了用于估计光照的注意网，以指导该方法在增强过程中更多地关注曝光不足的区域。同样地，噪声网被设计用来指导去噪过程。在他们的指导下，多分支增强网络可以同时进行增强和去噪。强化网是为了再次增强对比度而设计的，以解决由回归引起的低对比度限制。具体描述如下。

Attention-Net

我们在实施过程中直接采用了U-Net。其目的是为了指导增强网络正确地增强未充分暴露的区域，避免过度增强正常暴露的区域。输出是一个ue-attention图，来显示区域曝光不足水平，如图7所示。光照越高，ue-attention图值越低。ue-attention图的值范围为[0,1]，由下式计算:

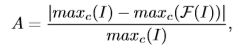
其中maxc(x)返回三个颜色通道之间的最大值，I为原来亮度的图像，F(I)为欠曝光图像的合成图像。

如图7所示，倒置的ui -attention映射看起来有点类似于Retinex模型的照明映射。由此推断，我们的用户注意图包含了流行的retinex模型所使用的重要信息。另一方面，在Retinex模型中使用我们的反向ue-attention图仍然不能保证令人满意的结果。这是因为基于retinex的解决方案在处理黑色区域时会遇到困难(参见图1中的黑色区域)，并且会导致噪声放大(参见图11中的LIME结果)。因此，我们建议使用ue -attention map作为我们稍后介绍的增强网络的指导。

Noise-Net

图像噪声很容易与图像纹理混淆，应用简单的去噪方法后会造成不必要的模糊效果。预先估计噪声分布，并自适应去噪可以减少这种影响。噪声由下式映射到取值范围为[0,1]：

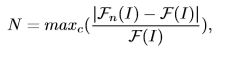
其中maxc(x)返回三个颜色通道之间的最大值，Fn(I)为合成的微光图像，F(I)为合成的欠曝光图像。

请注意，噪声分布与曝光分布高度相关，因此我们建议使用ue -attention图来帮助获得噪声图。在他们的指导下，增强网络可以有效地进行去噪。噪声网由膨胀卷积层组成，增加感受野，有利于噪声的估计。

Enhancement-Net

其动机是将增强问题分解为几个不同方面的子问题(如去噪、保留纹理、色彩校正等)，分别进行求解，通过多分支产生最终输出融合。特征提取模块(FEM)、增强模块(EM)和融合模块(FM)是该网络的核心组件。FEM是一个具有多个卷积层的单分支网络，每个卷积层使用3×3个内核、1的stride和ReLU非线性。每一层的输出既是下一层的输入，也是EM相应子网的输入。EMs是FEM各卷积层下的模块。EM的输入是FEM中某一层的输出，输出大小与输入相同。FM接受所有EMs的输出以生成最终的增强图像。我们将EMs的所有输出连接到颜色通道中，并使用1×1卷积核将其合并，等于加权求和，权重可学。（这里增强网络的设计似乎有点特征金字塔的感觉，是想把浅层细节信息和深层语义信息结合起来进行去噪）

我们提出了5种EM结构，如图六所示，EM的设计基于UNet和resNet，这被证明是有效的。简而言之，EM-1是具有较大内核大小的卷积和反卷积层的堆栈。EM-2和EM-3具有U-Net一样的结构，不同之处在于跳跃连接的实现和特征映射的大小。EM-4具有类似于Res-Net的结构。我们删除了批处理规范化[39]，并仅使用几个res块来减少模型参数。EM-5由空洞卷积层组成，其输出大小与输入大小相同。

Reinforce-Net

其动机是克服低对比度缺点并改进细节(参见图10中MBLLEN[51]与我们的区别)。之前的研究[12]证明了膨胀卷积在图像处理中的有效性。因此，我们使用类似的网络来同时提高对比度和细节。

4.2 Loss Function

为了从定性和定量两方面提高图像质量，进一步考虑图像的结构信息、感知信息和区域差异，提出了一种新的损失函数。它表示为:

分别表示四个网络的损失，细节见下文

Attention-Net loss

为了获得正确的用户注意图来指导增强网络，我们使用L2误差度量来测量预测误差:

Noise-Net los

同样地，我们使用L1误差度量来测量噪声网络的预测误差:

Enhancement-Net loss

由于图像亮度较低，仅使用mse或mae等常见误差指标可能会导致结构失真，如模糊效果和伪影。我们设计了一个新的损失，包括四个组成部分，以提高视觉质量。定义为:

分别代表亮度损失，结构损失，感知损失和局部损失

亮度损失是为了确保增强后的结果有足够的亮度而设计的。定义为:

引入结构损失来保持图像结构，避免图像模糊。我们使用著名的图像质量评估算法SSIM[76]来构建我们的结构损失。结构损失定义为:

引入感知损失，利用高级信息来提高视觉质量。我们使用表现良好的VGG网络[69]作为上下文提取器[45]。特别地，我们根据预先训练的VGG-19网络的ReLU激活层的输出来定义感知损失。知觉损失的定义如下:

对于弱光图像的增强，除了要将图像作为一个整体进行处理外，还应多注意曝光不足的区域。我们提出了局部损失来平衡不同区域的增强程度。定义为:

Reinforce-Net loss

与增强网络损失相似，定义强化网络损失为:

4.3 Implementation Details

我们的实现是用Keras[15]和Tensorflow[1]完成的。使用所提出的数据集，在Titan- x GPU上进行20个epoch的训练后，所提出的网络可以快速收敛。为了防止过拟合，我们使用随机裁剪、翻转和旋转来增加数据。我们将批量大小设置为8，随机裁剪patch的大小设置为256×256×3。输入的图像值被缩放到[0,1]。我们使用VGG-19网络第三块的第四个卷积层的输出作为感知损失的提取层。

在实验中,训练是通过使用Adam优化器[42]参数α= 0.0002,β1 = 0.9,β2 = 0.999, e= 10−8。我们还使用了学习率衰减策略，使学习率在下一个epoch之前降低到98%。同时，当损失停止改进时，我们将学习率降低到50%。

5 Experimental Evaluation