GCN&GAT 数据加载代码整理

本文是针对论文源代码数据加载部分自己的理解及整理，本人用的是Tensorflow2.0环境，数据集用的是Cora数据集。

import numpy as np
import pickle as pkl
import networkx as nx
import scipy.sparse as sp
from scipy.sparse.linalg.eigen.arpack import eigsh
import sys

这是用到的包的导入，如果运行显示NotFound直接pip安装一下即可。

def load_data(dataset_str):
  
    names = ['x', 'y', 'tx', 'ty', 'allx', 'ally', 'graph']
    objects = []
    for i in range(len(names)):
        with open("data/ind.{}.{}".format(dataset_str, names[i]), 'rb') as f:
            if sys.version_info > (3, 0):
                data = pkl.load(f, encoding='latin1')
                if(names[i].find('graph')==-1):
                     for j in range(data.shape[0]):
                        print('********',names[i],j,data[j].shape,'**********')
                        print(data[j])
                else:
                    print(f)
                    print(data)
                objects.append(data)

            else:
                objects.append(pkl.load(f))

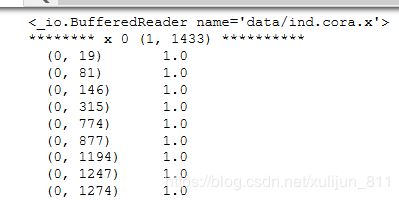
    x, y, tx, ty, allx, ally, graph = tuple(objects)

Cora数据集是包含1433个独特单词，所以他的特征是1433维的，其中x是训练数据的特征向量，shape(140 1433)，有140个节点，1433是特征向量的维数；y是训练数据的标签，shape(140,7)，7是指7类，cora数据集是分为了七大类；tx是测试数据的特征向量，shape(1000 1433)，有1000个测试实例；ty是测试数据的标签，shape(1000 7),allx是训练集中所有训练实例是从0到1707共1708个，shape(1708 1433);allly是allx对应的标签，是从1708到2707共1000个，shape是（1708 7）；graph是图数据，共有节点2708个。代码中的data是可以输出矩阵中非0的行列坐标及值，最后把他们转换成元组的形式。打印部分结果如图：

这是x第0行的非零的行列坐标及值，我理解的1是这个位置有值。

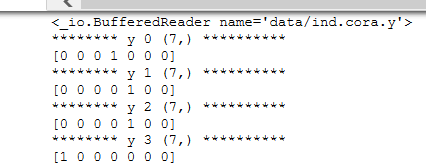
这是y第0 1 2 3   ....行的值，0和1是对应标签的标记。只是部分截图，其余可自己打印，我觉得打印后会对数据集理解更深刻。

##graph是一个字典，大图总共2708个节点
    print("图节点")
    for i in graph:
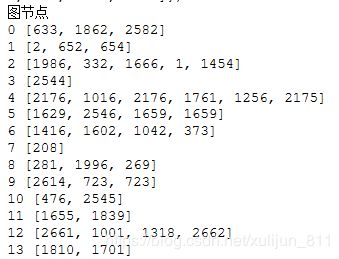
        print(i,graph[i])

输出图节点，运行如下，部分截图。

可以清楚的看到每个节点的位置，0是与633，1862，2582这三个节点相连接的，以此类推。

def parse_index_file(filename):
    """Parse index file."""
    index = []
    for line in open(filename):
        index.append(int(line.strip()))
        #print(int(line.strip()))
    print("min", min(index))
    return index

#索引乱序
    test_idx_reorder = parse_index_file("data/ind.{}.test.index".format(dataset_str))
     # print(test_idx_reorder)
    # [2488, 2644, 3261, 2804, 3176, 2432, 3310, 2410, 2812,...]
    
    #从小到大排序
    test_idx_range = np.sort(test_idx_reorder)
    print("输出索引")
    print(test_idx_range)

以上两部分是按行读取test.index这个文件进行索引，然后从小到大排序，最小是1708，也就是从1708到2707。运行结果如下 ，部分截图。

 if dataset_str == 'citeseer':#处理citeseer中一些孤立的点
        # Fix citeseer dataset (there are some isolated nodes in the graph)
        # Find isolated nodes, add them as zero-vecs into the right position
        test_idx_range_full = range(min(test_idx_reorder), max(test_idx_reorder)+1)
        #print("*******")
        #print("test_idx_range_full.length",len(test_idx_range_full))
        # test_idx_range_full.length 1015
        tx_extended = sp.lil_matrix((len(test_idx_range_full), x.shape[1]))
        #print(tx_extended)
        # test_idx_range-min(test_idx_range):列表中每个元素都减去min(test_idx_range)，即将test_idx_range列表中的index值变为从0开始编号
        tx_extended[test_idx_range-min(test_idx_range), :] = tx
        #print(tx_extended.shape) #(1015, 3703)
        tx = tx_extended 
        # print(tx.shape)
        # (1015, 3703)
        # 997,994,993,980,938...等15行全为0
        ty_extended = np.zeros((len(test_idx_range_full), y.shape[1]))#zero返回来一个给定形状和类型的用0填充的数组；
        ty_extended[test_idx_range-min(test_idx_range), :] = ty
        ty = ty_extended
         # for i in range(ty.shape[0]):
        #     print(i," ",ty[i])
        #     # 980 [0. 0. 0. 0. 0. 0.]
        #     # 994 [0. 0. 0. 0. 0. 0.]
        #     # 993 [0. 0. 0. 0. 0. 0.]

每个数据集都会出现一些脱离模型的点也叫孤立点，这个处理孤立点的方式是找到test.index中没有对应的索引，一共有15个，把这些点当作特征全为0的节点加入到测试集中，并且对应的标签在ty中。

# 将allx和tx叠起来并转化成LIL格式的feature,即输入一张整图
    features = sp.vstack((allx, tx)).tolil()#vstact:将数组堆叠成一列
    #print(features.shape)
    features[test_idx_reorder, :] = features[test_idx_range, :]
    # 邻接矩阵格式也是LIL的，并且shape为(2708, 2708)
    adj = nx.adjacency_matrix(nx.from_dict_of_lists(graph))#from_dict_of_lists图转换为字典
    print(adj,adj.shape)
 # labels.shape:(2708, 7)
    labels = np.vstack((ally, ty))
    #print(labels.shape)
    labels[test_idx_reorder, :] = labels[test_idx_range, :]
    #print(labels[test_idx_reorder, :])
# len(list(idx_val)) + len(list(idx_train)) + len(idx_test) =  1640
    idx_test = test_idx_range.tolist()
    # print(idx_test)
    # [1708, 1709, 1710, 1711, 1712, 1713,...,2705, 2706, 2707]
    # print(len(idx_test))
    # 1000
    idx_train = range(len(y))
    # print(idx_train)
    # range(0, 140)
    idx_val = range(len(y), len(y)+500)
    # print(idx_val,len(idx_val))
    # range(140, 640) 500

这部分是将allx和tx按列进行堆叠变成了features shape是（2708 1433）。labels是将ally和ty按列堆叠，shape是（2708，7），这里面的from_dict_of_lists()函数是将图转换为字典的形式，这里面的稀疏矩阵都是按LIL格式存储的，lil_matrix则是使用两个列表存储非0元素。data保存每行中的非零元素,rows保存非零元素所在的列。这种格式也很适合逐个添加元素，并且能快速获取行相关的数据。关于稀疏矩阵的存储有很多种方式各有优缺点，可参考这篇https://www.cnblogs.com/zhangchaoyang/articles/5483453.html。features[test_idx_reorder, :] = features[test_idx_range, :]这个代码是为了还原特征向量和邻接矩阵对齐，可是他是怎么对齐的 什么原理暂时还没搞懂。

下图是邻接矩阵打印部分结果，邻接矩阵shape是（2708 2708）

    # 训练mask：idx_train=[0,140)范围的是True，后面的是False
    train_mask = sample_mask(idx_train, labels.shape[0])
    # print(train_mask,train_mask.shape)
    # [True  True  True... False False False]  # labels.shape[0]:(2708,)
    
    # 验证mask：val_mask的idx_val=(140, 640]范围为True，其余的是False
    val_mask = sample_mask(idx_val, labels.shape[0])
    # test_mask，idx_test=[1708,2707]范围是True，其余的是False
    test_mask = sample_mask(idx_test, labels.shape[0])

    y_train = np.zeros(labels.shape)
    y_val = np.zeros(labels.shape)
    y_test = np.zeros(labels.shape)
     #print(y_train.shape," ",y_test.shape," ",y_val.shape)
    # (2708, 7)(2708, 7)(2708, 7)
    
    # 替换了true位置
    y_train[train_mask, :] = labels[train_mask, :]
    y_val[val_mask, :] = labels[val_mask, :]
    y_test[test_mask, :] = labels[test_mask, :]    
    return adj, features, y_train, y_val, y_test, train_mask, val_mask, test_mask

load_data('cora')

最后是创建mask掩码，mask是包含0和1的矩阵，用zero返回来一个给定形状和类型的用0填充的数组形成三个shape（2708 7）的0矩阵，然后把true的地方替换成1，mask掩码这部分是找到对数据有影响的部分标记为1，没有影响的部分为0直接掩盖掉。

虽然只是数据加载这一部分，我理解的仍然不是很好，如果想要在图神经和图注意这块学好，真的要结合代码运行出结果举出小例子亲自算一算才会理解更加深刻，源代码正在看，会继续更新笔记，欢迎各位大佬指正批评。