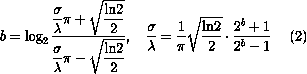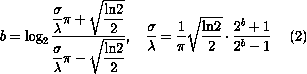Gabor滤波器学习（代码调试）

说明：介绍Gabor滤波器的基本形式，不涉及Gabor滤波器组的设计。

参考资料：

1 http://matlabserver.cs.rug.nl/edgedetectionweb/web/edgedetection_params.html

2 http://www.cs.rug.nl/~imaging/simplecell.html

一 引言

二维Gabor滤波器是一个高斯函数和一个复数波的相乘。其中，二维复数波的实部图像表现为条纹状图像，如正弦波一样，因此在某些文献中又将复数波称为复数正弦波。

Gabor滤波器的实部由下面的公式给定（见参考资料1）：

另外，高斯函数的参数sigma由参数lamda和b确定（见参考资料1及程序代码）：

为了更好地理解二维Gabor滤波器，我们用MATLAB分别绘制不同参数下复数波、高斯函数的图像形式，并在此基础上绘制二维Gabor滤波器的图像形式。

内容包括三个层面：

1 复数波实部图像（参数）

2 高斯函数图像（参数）

3 Gabor滤波器（参数）

二 复数波实部图像及其参数

1 MATLAB代码调试

% 调试复数波的实部图像
% 公式：
%         x1 = x*cos(theta) + y*sin(theta);
%         Fushubo_real = cos(2*pi*x1/lamda + phi); 
% 参数：
% % x,y   : 坐标
% % theta : 复数波中明暗条纹的垂线方向与x轴的夹角（specifies the orientation of the normal to the parallel stripes of the Gabor function.）；单位度（实际程序中，再转化为弧度）
%             This parameter specifies the orientation of the normal to the parallel stripes of 
%             a Gabor function. Its value is specified in degrees. Valid values are real numbers 
%             between 0 and 360.
% % lamda : 复数波的波长（specifies the wavelength of the cosine factor of the Gabor function.）
%             This is the wavelength of the cosine factor of the Gabor filter kernel and herewith 
%             the preferred wavelength of this filter. Its value is specified in pixels. Valid 
%             values are real numbers equal to or greater than 2. The value λ=2 should not be 
%             used in combination with phase offset φ=-90 or φ=90 because in these cases the 
%             Gabor function is sampled in its zero crossings. In order to prevent the occurence 
%             of undesired effects at the image borders, the wavelength value should be smaller 
%             than one fifth of the input image size.
% % phi   : 设置初始相位（specifies the phase offset of the cosine factor of the Gabor function）
%             The phase offset φ in the argument of the cosine factor of the Gabor function is 
%             specified in degrees. Valid values are real numbers between -180 and 180. The values 
%             0 and 180 correspond to center-symmetric 'center-on' and 'center-off' functions, 
%             respectively, while -90 and 90 correspond to anti-symmetric functions. All other 
%             cases correspond to asymmetric functions.
clear
close all
theta = 0; theta = theta * pi / 180;%转化为弧度
lamda = 15;%5,10,15
phi = 180;

zl_h = 100;
zl_w = 100;
Img = zeros(2*zl_h+1,2*zl_w+1);

Pianzhi = zl_h+1;
for zl_i = -zl_h:1:zl_h %纵坐标
    for zl_j =-zl_w:1:zl_w %横坐标
%         x1 = zl_i*cos(theta) + zl_j*sin(theta);
        x1 = zl_j*cos(theta) + zl_i*sin(theta);%前者是横坐标，后者是纵坐标，顺序不能颠倒。
        Img(zl_i+Pianzhi,zl_j+Pianzhi) = cos(2*pi*x1/lamda + phi);            
    end
end

figure
imshow(Img,[])
Img_fft = fftshift(fft2(Img));
fft_abs = abs(Img_fft);
figure,imshow(fft_abs,[])
% imtool(fft_abs,[])

2 参数调试

2.1 Theta = 0°,45°,90°（在程序中，转化为弧度）

其他参数：lamda(wavelength)=10, phi(phase offset)=0.

备注：% % theta : 明暗条纹的垂线方向与x轴的(顺时针)夹角（specifies the orientation of the normal to the parallel stripes of the Gabor function.）；单位度（实际程序中，再转化为弧度）

%             This parameter specifies the orientation of the normal to the parallel stripes of

%             a Gabor function. Its value is specified in degrees. Valid values are real numbers

%             between 0 and 360.

小结：1从实验结果（第一行）可知，明暗条纹的垂线方向与x轴的(顺时针)夹角分别为0°，45°，90°，与实验预期相同。2计算各“正弦波图像”的幅度谱，如第二行所示，可见两频点所在直线方向与明暗条纹的垂线方向相同。

2.2 lamda(wavelength)=5,10,15

其他参数：Theta (orientation)=0, phi(phase offset)=0.

备注：% % lamda : 复数波的波长（specifies the wavelength of the cosine factor of the Gabor function.）

%             This is the wavelength of the cosine factor of the Gabor filter kernel and herewith

%             the preferred wavelength of this filter. Its value is specified in pixels. Valid

%             values are real numbers equal to or greater than 2. The value λ=2 should not be

%             used in combination with phase offset φ=-90 or φ=90 because in these cases the

%             Gabor function is sampled in its zero crossings. In order to prevent the occurence

%             of undesired effects at image borders, the wavelength value should be smaller

%             than one fifth of the input image size.

小结：从实验结果可以看出，随着波长的增加，正弦波图像的条纹间隔增大，而相应的幅度谱中频率逐渐减小（向中心处的低频分量靠近）；可见，波长lamda(wavelength)与图像的“空间频率（1 / lambda the spatial frequency）”呈反比。

2.3 phi(phase offset)=  0°, 180°, -90° and 90°

其他参数：Theta (orientation)=0, lamda(wavelength)=15

备注：% % phi   : 设置初始相位（specifies the phase offset of the cosine factor of the Gabor function）

%             The phase offset φ in the argument of the cosine factor of the Gabor function is

%             specified in degrees. Valid values are real numbers between -180 and 180. The values

%             0 and 180 correspond to center-symmetric 'center-on' and 'center-off' functions,

%             respectively, while -90 and 90 correspond to anti-symmetric functions. All other

%             cases correspond to asymmetric functions. 解析：初始相位用于控制Gabor滤波器的对称性（奇对称、偶对称、不对称）

小结：从实验结果可以看出，随着初始相位的变化，正弦波条纹发生了沿法线方向产生了平移现象。另外，从实验结果可以看出，随着初始相位的变化，频域幅度谱并未发生变化，即相位变化并不影响图像的幅度谱。

 

三 高斯函数图像及其参数

3.1 代码调试

% 调试高斯函数的图像
% 公式：
%         x1 = x*cos(theta) + y*sin(theta);
%         y1 = -x*sin(theta) + y*cos(theta);
%         gaussi = exp(-((x1^2 + gamma^2 * y1^2)/(2*(sigma^2))));
%         sigma  = lamda * (1/pi) * sqrt((log(2))/2) * (2^b + 1)/(2^b -1);
% 参数：
% % x,y   : 坐标
% % theta(Orientation(s)) : 复数波中明暗条纹的垂线方向与x轴的夹角（specifies the orientation of the normal to the parallel stripes of the Gabor function.）；单位度（实际程序中，再转化为弧度）
%             This parameter specifies the orientation of the normal to the parallel stripes of 
%             a Gabor function. Its value is specified in degrees. Valid values are real numbers 
%             between 0 and 360.
% % sigma :
%             Sigma is The standard deviation of the Gaussian factor determines the (linear) size
%             of the receptive field. Sigma cannot be controlled directly in the applet. Its 
%             value is determined by the choice of the parameters lambda and b.
% % gamma(Aspect ratio,γ) :            
%             gamma, called the spatial aspect ratio, specifies the ellipticity 
%             of the support of the Gabor function. For γ = 1, the support is circular. 
%             For γ < 1 the support is elongated in orientation of the parallel 
%             stripes of the function. Default value is γ = 0.5.It has been 
%             found to vary in a limited range of 0.23 < gamma < 0.92. 
% % lamda(Wavelength,λ) : 复数波的波长（specifies the wavelength of the cosine factor of the Gabor function.）
%             This is the wavelength of the cosine factor of the Gabor filter kernel and herewith 
%             the preferred wavelength of this filter. Its value is specified in pixels. Valid 
%             values are real numbers equal to or greater than 2. The value λ=2 should not be 
%             used in combination with phase offset φ=-90 or φ=90 because in these cases the 
%             Gabor function is sampled in its zero crossings. In order to prevent the occurence 
%             of undesired effects at the image borders, the wavelength value should be smaller 
%             than one fifth of the input image size.
% % b(Bandwidth) :
%             The half-response spatial frequency bandwidth b (in octaves) of a Gabor filter 
%             is related to the ratio σ / λ, where σ and λ are the standard deviation 
%             of the Gaussian factor of the Gabor function and the
%             preferred wavelength, respectively, as follows:
%            σ / λ = (1/pi) * sqrt((log(2))/2) * (2^b + 1)/(2^b -1)

clear
close all
theta = 0; theta = theta * pi / 180;%转化为弧度
b = 2;
lamda = 10; sigma = lamda * (1/pi) * sqrt((log(2))/2) * (2^b + 1)/(2^b -1);
gamma = 0.5;
phi = 0;

zl_h = 100;
zl_w = 100;
Img = zeros(2*zl_h+1,2*zl_w+1);

Pianzhi = zl_h+1;
for zl_i = -zl_h:1:zl_h %纵坐标
    for zl_j =-zl_w:1:zl_w %横坐标
        x1 = zl_j*cos(theta) + zl_i*sin(theta);%前者是横坐标，后者是纵坐标，顺序不能颠倒。
        y1 = -zl_j*sin(theta) + zl_i*cos(theta);
        Img(zl_i+Pianzhi,zl_j+Pianzhi) = exp(-((x1^2 + gamma^2 * y1^2)/(2*(sigma^2))));
        
    end
end

figure
imshow(Img,[])
Img_fft = fftshift(fft2(Img));
fft_abs = abs(Img_fft);
figure,imshow(fft_abs,[])

3.2 lamda(Wavelength,λ) =5, 10 and 15

其他参数：orientation 0, aspect ratio 0.5, and bandwidth 1.

小结：已知空间域图像中高斯图像的覆盖区域有参数sigma控制，而在实际使用中sigma并非直接给定，它由复平面正弦波的波长（即the wavelength of the cosine factor of the Gabor filter kernel）和The half-response spatial frequency bandwidth b来确定。由实验测试结果可知，当给定bandwidth恒为1时，sigma随着wavelength的增大而增大，表现为高斯图像的覆盖区域逐渐增大。

另外，由实验测试结果可知，高斯图像的频域幅度谱仍然是高斯型图像，并且随着高斯图像覆盖区域的逐渐扩大，相应的频域幅度谱中高斯图像覆盖范围逐渐缩小。

3.3Orientation(s) (θ)=  0, 45 and 90

其他参数：wavelength 10, phase offset 0, aspect ratio 0.5, and bandwidth 1

小结：可见，当θ=0时，长轴的法向与x轴呈0度，当θ为45度时，长轴的法向与x轴呈-45度，即顺时针旋转了45度。

3.4 Aspect ratio (γ) = 0.3 0.5 1

其他参数：wavelength 10, orientation 0, phase offset 0, and bandwidth 1.

小结：可见gamma用来控制高斯覆盖区域（椭圆形）的长短轴比例，且短/长 = gamma。

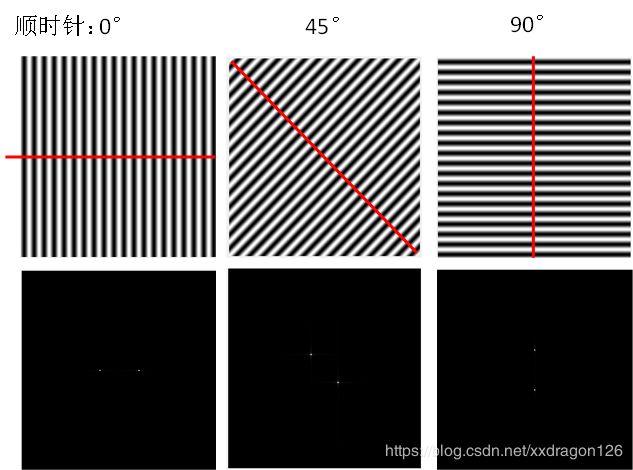
3.5 Bandwidth (b) =0.5, 1, and 2

其他参数：wavelength 10, orientation 0, phase offset 0, and aspect ratio 0.5

小结：已知空间域图像中高斯图像的覆盖区域有参数sigma控制，而在实际使用中sigma并非直接给定，它由复平面正弦波的波长（即the wavelength of the cosine factor of the Gabor filter kernel）和The half-response spatial frequency bandwidth b来确定。由实验测试结果可知，当给定wavelength恒为10时，sigma随着bandwidth b的增大而减小，表现为高斯图像的覆盖区域逐渐缩小。

四 Gabor滤波器及其参数

4.1 代码调试

% 调试Gabor滤波器的实部图像
% 公式：
%         x1 = x*cos(theta) + y*sin(theta);
%         y1 = -x*sin(theta) + y*cos(theta);
%         gaussi = exp(-((x1^2 + gamma^2 * y1^2)/(2*(sigma^2))));
%         sigma  = lamda * (1/pi) * sqrt((log(2))/2) * (2^b + 1)/(2^b -1);
%         Fushubo = exp(1i* (2*pi*x1/lamda + phi))
%         Fushubo_real = cos(2*pi*x1/lamda + phi); 
%         Gabor = gaussi * Fushubo;
%         Gabor_real = gaussi * Fushubo_real;
% 参数：
% % x,y   : 坐标
% % theta(Orientation(s)) : 复数波中明暗条纹的垂线方向与x轴的夹角（specifies the orientation of the normal to the parallel stripes of the Gabor function.）；单位度（实际程序中，再转化为弧度）
%             This parameter specifies the orientation of the normal to the parallel stripes of 
%             a Gabor function. Its value is specified in degrees. Valid values are real numbers 
%             between 0 and 360.
% % sigma :
%             Sigma is The standard deviation of the Gaussian factor determines the (linear) size
%             of the receptive field. Sigma cannot be controlled directly in the applet. Its 
%             value is determined by the choice of the parameters lambda and b.
% % gamma(Aspect ratio,γ) :            
%             gamma, called the spatial aspect ratio, specifies the ellipticity 
%             of the support of the Gabor function. For γ = 1, the support is circular. 
%             For γ < 1 the support is elongated in orientation of the parallel 
%             stripes of the function. Default value is γ = 0.5.It has been 
%             found to vary in a limited range of 0.23 < gamma < 0.92. 
% % lamda(Wavelength,λ) : 复数波的波长（specifies the wavelength of the cosine factor of the Gabor function.）
%             This is the wavelength of the cosine factor of the Gabor filter kernel and herewith 
%             the preferred wavelength of this filter. Its value is specified in pixels. Valid 
%             values are real numbers equal to or greater than 2. The value λ=2 should not be 
%             used in combination with phase offset φ=-90 or φ=90 because in these cases the 
%             Gabor function is sampled in its zero crossings. In order to prevent the occurence 
%             of undesired effects at the image borders, the wavelength value should be smaller 
%             than one fifth of the input image size.
% % b(Bandwidth) :
%             The half-response spatial frequency bandwidth b (in octaves) of a Gabor filter 
%             is related to the ratio σ / λ, where σ and λ are the standard deviation 
%             of the Gaussian factor of the Gabor function and the
%             preferred wavelength, respectively, as follows:
%            σ / λ = (1/pi) * sqrt((log(2))/2) * (2^b + 1)/(2^b -1)
% % phi   : 设置初始相位（specifies the phase offset of the cosine factor of the Gabor function）
%             The phase offset φ in the argument of the cosine factor of the Gabor function is 
%             specified in degrees. Valid values are real numbers between -180 and 180. The values 
%             0 and 180 correspond to center-symmetric 'center-on' and 'center-off' functions, 
%             respectively, while -90 and 90 correspond to anti-symmetric functions. All other 
%             cases correspond to asymmetric functions.

clear
close all
theta = 0; theta = theta * pi / 180;%转化为弧度
b = 2;
lamda = 10; sigma = lamda * (1/pi) * sqrt((log(2))/2) * (2^b + 1)/(2^b -1);
gamma = 0.5;
phi = 0;

zl_h = 100;
zl_w = 100;
Img = zeros(2*zl_h+1,2*zl_w+1);

Pianzhi = zl_h+1;
for zl_i = -zl_h:1:zl_h %纵坐标
    for zl_j =-zl_w:1:zl_w %横坐标
        x1 = zl_j*cos(theta) + zl_i*sin(theta);%前者是横坐标，后者是纵坐标，顺序不能颠倒。
        y1 = -zl_j*sin(theta) + zl_i*cos(theta);
        gaussi = exp(-((x1^2 + gamma^2 * y1^2)/(2*(sigma^2))));
%         Fushubo = exp(1i* (2*pi*x1/lamda + phi));
%         Img(zl_i+Pianzhi,zl_j+Pianzhi) = real(gaussi * Fushubo);%这里只取Gabor的实部
        Fushubo_real = cos(2*pi*x1/lamda + phi);
        Img(zl_i+Pianzhi,zl_j+Pianzhi) = gaussi * Fushubo_real;%这里只取Gabor的实部
        
    end
end

figure
imshow(Img,[])
Img_fft = fftshift(fft2(Img));
fft_abs = abs(Img_fft);
figure,imshow(fft_abs,[])

4.2 lamda(Wavelength,λ) =5, 10 and 15

其他参数：orientation 0, phase offset 0, aspect ratio 0.5, and bandwidth 1.

小结：已知空间域图像中高斯图像的覆盖区域有参数sigma控制，而在实际使用中sigma并非直接给定，它由复平面正弦波的波长（即the wavelength of the cosine factor of the Gabor filter kernel）和The half-response spatial frequency bandwidth b来确定。由实验测试结果可知，当给定bandwidth恒为1时，sigma随着wavelength的增大而增大，表现为高斯图像的覆盖区域逐渐增大。

另外：随着波长的增加，正弦波图像的条纹间隔增大，而相应的幅度谱中频率逐渐减小（向中心处的低频分量靠近）；可见，波长lamda(wavelength)与图像的“空间频率（1 / lambda the spatial frequency）”呈反比。

4.3Orientation(s) (θ)=  0, 45 and 90

其他参数：wavelength 10, phase offset 0, aspect ratio 0.5, and bandwidth 1.

小结：This parameter specifies the orientation of the normal to the parallel stripes of a Gabor function. 可见，当θ=0时，长轴的法向与x轴呈0度，当θ为45度时，长轴的法向与x轴呈-45度，即顺时针旋转了45度。

4.4 Phase offset(s) (φ)= 0°, 180°, -90° and 90°

其他参数：wavelength 10, orientation 0, aspect ratio 0.5, and bandwidth 1.

小结：相位变化影响Gabor滤波器中条纹的对称性。从实验结果可以看出，随着初始相位的变化，正弦波条纹发生了沿法线方向产生了平移现象。另外，从实验结果可以看出，随着初始相位的变化，频域幅度谱并未发生变化，即相位变化并不影响图像的幅度谱。

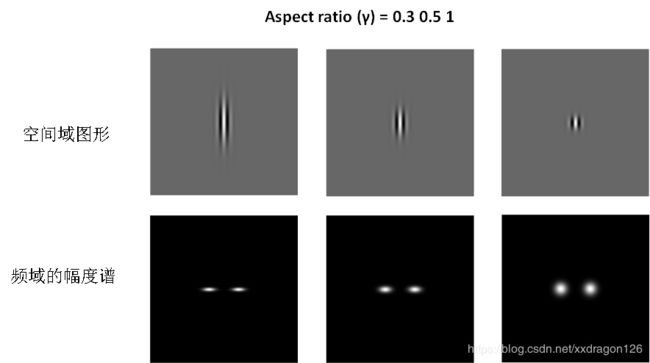
4.5 Aspect ratio (γ) = 0.3 0.5 1

其他参数：wavelength 10, orientation 0, phase offset 0, and bandwidth 1.

小结：This parameter, called more precisely the spatial aspect ratio, specifies the ellipticity of the support of the Gabor function. 即gamma用来控制高斯覆盖区域（椭圆形）的长短轴比例，且短/长 = gamma。

4.6 Bandwidth (b) =0.5, 1, and 2

其他参数：wavelength 10, orientation 0, phase offset 0, and aspect ratio 0.5

小结：已知空间域图像中高斯图像的覆盖区域有参数sigma控制，而在实际使用中sigma并非直接给定，它由复平面正弦波的波长（即the wavelength of the cosine factor of the Gabor filter kernel）和The half-response spatial frequency bandwidth b来确定。由实验测试结果可知，当给定wavelength恒为10时，sigma随着bandwidth b的增大而减小，表现为高斯图像的覆盖区域逐渐缩小。

五 补充

5.1Bandwidth (b)和lamda(Wavelength)均影响sigma，即影响Gabor滤波器的覆盖范围，满足：

1当给定wavelength恒为10时，sigma随着bandwidth b的增大而减小，表现为高斯图像的覆盖区域逐渐缩小。

2当给定bandwidth恒为1时，sigma随着wavelength的增大而增大，表现为高斯图像的覆盖区域逐渐扩大。

5.2另外lamda(Wavelength) 影响Gabor滤波器中的条纹间隔，满足：

1随着波长的增大，Gabor滤波器的条纹间隔增大，Gabor滤波器的空间频率降低。

5.3 概念补充：

The half-response of a Gabor filter （Semi -"linear 2D Gabor filter"）:

i.e., the response R is obtained by convolution (*) of the input I with a Gabor function g, followed by half-wave rectification (|.|+).