《利用PYTHON进行数据分析》——4.1 NUMPY的NDARRAY一种多维数组对象——数组转置和轴对换——读书笔记
《利用PYTHON进行数据分析》——4.1 NUMPY的NDARRAY一种多维数组对象——数组转置和轴对换——读书笔记
- 4.1 NUMPY的NDARRAY一种多维数组对象-----数组转置和轴对换
- 总结
链接: 原文链接.
链接: Python · numpy · axis.
4.1 NUMPY的NDARRAY一种多维数组对象-----数组转置和轴对换
转置是重塑的一种特殊形式,他返回的是一个源数据的视图(不会进行任何复制的操作)
数组不仅有transpose方法,还有一个特殊的T属性:
In [126]: arr = np.arange(15).reshape((3, 5))
In [127]: arr
Out[127]:
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
In [128]: arr.T
Out[128]:
array([[ 0, 5, 10],
[ 1, 6, 11],
[ 2, 7, 12],
[ 3, 8, 13],
[ 4, 9, 14]])
对于高维数组,transpose方法,需要得到一个由轴编号组成的元组才能对这些轴进行转置
transpose 方法是数组用来转置的一种方法,尤其对于高维数组,transpose需要得到一个由轴编号组成的元组才能对这些轴进行转置。那么是怎么根据这个轴来完成转置的呢?
举个例子:
举例说明:先创建一个224的三维数组:
In [59]: arrrr=np.arange(16).reshape((2,2,4))
In [60]: arrrr
Out[60]:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
我假设这个三维数组在空间中按上图的方式排列,数组里每个数字存放在一个小立方体中
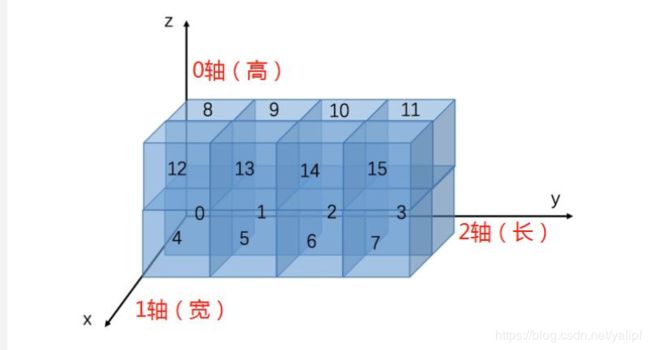
更具体一点,我们的俯视图如下:

用表格展示一下这个数据

接着装化为坐标值

这也是数组取值时使用的坐标,例如:(1,0,0)对应8
In [60]: arrrr
Out[60]:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
In [61]: arrrr[1,0,0]
Out[61]: 8
总结
三维数组的大小是2 x 2 x 4
- 最左边的为0轴=(0,1),中间的1轴=(0,1),最右边的3轴=(0,1,2,3)
- 一维数组一定要用 1 × n 来记!!
A = np.array([1, 2, 3, 4, 5, 6]) # 一维
print(A.shape)
>>>(6,) # 1X6 (1行6列)
- 整个数组一共有16个数,首先以 axis=0 为例,由于我们现在整个数组里面一共有 16个数,而axis=0 只有两个元素,就是0和1,所以可以理解为在 axis=0 这个 axis 上,每隔 16 / 2 = 8 个数就跳一下。比如说上面这个图中就可以看出,坐标(0,0,0)和坐标(1,0,0)之间差的是 8。
而axis=0考虑完以后,就考虑 axis=1,因为axis=0以8个元素为一组,而axis=0 只有两个元素,就是0和1,所以可以理解为在 axis=1 这个 axis 上,每隔 8 / 2 = 4个数就跳一下。比如说上面这个图中就可以看出,坐标(0,0,0)和坐标(0,1,0)之间差的是 4。
而axis=1考虑完以后,就考虑 axis=2,因为axis=1以4个元素为一组,而axis=2 只有4个元素,就是0,1,2,3,所以可以理解为在 axis=1 这个 axis 上,每隔 4 / 4= 1个数就跳一下。比如说上面这个图中就可以看出,坐标(0,0,0)和坐标(0,0,1)之间差的是 1。 - 最外面的括号代表0轴,中间的括号代表1轴,最里面的括号代表2轴。
In [59]: arrrr=np.arange(16).reshape((2,2,4))
In [60]: arrrr
Out[60]:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
那么接下来激动人心的时刻到了:transpose 的本质,其实就是对 strides (每隔几个数就跳一下)中各个数的顺序进行调换。举个例子:
In [59]: arrrr=np.arange(16).reshape((2,2,4))
In [60]: arrrr
Out[60]:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
In [62]: arrrr.transpose((1,0,2))
Out[62]:
array([[[ 0, 1, 2, 3],
[ 8, 9, 10, 11]],
[[ 4, 5, 6, 7],
[12, 13, 14, 15]]])
在 transpose(1, 0, 2) 后,相应的 strides 会变成 (4, 8, 1)。,原来的strides (8, 4, 1)是而从上图可以看出,transpose 的结果确实满足:
- axis=0 的 axis 上,每隔 4 个数跳一下
- axis=1 的 axis 上,每隔 8个数跳一下
- axis=2 的 axis 上,每隔 1 个数跳一下