批量梯度下降法（BGD）、随机梯度下降法（SGD）和小批量梯度下降法（MBGD）

在机器学习中，对于很多监督学习模型，需要对原始的模型构建损失函数，接下来便是通过优化算法对损失函数进行优化，以便找到最优的参数。
梯度下降法作为机器学习中较常使用的优化算法，在其求解过程中，只需要求解损失函数的一阶导数，计算的代价比较小。
基本思想可以理解为：我们从山上的某一点出发，找一个最抖的坡走一步（也就是找梯度方向），到达一个点之后，再找最陡的坡，再走一步，直到不断的走，走到最低点（最小花费函数收敛点）

梯度下降法有三种不同的形式：批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）以及小批量梯度下降（Mini-Batch Gradient Descent）。其中小批量梯度下降法也常用在深度学习中进行模型的训练。接下来，我们将对这三种不同的梯度下降法进行理解。
  为了便于理解，这里我们将使用只含有一个特征的线性回归来展开。此时线性回归的假设函数为：
  
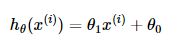
其中 i=1,2,…,m 表示样本数。
对应的目标函数（代价函数）即为：

1、批量梯度下降（Batch Gradient Descent，BGD）

批量梯度下降法是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新。从数学上理解如下：
  （1）对目标函数求偏导：
  
  其中 i=1,2,…,m 表示样本数， j=0,1 表示特征数，这里我们使用了偏置项 x(i)0=1 。
  （2）每次迭代对参数进行更新：
  
  注意这里更新时存在一个求和函数，即为对所有样本进行计算处理，可与下文SGD法进行比较。
  伪代码形式为：
  
  优点：
  （1）一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行。
  （2）由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优。
  缺点：
  （1）当样本数目 m 很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。
  从迭代的次数上来看，BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下：
  

2、随机梯度下降（Stochastic Gradient Descent，SGD）

随机梯度下降法不同于批量梯度下降，随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。
  对于一个样本的目标函数为：
  
  优点：
  （1）由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。
  缺点：
  （1）准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
  （2）可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。
  （3）不易于并行实现。

解释一下为什么SGD收敛速度比BGD要快：
  答：这里我们假设有30W个样本，对于BGD而言，每次迭代需要计算30W个样本才能对参数进行一次更新，需要求得最小值可能需要多次迭代（假设这里是10）；而对于SGD，每次更新参数只需要一个样本，因此若使用这30W个样本进行参数更新，则参数会被更新（迭代）30W次，而这期间，SGD就能保证能够收敛到一个合适的最小值上了。也就是说，在收敛时，BGD计算了 10×30W 次，而SGD只计算了 1×30W 次。

从迭代的次数上来看，SGD迭代的次数较多，在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下：

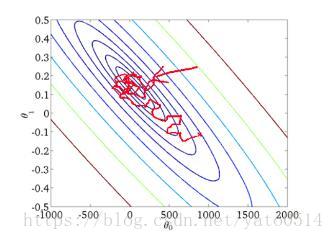
3、小批量梯度下降（Mini-Batch Gradient Descent, MBGD）

小批量梯度下降，是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是：每次迭代 使用 ** batch_size** 个样本来对参数进行更新。

优点：
  （1）通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
  （2）每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。(比如上例中的30W，设置batch_size=100时，需要迭代3000次，远小于SGD的30W次)
  （3）可实现并行化。
  缺点：
  （1）batch_size的不当选择可能会带来一些问题。

小批量的梯度下降可以利用矩阵和向量计算进行加速，还可以减少参数更新的方差，得到更稳定的收敛。在MSGD中，学习速率一般设置的比较大， 随着训练不断进行，可以动态的减小学习速率，这样可以保证一开始算法收敛速度较快。实际中如果目标函数平面是局部凹面，传统的SGD往往会在此震荡，因为一个负梯度会使其指向一个陡峭的方向，目标函数的局部最优值附近会出现这种情况，导致收敛很慢，这时候需要给梯度一个动量（momentum），使其能够跳出局部最小值，继续沿着梯度下降的方向优化，使得模型更容易收敛到全局最优值

batcha_size的选择带来的影响：
  （1）在合理地范围内，增大batch_size的好处：
    a. 内存利用率提高了，大矩阵乘法的并行化效率提高。
    b. 跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
    c. 在一定范围内，一般来说 Batch_Size 越大，其确定的下降方向越准，引起训练震荡越小。
  （2）盲目增大batch_size的坏处：
    a. 内存利用率提高了，但是内存容量可能撑不住了。
    b. 跑完一次 epoch（全数据集）所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加了，从而对参数的修正也就显得更加缓慢。
    c. Batch_Size 增大到一定程度，其确定的下降方向已经基本不再变化。
 下图显示了三种梯度下降算法的收敛过程：
 

4 梯度下降算法的调优方法（目的：加快收敛速度）

当选择好了使用BGD、SGD、MBGD其中一个梯度下降方式后，对下降梯度算法需要进行调优，那么应该从哪些方面进行调优？

4.1 学习速率(Learning Rate)α调优
在θ迭代结算公式中，其中的偏导数的系数α是学习速率（Learning Rate），且α>0。

1）固定的α，α太大的话，导致迭代次数变少(因为θ增量变大)，学习速率变快，训练快。但是α不是越大越好，如果α太大的话，会导致梯度下降算法在图形的上坡和下坡上面来回震荡计算，严重的结果可能无法收敛；

2）固定的α，α太小的话，导致迭代次数变多(因为θ增量变小)，学习速率变慢，训练慢。但是α不是越小越好，如果α太小的话，会导致梯度下降算法在图形迭代到最优点处整个过程需要训练很长时间，导致训练太慢，虽然可以取得最优θ。

3）变化的α，当梯度大的时候，学习速率变大，梯度小的时候，学习速率变小。则学习速率和梯度是一个正相关，可以提高下降算法的收敛速度。α和梯度的正相关有一个比例系数，称为Fixed Learning Rate。Fixed Learning Rate一般取0.1或者0.1附件的值，可能不是最好但是一定不会太差

4.2选取最优的初始值θ
首先，初始值θ不同，获得的代价函数的最小值也可能不同，因为每一步梯度下降求得的只是当前局部最小而已。所以需要多次进行梯度下降算法训练，每次初始值θ都不同，然后选取代价函数取得的最小值最小的那组初始值θ。

4.3特征数据归一化处理
样本不相同，特征值的取值范围也一定不同。特征值的取值范围可能会导致迭代很慢。所以就要采取措施减少特征值取值范围对迭代的影响，这个措施就是对特征数据归一化。

数据归一化方法有：1）线性归一化，2）均值归一化。一般图像处理时使用线性归一化方法，比如将灰度图像的灰度数据由[0,255]范围归一化到[0,1]范围。如果原始数据集的分布近似为正态（高斯）分布，那么可以使用均值归一化对数据集进行归一化，归一化为：均值为0，方差为1的数据集。这里面采用均值归一化，均值归一化的公式如下所示：

其中μ是原始数据集的均值，σ是原始数据的标准差，求出来的归一化数据的特点是：均值为0，方差为1的数据集。

经过特征数据归一化后，梯度下降算法会在期望值为0，标准差为1的归一化特征数据上进行迭代计算θ，这样迭代次数会大大加快