分类模型评价指标:精确率、召回率及P-R曲线、ROC曲线具体实现(附详尽代码)

1.评价指标定义(二分类)

对于二分类问题，可将样例根据其真实类别与学习器预测的类别组合成混淆矩阵。在该矩阵中，矩阵中的行代表样例的真实类别，矩阵中的列代表预测器预测的类别(行和列所代表的可以互相交换)。利用混淆矩阵，可以将样本分为以下四种：

真实类别	预测类别
	正例	负例
正例	TP(真正例)	FN(假反例)
负例	FP(假正例)	TN(真反例)

真正例：真实为正样本，预测也为正样本。假反例：真实为正样本，预测为负样本。

假正例：真实为负样本，预测为正样本。真反例：真实为负样本，预测也为负样本。

从上述四个定义可以发现，只有真正例和真反例对应的样本才是模型正确预测的。基于这四类样本，延伸出了以下模型评价指标：

• 精确率(P)：又叫查准率。描述的是实际为正的样本占所有预测为正的样本的比例。即，所有预测为正的样本中有多少样本实际也为正。其公式为：P  =TP/(TP+FP)。
• 召回率(R)：又叫查全率。描述的是预测为正的样本占所有实际为正的样本的比例。即，所有实际为正的样本中有多少样本被预测为正。其公式为：R=TP/(TP+FN)
• P-R曲线：根据模型的预测结果对记录进行排序，按此顺序逐个将记录作为正样本进行预测，计算出精确率和召回率。然后以精确率为纵坐标，召回率为横坐标。然后将点连成线即可。
• F1值是精确率和召回率的调和均值：2/F1=1/P+1/R
• 真正率(TPR):TPR=TP/(TP+FN)。即，所有实际为正的样本中也被预测为正的样本的比例。
• 假正率(FPR):FPR=FP/(TN+FP)。即，所有实际为负的样本中被预测为正的样本的比例。
• ROC曲线：与P-R曲线类似，只不过其纵坐标为真正率，假正率为横坐标。然后将点连成线即可。
• AUC值；坐标系中ROC曲线的面积。

2. 代码实现

这部分主要是想自己写代码实现上述指标的计算。在以下代码中，模型的训练及学习会直接调用sklearn中的包来实现。各个指标及曲线的实现则用自己的代码实现。以UCI中的乳腺癌数据集为例，使用逻辑回归模型训练数据。另外，鉴于这里的目的并不在于模型的训练过程，所以这里把整个数据集中的数据都作为训练数据，不再抽取样本作为测试集。以1为zheng

2.1 取数及模型训练

from sklearn.datasets import load_breast_cancer
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
#取出数据集,X即为feature对应的数据，y即为类标记数据
X,y=load_breast_cancer(return_X_y=True)
#训练模型
LR=LogisticRegression(random_state=0).fit(X,y)
#现在将数据投入到模型中，然后将模型预测的结果输出。
#LR.predict()函数会直接返回模型对每一条数据给出的预测的类标签
#LR.predict_proba()这个函数会返回每一条数据被预测成正负类的概率。
result=pd.DataFrame(LR.predict_proba(X),columns=LR.classes_).join(pd.Series(LR.predict(X),name='pre_target'))
#实际结果
result['target']=y
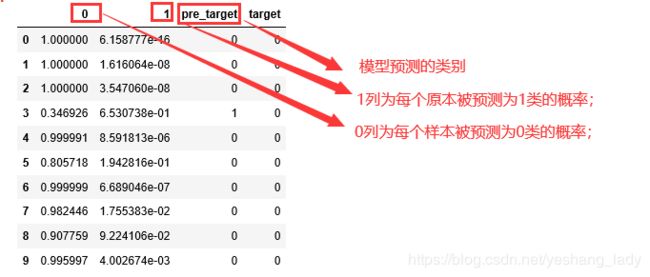
result.head(10)

result的结果如下：

对result做简单分析可以发现，对每一样本而言，0列和1列中的较大值所对应的类别即为模型的预测类别。

下面先来构造混淆矩阵。具体代码如下：

#先计算TP,TN,FP,FN,并构建混淆矩阵。把类别1当作正样本
TP=result[(result['pre_target']==1)&(result['target']==1)].shape[0]
TN=result[(result['pre_target']==0)&(result['target']==0)].shape[0]
FP=result[(result['pre_target']==1)&(result['target']==0)].shape[0]
FN=result[(result['pre_target']==0)&(result['target']==1)].shape[0]
#这里用Dataframe来展示混淆矩阵
rix_result=pd.DataFrame(np.array([[TP,FN],[FP,TN]]),\
                           index=[['real_target','real_target'],[1,0]],
                          columns=[['pre_target','pre_target'],[1,0]])
matrix_result

其结果如下：

 接着计算精确率、召回率、F1值、真正率和假正率。具体代码如下：

P=TP/(TP+FP)
R=TP/(TP+FN)
F1=2*(P+R)/(P*R)
FPR=FP/(TN+FP)
print("精确率R,真正率TPR: {:.3f}".format(P))
print("召回率:{:.3f}".format(R))
print("F1值:{:.3f}".format(R))
print("假正率:{:.3f}".format(FPR))

代码运行结果如下：

 再来看P-R曲线。具体代码如下：

import matplotlib.pyplot as plt
pr_data=result[['1','target']]
pro_data=sorted(pr_data['1'],reverse=True)
dict_1={'P':[],'R':[]}
for pro in pro_data:
    pr_data['pre_target']=(pr_data.loc[:,'1']>=pro).astype("int")
    pr_data['pre_target'].value_counts()
    TP=pr_data[(pr_data['pre_target']==1)&(pr_data['target']==1)].shape[0]
    TN=pr_data[(pr_data['pre_target']==0)&(pr_data['target']==0)].shape[0]
    FP=pr_data[(pr_data['pre_target']==1)&(pr_data['target']==0)].shape[0]
    FN=pr_data[(pr_data['pre_target']==0)&(pr_data['target']==1)].shape[0]
    P=TP/(TP+FP)
    R=TP/(TP+FN)
    dict_1['P'].append(P)
    dict_1['R'].append(R)
plt.plot(dict_1['R'],dict_1['P'],color='darkorange',label='P-R')
plt.xlabel("Recall Rate")
plt.ylabel("Persion Rate")
plt.legend()
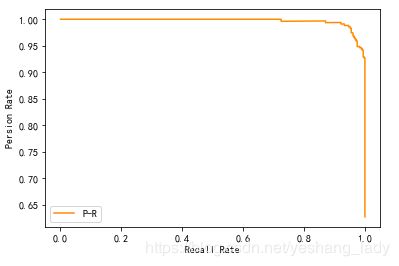
plt.show()

其代码运行结果如下：

再来看ROC曲线(这里只画ROC曲线，不讨论AUC值的计算)。具体代码如下：

import matplotlib.pyplot as plt
pr_data=result[['1','target']]
pro_data=sorted(pr_data['1'],reverse=True)
dict_1={'TPR':[],'FPR':[]}
for pro in pro_data:
    pr_data['pre_target']=(pr_data.loc[:,'1']>=pro).astype("int")
    pr_data['pre_target'].value_counts()
    TP=pr_data[(pr_data['pre_target']==1)&(pr_data['target']==1)].shape[0]
    TN=pr_data[(pr_data['pre_target']==0)&(pr_data['target']==0)].shape[0]
    FP=pr_data[(pr_data['pre_target']==1)&(pr_data['target']==0)].shape[0]
    FN=pr_data[(pr_data['pre_target']==0)&(pr_data['target']==1)].shape[0]
    TPR=TP/(TP+FN)
    FPR=FP/(FP+TN)
    dict_1['TPR'].append(TPR)
    dict_1['FPR'].append(FPR)
plt.plot(dict_1['FPR'],dict_1['TPR'],label='ROC曲线')
plt.plot(dict_1['FPR'],dict_1['FPR'],linestyle='--')
plt.xlabel('FPR')
plt.ylabel("TPR")
plt.legend()
plt.show()

结果如下：

 注意及总结：

• 首先要注意的是，本部分计算的各个指标值P,R及P-R曲线、ROC曲线的值都接近理想状态，这里主要是因为这些指标及曲线所使用的数据都来自于训练集。任何模型在训练集上的结果都是非常好的(模型训练的目的就是找到一组参数可以使其在训练集上的损失函数最小，损失函数最小，分类正确的就越多)。
• LR模型中的预测结果可以理解为：当该条记录被预测为1的概率大于某个阈值是为类别1，否则为类别2。而在LR模型中该阈值默认为0.5。如果我们不断改变阈值，则对应的预测结果也会发生改变，每一组预测结果对应一组评价指标，将相关评价指标的关系用图形展示出来，就形成了P-R曲线和ROC曲线。

3.sklearn包实现

from sklearn.datasets import load_breast_cancer
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix,f1_score,precision_score,recall_score,\
                precision_recall_curve,roc_curve,roc_auc_score
#取出数据集,X即为feature对应的数据，y即为类标记数据
X,y=load_breast_cancer(return_X_y=True)
#训练模型
LR=LogisticRegression(random_state=0).fit(X,y)
#计算混淆矩阵
y_pre=LR.predict(X)
con_matrix=confusion_matrix(y,y_pre)
P=precision_score(y,y_pre,average='binary')
R=recall_score(y,y_pre,average='binary')
F1=f1_score(y,y_pre,average='binary')
precision,recall,_=precision_recall_curve(y,y_pre)
fpr,tpr,_=roc_curve(y,y_pre)
auc=roc_auc_score(y,y_pre)

这里结果就不展示了，需要说明的一点是，P-R曲线和ROC曲线的结果与第2部分中只是趋势一致。这主要是因为sklearn包中roc_curve的方法只返回了三组（fpr,tpr)值，精度不够。