Python3学习笔记：算法：广度优先搜索（BFS）算法

一、广度优先搜索算法

图的广度优先搜索算法（Breadth-First Search）是一个分层遍历的过程，类似树的层序遍历。

基本思想：从图中的某一个顶点V出发，访问此顶点后，依次访问顶点V的各个同层未访问过的邻接点，然后分别从这些邻接点出发，直至图中所有顶点都被访问到。该算法探索所有顶点的所有邻接点，并确保每个顶点只访问一次，没有访问两次的顶点。

例如：首先访问 v1 和 v1 的邻接点v2 和v3，然后依次访问v2 的邻接点v4 和v5 及v3 的邻接点v6 和v7，最后访问v4 的邻接点v8。由于这些顶点的邻接点均已被访问，并且图中所有顶点都被访问，因此完成了图的遍历；得到的顶点访问序列为：v1→v2 →v3 →v4→ v5→ v6→ v7 →v8。

      在遍历顶点的过程中需要一个访问标志数组，标志哪些顶点已被访问；并且，为了顺次访问路径长度为2、3、…的顶点，需附设队列以存储已被访问的路径长度为1、2、… 的顶点。

二、算法实现

 1""" 2graph 使用字典实现 { 顶点：连接顶点列表} 3键key是图中顶点 4值value是与顶点相连接的顶点组成的队列 5""" 6def bfs_search(graph,start_point): 7    # 顶点无效、图无效、连接顶点为空，算法结束 8    if start_point  not in graph: 9        return None10    if graph[start_point] is None:11        return None12    if graph[start_point] == []:13        return None14    # 队列：存储待访问顶点15    queue = [start_point]16    # 集合：存储已访问顶点17    visited = set()18    # 待访问顶点队列不为空，则循环继续19    while queue:20        # 访问队列第一个顶点21        point = queue.pop(0)22        if point not in visited:23            # 顶点未访问，加入已访问集合24            visited.add(point)25            # 连接顶点队列扩充到未访问队列26            # extend() 函数用于在列表末尾一次性追加27            # 另一个序列中的多个值（用新列表扩展原来的列表）28            # graph[point]为连接顶点，去掉已访问的顶点29            queue.extend(graph[point] - visited)3031    return visited

 

三、最短路径

最小路径Path可以通过广度优先搜索算法找到，算法使用两个队列，即Q1和Q2。 Q1保存要处理的所有顶点，而Q2保存从Q1处理和删除的所有顶点。

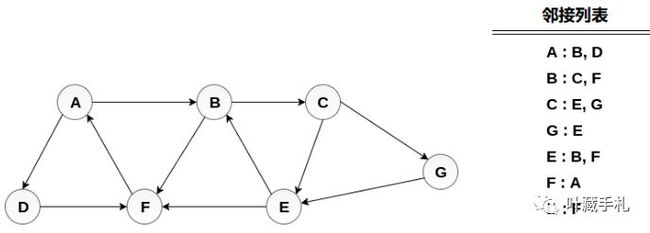
问题：计算从顶点A到顶点E的最小路径p

第1步：将A加入Q1，Q2为空

Q1：A

Q2

第2步：将A从Q1删除、加入Q2，将A的邻接顶点B、D加入Q1

Q1：B、D

Q2：A

第3步：将B从Q1删除、加入Q2，将B的邻接顶点C、F加入Q1

Q1：D、C、F

Q2：A、B

第4步：将D从Q1删除、加入Q2，由于D的邻接顶点F已经加入Q1，不重复加入。

Q1：C、F

Q2：A、B、D

第5步：将C从Q1删除、加入Q2，将C的邻接顶点E、G加入Q1

Q1：F、E、G

Q2：A、B、D、C

第6步：将F从Q1删除、加入Q2，由于F的邻接顶点A已经处理过，不重复加入。

Q1：E、G

Q2：A、B、D、C、F

第7步：将E从Q1删除、加入Q2，由于E的邻接顶点B、F已经处理过，不重复加入。

Q1：G

Q2：A、B、D、C、F、E

顶点E是目标顶点，在Q2中从目标顶点E回溯到起始顶点A，即：从A到E的最短路径。

从顶点A到顶点E的最小路径p为：A→B→C→E。

品略图书馆 http://www.pinlue.com/