灰度共生矩阵 Gray-Level Co-occurrence Matrix(GLCM)原理（一）
目录
重要概念
GLCM属性
1. 该矩阵是方形的，即N*N大小，一般为8*8, 16*16,32*32
2.它的行数和列数与图像的量化级别相同。
3. 该矩阵沿对角线对称。
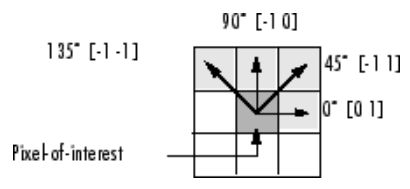
4. offset位移，距离 ,定义为[row_offset, col_offset]
如何产生对称的共生矩阵GLCM图例说明
水平方向共生矩阵
垂直方向共生矩阵
归一化公式
产生对称的共生矩阵GLCM总结
官方说明
重要概念
neighbour pixel: 共生点
ref pixel:参考点，基准点
灰度共生矩阵（GLCM）：是一种统计表格，不是一幅图片
GLCM属性
1. 该矩阵是方形的，即N*N大小，一般为8*8, 16*16,32*32
2.它的行数和列数与图像的量化级别相同。
如果图片是8位深度，即灰度范围[0,255]共
个级别（level），那么行数与列数都是256；但是这样的矩阵计算量太大，一般会缩放至
或
个级别，也有
个级别的。
3. 该矩阵沿对角线对称。
如果共生点对(0,2)在图片中出现了一次【往东边计算】，那么反过来，往西边计算，共生点对(2,0)在图片中也出现一次。
这样做的目的是：最东边的元素没有右边的共生点可以计算，而最西边的元素没有左边的共生点，让共生矩阵对称后就不会有此问题。
换句话说，就是从东往西计算一次，再从西往东计算一次。【参考offset位移，距离 ,定义为[row_offset, col_offset]】
以下面的原始图为例，以共生点对（0,2）为例，从东往西(0,2)计算出现一次，从西往东(2,0)计算也出现一次，这时不用管谁在左谁在右，只要它们之间的距离是1就行。即水平方向它们出现两次。
问：如何让共生矩阵对称？
答：把产生的统计矩阵 与 它的转置矩阵（transpose）相加，即得到对称的共生矩阵。
4. offset位移，距离 ,定义为[row_offset, col_offset]
此处借用MATLAB的图。
坐标系如下，注意方括号里的值代表的是[row, col]【即（y, x）】上对应的位移，与OpenCV的图片坐标表示是一样的。
如果要产生对称的GLCM，需要计算八个方向【东&西、南&北、东北&西南、西北&东南】；
不对称的GLCM，只需计算四个方向【东、东北、北、西北】
如何产生对称的共生矩阵GLCM图例说明
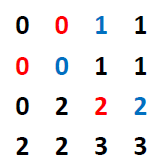
原始图：
水平方向共生矩阵
Framework matrix 框架矩阵（组合矩阵）：
东边（右边）方向的共生点对(0,0) (0,1) (2,2)【(参考点，共生点)】【注意：（2,2）出现了三次】
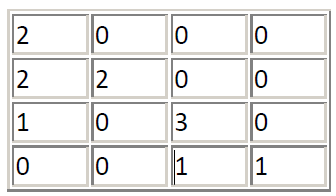
参考点东边E(1,0)的共生统计结果如下，记为原矩阵 O ：
将上面矩阵转置得到下面的转置矩阵T
原矩阵 O 与转置矩阵 T 相加，得到水平方向的共生矩阵，其中共生点对之间的距离为1。
这个共生矩阵有效点对的次数为4+2+1+2+4+1+6+1+1+2=24，而共生点对（2,2）共出现了6次。
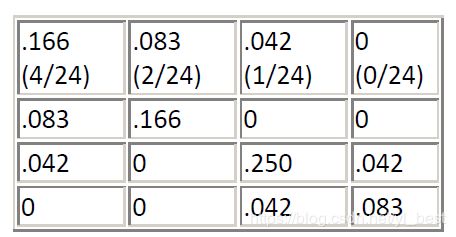
那么共生点对(2,2)出现的概率为6/24=1/4 即25%, 共生点对(2,3)的出现概率为1/24=4.2%.
最后一步：归一化
每个格子的值(Value)除以总数（sum）就得到概率矩阵。
上面水平方向的共生矩阵中总数为24，归一化后即得到如下矩阵
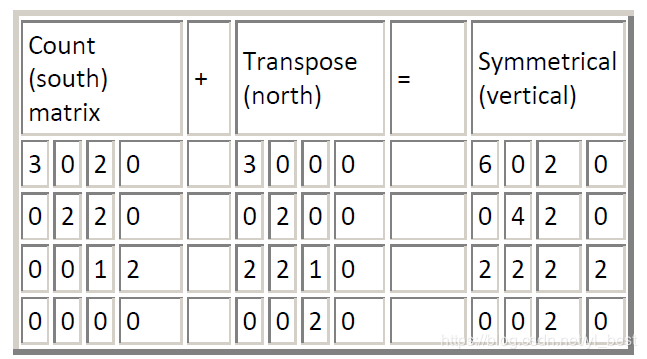
垂直方向共生矩阵
Count(south) matrix + Transpose(north) matrix = Symmetrical(vertical) matrix
参考点南边（0,1）的矩阵 + 转置矩阵 = 垂直方向上对称的共生矩阵
概率矩阵：垂直方向上的对称共生矩阵归一化之后的结果如下：
归一化公式
产生对称的共生矩阵GLCM总结
产生对称的共生矩阵的步骤：
1. Create a framework matrix taking into account the bit depth【考虑图像位深、灰度级别，建立一个框架矩阵】
2. Decide on the spatial relation between the reference and neighbour pixel【确定参考像素与共生像素的空间关系，如水平方向--东、垂直方向 -- 北、对角线方向--东北、对角线方向--东南等】【注意：只考虑一个方向】
3. Count the occurrences and fill in the framework matrix【计算点对的出现次数，并填入矩阵中，得到原矩阵 O】
4. Add the matrix to its transpose to make it symmetrical【将原矩阵 O 的转置矩阵 T 加到 原矩阵 O 中，产生对称的共生矩阵】
5. Normalize the matrix to conceptually turn it into probabilities.【归一化，转为概率矩阵】
官方说明
1、https://www.mathworks.com/help/images/ref/graycomatrix.html
【灰度共生矩阵原理，步距、方向原理等说明，及MATLAB代码】
2、https://prism.ucalgary.ca/handle/1880/51900
【一本入门教程，可以下载为pdf小册子，里面有详细的范例《GLCM Texture: A Tutorial v. 3.0 March 2017》】
3、Haralick, R.M., K. Shanmugan, and I. Dinstein, "Textural Features for Image Classification", IEEE Transactions on Systems, Man, and Cybernetics, Vol. SMC-3, 1973, pp. 610-621. 【方法提出者】