海明校验 详细代码及算法分析(Python)

背景介绍

海明码由Richard Hamming于1950年提出、目前还被广泛采用的一种很有效的校验方法，是只要增加少数几个校验位，就能检测出二位同时出错、亦能检测出一位出错并能自动恢复该出错位的正确值的有效手段，后者被称为自动纠错。它的实现原理，是在k个数据位之外加上r个校验位，从而形成一个k+r位的新的码字，使新的码字的码距比较均匀地拉大。把数据的每一个二进制位分配在几个不同的偶校验位的组合中，当某一位出错后，就会引起相关的几个校验位的值发生变化，这不但可以发现出错，还能指出是哪一位出错，为进一步自动纠错提供了依据。
这种能找出并纠正数据块在传输过程中出现的错误的编码方法，对于计算机技术和通信技术来说真是太重要了。发明这种编码技术的理查德·哈明因此而获得了第三届即1968年度的图灵奖。

海明编码

1.校验位位数

设校验码有k位有效信息和r个校验位，一个校验位P_i要负责监督多个有效位b_i，因此r个校验位就有r个分组，每个可以构成一个指错字，也就是说每个“小组长”需要汇报自己组员的情况，一个组员可以加入多个小组，各个组长的信息综合起来便知道这个成员情况了。
r个校验位可以指出2^r种状态，其中一种表示无错，剩下的状态可以指出2^r-1位中某位的错误。
因此有式子（指出并纠正一处错误）：
$$k+r\le 2^r-1$$
把r移到右边去：
$$k\le 2^r-r-1$$

2.分组原则

为了方便最后算出哪一位出错，我们把位号为2ⁿ(n = 0, 1, 2, …)的位置全部留给校验位，其他的安放有效位，两者相互穿插组成海明码(Hamming Code)。
e.g.
k = 7, r = 4

位号	1	2	3	4	5	6	7	8	9	10	11
内容	P1	P2	b1	P3	b2	b3	b4	P4	b5	b6	b7

之后再看分组规则：
第i位由位号和=i的校验位组成
e.g.
7 = 1 + 2 + 4
对于P_i而言有：P_i = 2^i-1(i≥1)
故：b₄ = P₁ + P₂ + P₃
而由于b₄组分之一是P₁，故P₁的分组里包含b₄。

再举个例子：
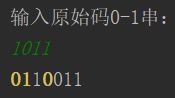
设有效信息为b₁b₂b₃b₄ = 1011，其中k=4，k ≤ 2³ - 3 - 1，因此取最小的r为3。
3 = 1 + 2， 5 = 1 + 4， 6 = 2 + 4， 7 = 1 + 2 + 4
参考上表可得：
$$P_1=b_1⨁b_2⨁b_4=1+0+1=0$$
$$P_2=b_1⨁b_3⨁b_4=1+1+1=1$$
$$P_3=b_2⨁b_3⨁b_4=0+1+1=0$$
最终得到了海明码：0110011

3.代码实现

先来定义程序所需要的类，分别为有效位和校验位，属性有：P和b的角标号num，位数值bit，相关联位的下标的列表link。

class valid_bit:  # 有效位
    def __init__(self, b, i):
        self.num = i  # 序号
        self.bit = int(b)  # 数值
        self.link = []  # 组成成分，7 = 4 + 2 + 1

class check_bit:  # 校验位
    def __init__(self, i):
        self.num = i  # 序号
        self.bit = None  # 数值
        self.link = []  # 校验位

函数smallest_check_number的作用是根据k返回所需要校验位的最小数目r。

def smallest_check_number(k):
    r = 1
    while 2 ** r - r - 1 < k:
        r += 1  # 得到最小检测位数
    return r

现输入一个0-1字符串string，传入hamming_encode函数进行编码，得到海明码。检查输入字符串是否合乎规范很简单，看’1’和’0’的数目之和和len(string)等不等，一句话搞定。

def is_standard(string):
    return string.count('1') + string.count('0') == len(string)

可先令有效位在存储位信息的list中就位，再调用list的insert方法，将校验位插入位号为2ⁿ的位置，非常方便。见下图演示。
再引入checkList按顺序存储校验位的位号，以便在后面为位确定相互的联系并分组。
代码如下：

    hammingList.append(0)  # 填补0位，index即下标
    for i in range(1, len(string) + 1):
        locals()['b' + str(i)] = valid_bit(int(string[i - 1]), i)
        hammingList.append(locals()['b' + str(i)])  # 先加入b
    r = smallest_check_number(len(string))
    for j in range(1, r + 1):
        locals()['P' + str(j)] = check_bit(j)
        hammingList.insert(2 ** (j - 1), locals()['P' + str(j)])
        checkList.append(2 ** (j - 1))  # 再插入P

然后确定有效位b_i的位号由哪些P_j的位号组成。
例如：b₄的位号是2的3次方减1，得7，我们之前定义的checkList里面存储的校验位号为[1, 2, 4, 8],于是将7从大到小减去checkList中的元素，直到为0。

伪码分析：
7 < 8: continue
7 ≥ 4: 7 - 4 = 3, link.append(4)
3 ≥ 2: 3 - 2 = 1, link.append(2)
1 ≥ 1: 1 - 1 = 0, link.append(1)
0 == 0: end

于是b₄这个对象的link属性为[4, 2, 1]，意味着b₄受这三个校验位“管教”。
接下来位号4对应的P₃的属性link也append一个7，相当于P₃的小组加入了成员b₄；P₂的link也加入一个7；P₁同理。
可见在这个过程，把b和P的这种相互关系确定了。

    for i in range(1, len(hammingList)):  # i是有效位，j是检测位
        if i in checkList:
            continue  # 跳过P
        remain = i
        for j in range(len(checkList) - 1, -1, -1):
            if remain >= checkList[j]:
                remain -= checkList[j]
                hammingList[i].link.append(checkList[j])  # b的link中加入P的位号
            if remain == 0:
                break
        for j in hammingList[i].link:
            hammingList[j].link.append(i)  # P的link中加入b的位号

最后计算校验码的值，把None给覆盖掉。计算非常简单，因为class为check_bit的对象可通过属性轻松找到所关联的全部有效位。

    for j in checkList:
        xor = 0
        for i in hammingList[j].link:
            xor = xor ^ hammingList[i].bit
        hammingList[j].bit = xor

打印编码后的海明码，校验位全部高亮显示（checkList又派上用场了）。

    for i in range(1, len(hammingList)):
        if i in checkList:  # 检测码
            print('\033[1;33m%d\033[0m' % hammingList[i].bit, end='')
        else:
            print('%d' % hammingList[i].bit, end='')

4.最终效果

海明校验

1.查错与纠错原理

海明编码被分为r组校验，每组产生一个检错信息G_i,r个检错信息组成一个指错字：G_rG_r-1…G₂G₁，举例而言：
$$G_3=P_3⨁b_2⨁b_3⨁b_4$$
类似地：G_i = P_i 异或所有关联的b。实际上，G_i相当于信息传输前后的两组数位相异或，若有一个数位出错，结果为1，如果所有G都是0，则表示数据没有出错，反之则表示第G_rG_r-1…G₂G₁位数据有误。
e.g.
G₃G₂G₁ = 010表示第2位数据有误，翻转即为正确结果。

2.代码实现

和hamming_encode函数类似，hamming_correct函数最开始也要解析输入的字符串，区别在于，这里输入的string是海明码而非有效信息，所以要根据len(string)反推k和r的值。

    k = 1
    while k + smallest_check_number(k) != len(string):  # 反推r和k
        k += 1
    r = smallest_check_number(k)

计算指错字的大小，用队列去存G比较方便，这里我还是用的list从低位到高位存储，然后遍历列表累加乘方值得到最终结果，并修正结果。

    G_List = []  # 指错字列表
    for j in checkList:
        xor = hammingList1[j].bit  # 本身
        for i in hammingList1[j].link:
            xor = xor ^ hammingList1[i].bit
        G_List.append(xor)
    bit = 0
    sum = 1
    for i in range(len(G_List)):
        bit += sum * G_List[i]
        sum *= 2
    if bit == 0:
        print("未出错")
        return
    else:
        hammingList1[bit].bit ^= 1  # 翻转

打印修正后的海明码，代码略。

3.最终效果

在编码功能里随便输入个"011010111001"，得到"10001100101110011"。

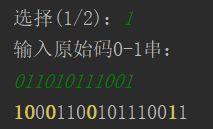
再把结果原封不动输到纠错功能里，显示“未出错”。

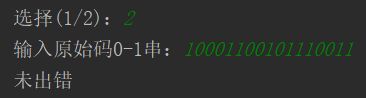
该结果随便改一位数，并去验错，显示了正确结果并高亮了错误位。

总结

今天上了一节组原，讲了Hamming Code，对它的代码实现比较感兴趣，于是给自己出了个题目去玩，写得很匆忙，代码不是很elegant，本人才疏学陋，见谅了。在论坛没有发现啥有意思的博客，所以想发上来，也是第一次在CSDN写东西。海明码这么妙的编码真的很启发人，所以平时要多去思考计算机深层次的原理，在较高的维度上设法优化算法，这是件很有意思也很有意义的事情。

exe可执行文件下载链接
链接：https://pan.baidu.com/s/1F7I-ktaRekUcENm4ULxu6A
提取码：771j