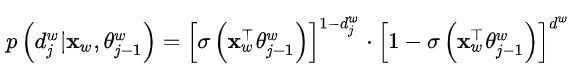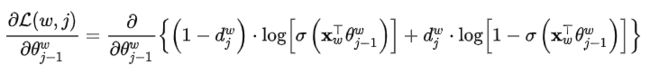个人总结：自然语言处理 word2vec(skip-gram/CBOW以及优化算法Hierarchical Softmax和Negative Sampling)

前言

word2vec，顾名思义，将一个词转化为向量，也经常会看到一个非常相关的词“词嵌入”，也就是word embedding。词嵌入是一类将词从高维空间映射到低维空间的过程的统称，核心思想是将每个词都映射为低维空间(通常K=50-300维)上的一个稠密向量。K维空间的每一维可以看做一个隐含的主题，只不过不像主题模型中的主题那么直观。

假设每篇文章有N个词，每个词映射为K维的向量，那就可以用一个NxK维的矩阵来表示这篇文章。但是实际中直接输入很难获得令人满意的结果，因此还需要在此基础上加工出更高层的特征。传统浅层机器学习模型中，一个好的特征工程可以带来算法效果的显著提升。而深度学习模型正好为我们提供了一种自动进行特征工程的方式，每个隐层都可以认为对应不同抽象层次的特征。从这个角度来讲深度学习能够打败浅层模型也就顺理成章了。卷积神经网络和循环神经网络一方面很好抓住了文本的特征，另一方面又减少了网络中待学习的参数，提高了训练速度，并且降低了过拟合的风险。

谷歌2013年提出了word2vec，是最常用的词嵌入模型。它实际上是一种浅层的神经网络结构，分别有两种结构CBOW(continuous bag of words)和skip-gram。
 

CBOW和Skip-gram

CBOW根据上下文出现的词语来预测当前词的生成概率，w(t)是当前词，w(t-2)、w(t-1)、w(t+1)、w(t+2)是上下文中出现的词：

输入层有上下文词数这么多个神经元，输入层中每个词都由独热编码方式表示，即所有词均表示成一个N维向量，输出层有词汇表大小个神经元，其中N为词汇表中单词的总数。但是用one-hot representation来表示会出现很多问题，最大的问题是词汇表一般都非常大，可达到百万级别，这样每个词都用百万维的向量来表示简直是内存的灾难。并且除了一个位置是1，其他位置全是0，表达效率很低。于是就发明了Distributed representation（这在后面会继续提到，对神经网络模型的改进措施），将词在一个相对较低维的空间进行表达，而这个空间的维度可以我们在训练时自己指定，也就是隐藏层的维度。其实使用onehot，本质上也是从词向量矩阵中提取词对应的词向量（因为只有这个词对应的维度是1）。

隐藏层的神经元个数可以自己指定，K个隐含单元的取值可以由N维输入向量以及连接输入和隐含单元之间的NxK维权重矩阵计算得到，也就是embedding的维度，这个隐藏层也就是我们的词向量层。在CBOW中，还需要将各个输入词所计算出的隐含单元求和。训练目标是期望训练样本特定词对应的softmax概率最大。

通过在输入层输入上下文的词向量（onehot），将所有词向量分别乘以权重矩阵W，所得的向量相加求平均作为隐层向量，如下

再乘以输出权重矩阵，得到了向量通过softmax得到词汇表的概率分布，再将该概率分布与真实label的onehot作比较，一般采用交叉熵损失函数(本质也是极大似然估计)，这里可以理解为交叉熵损失的一种特殊情况。

这就是我们的损失函数，我们希望极小化它。再使用反向传播，梯度下降法更新W和W’，这就是我们想要的词嵌入矩阵。通过词的onehot向量直接乘以该矩阵就得到了词的嵌入，一般来说使用CBOW，也就是输入层为上下文的词时，使用隐藏层到输出层的权重矩阵作为词嵌入。

以上就是训练过程，通过DNN的反向传播，我们可以训练出DNN模型的参数，同时得到所有词的词向量。这样当我们需要通过上下文预测中心词时，通过一次前向传播以及softmax函数就可以找到概率最大的词对应的神经元。

 

而Skip-gram是根据当前词来预测上下文中各词的生成概率：

对应的输入层只有一个神经元，输出层有N个神经元。隐藏层可以自己指定。最终也是通过softmax函数得到一个概率分布，代表的是在给定单词条件下，其他单词出现的概率，也就是所有。假设我们设置的window=2，中心词为，那么左右两边的上下文可以用，，，，我们的目的是使得条件概率最大，同时假设每个词的出现是相互独立的，于是前面的联合概率可分解成，这其中每个条件概率通过上述得到的softmax概率分布，对应取得。以此作为损失函数（整体概率最大化、极大似然估计），后同样通过DNN的反向传播算法进行训练，可以求出DNN模型参数，同时得到对应的词向量。

但由于softmax存在的归一化项，推导出来的参数的迭代公式需要对词汇表中所有单词进行遍历。这使得每次迭代过程非常非常缓慢，由此产生了Hierarchical Softmax（基于霍夫曼树）和Negative Sampling两种改进方法。训练得到维度为NxK和KxN的两个权重矩阵后，一般来说使用skip-gram，也就是输入层为中心词时，使用输入层到隐藏层的权重矩阵作为词嵌入。

霍夫曼树

Word2vec使用CBOW和skip-gram来训练模型和词向量，但并没有使用传统DNN模型，优先使用的数据结构是霍夫曼树来代替隐藏层和输出层的神经元。霍夫曼树的叶子节点起到输出层神经元的作用，叶子节点的个数为词汇表的大小，树的内部节点起到了隐藏层神经元的作用。

以一个例子说明霍夫曼树的建树过程，假设有(a,b,c,d,e,f)共6个节点，节点的权值分别为(20,4,8,6,16,3)，这些权值一般来说对应它们出现的频率。

霍夫曼树由下向上生长，每次将权值最小的两个节点进行合并，这里先将b和f进行合并，得到新的权值为4+3=7。于是现在的权值更新为20，8，6，16，7。再将权值最小的6和7对应的节点合并，以此类推。

得到霍夫曼树后一般会进行霍夫曼编码，权重高的节点越靠近根节点，权重低的节点会越远离根节点。这样高权重（高出现频率）的节点编码值较短，低出现频率的节点编码值较长（可以将高权重节点理解为常用词，低权重节点理解为稀有词），这符合信息论。霍夫曼编码约定，通过节点之间的边来进行编码，左子树的边编码为0，右子树的边编码为1。于是可以得到c的编码为00，d的编码为010。

在word2vec中，与上述约定相反，左子树的边编码为1，右子树的边编码为0。同时约定左子树权重不小于右子树（与上面图也正好相反）。

 

基于Hierarchical Softmax的模型概述

传统的神经网络词向量模型一般有三层，输入层（词向量，这里还是onehot），隐藏层和输出层（softmax层）。里面最大的问题在于从隐藏层到输出的softmax层的计算量很大，因为要计算所有词的softmax概率，再去找概率最大的值。

word2vec做了一些改进，在输入层到隐藏层的映射，没有采取神经网络的线性变换加激活函数的方法，而是采用简单的对所有输入词向量求和并取平均的方法。同时，这里已经放弃了使用onehot representation，改用了Distributed representation。打个比方，现在输入三个4维的词向量：(1,2,3,4),(9,6,11,8),(5,10,7,12)，映射后的词向量就是(5,6,7,8)。

第二个改进就是从隐藏层到softmax输出层的改进，为了避免计算所有词的softmax概率，word2vec通过霍夫曼树来代替从隐藏层到softmax层的映射。

FastText就采用了hierarchical softmax的优化，总的来说FastText相当于CBOW+h-softmax。其结构为输入-隐层-h-softmax。

如同前面对霍夫曼树的叙述，所有的词都分布在叶子节点上。霍夫曼树的内部节点类似之前神经网络隐藏层的神经元。叶子结点的个数就是词汇表的大小，隐藏层到输出层的softmax映射不是一下子完成的，而是沿着霍夫曼树一步步完成的，因此这种softmax取名为Hierachical Softmax。

我们使用二元逻辑回归的方法，在每一个非叶子节点处都需要做一次二分类，即规定沿着左子树走就是负类（编码1），沿着右子树走就是正类（编码0）。判别正类和负类的方法是使用sigmoid函数

其中为需要从训练样本求出的逻辑回归的参数，为内部节点的词向量。对于上图中的ω2，如果它是一个训练样本的输出，那么期望对于内部隐藏节点n(ω2,1)的P(-)概率大，n(ω2,2)的P(-)概率大，n(ω2,3)的P(+)大。

引入一些符号：

1.：从根节点出发到达w对应叶子节点的路径

2.：路径中包含节点的个数

3.：路径中的各个节点

4. ：词的编码。表示路径第j个节点对应的编码（根节点无编码）

5. ：路径非叶节点对应的参数向量

于是有ω的条件概率，ω为语料中任意一个词

从根节点到叶节点经过了个节点，编码从下标2开始（根节点无编码），对应的参数向量下标从1开始（根节点为1）。

其中

为内部节点的词向量。这里可以采用类似逻辑回归的方式将其写到一起

对目标函数取对数似然：

将代入

通过最大似然对参数进行更新，这里分别最大化内部的每一项。对每个样本，代入偏导数表达式得到函数在该维度上的增长梯度，然后让对应参数加上这个梯度，这就是随机梯度下降法的简单叙述。

分别对参数以及输入词向量求偏导。

最终得到更新表达式为

由于上式损失函数中与是对称的。于是的偏导数为

于是类似，的更新表达式也可以得到了。

通过构造这棵二叉树，将目标概率的计算复杂度从最初的O(V)降低到了O(logV)，由于使用霍夫曼树，更高频的词靠近树根，这样高频词会在更短的时间内被找到。

 

基于Negative Sampling的模型概述

Hierarchical Softmax的缺点

虽然通过霍夫曼树的形式能够提升效率，但是如果训练样本的target word是一个很生僻的词，那么就得在霍夫曼树里往下走很久。也就是说，Hierachical softmax其实是一个不够稳定的算法。而Negative Sampling摒弃了霍夫曼树。

Negative Sampling

假设有一个训练样本，中心词是ω，周围上下文共有2c个词，记为context(ω)，由于这个中心词的确和context相关存在，因此是一个真正的正例。通过Negative Sampling在字典中采样，我们得到neg个和ω不同的中心词ωi，i=1,2，...neg，这样context(ω)和ωi就组成了neg个并不真实存在的负例。利用这一个正例和neg个负例进行二元逻辑回归，得到负采样对应每个词ωi对应的模型参数θi，和每个词的词向量。

如果 vocabulary 大小为10000时， 当输入样本 ( "fox", "quick") 到神经网络时， “ fox” 经过 one-hot 编码，在输出层我们期望对应 “quick” 单词的那个神经元结点输出 1，其余 9999 个都应该输出 0。在这里，这9999个我们期望输出为0的神经元结点所对应的单词为 negative word。 negative sampling的想法也很直接 ，将随机选择集合中一小部分的 negative words，比如选10个 negative words 来更新对应的权重参数。也就是说，输出层的神经元个数由原本的10000个变为了11个，相当于每次只更新300x11=3300个权重参数（假设词嵌入维度为300），对于原来3百万的权重来说，大大提升了计算效率。

论文中作者提出若是小规模数据集，建议选择5-20个negative words，对于大规模数据集选择2-5个negative words。

一个单词背选作negative sample的概率和它出现的频次有关，出现频次越高的单词越容易被选作negative words，经验公式为

f(w)代表每个单词的权重，即词频，分母代表权重和。3/4是个经验参数。