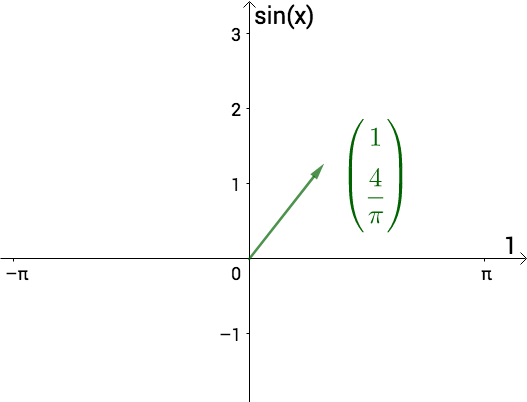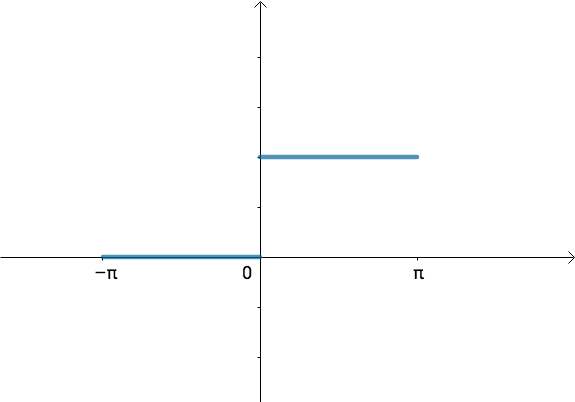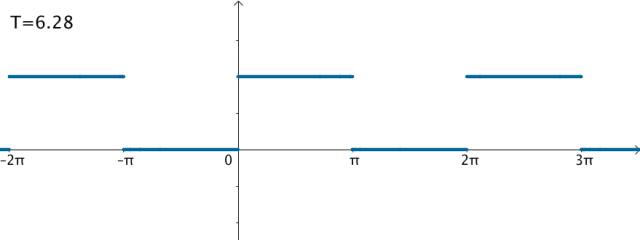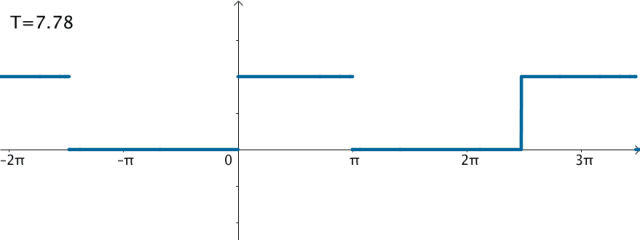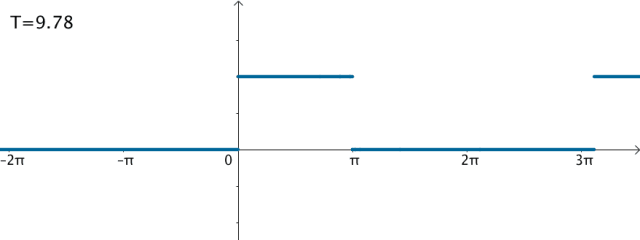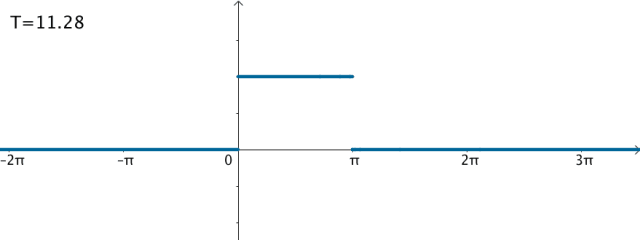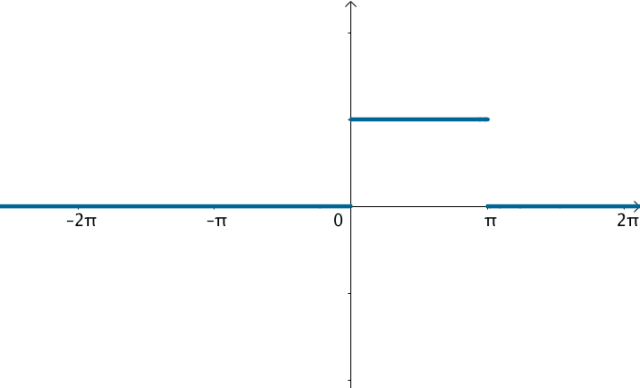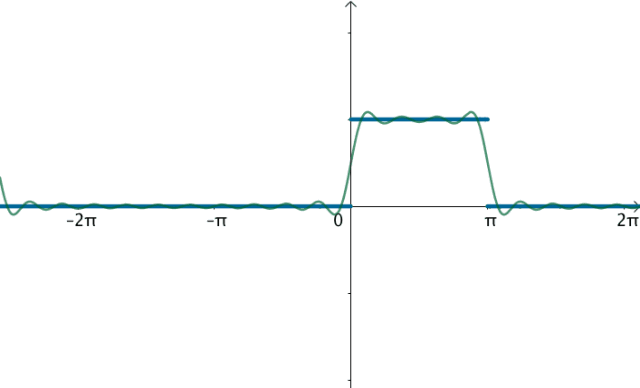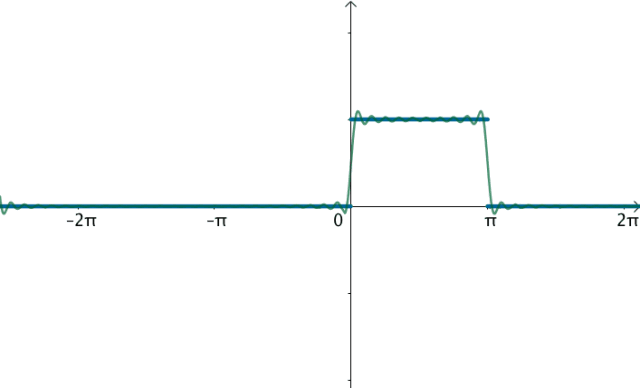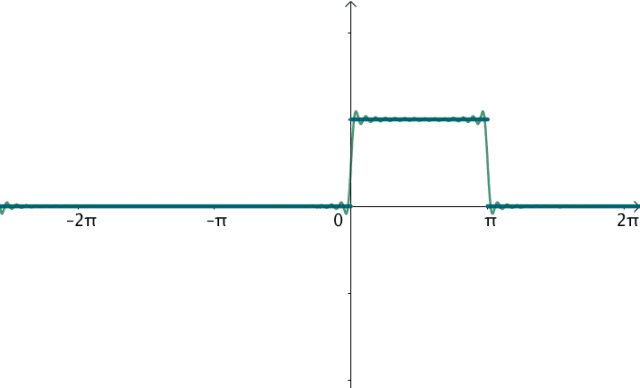从傅立叶级数到傅立叶变换

1. 傅里叶级数的直观意义

如下图，傅里叶级数其实就是用一组sin，cos的函数来逼近一个周期函数，那么每个sin，cos函数就是一组基，这组基上的系数就是频域，会发现随着频域越来越多（基越来越多），函数的拟合就越准确。

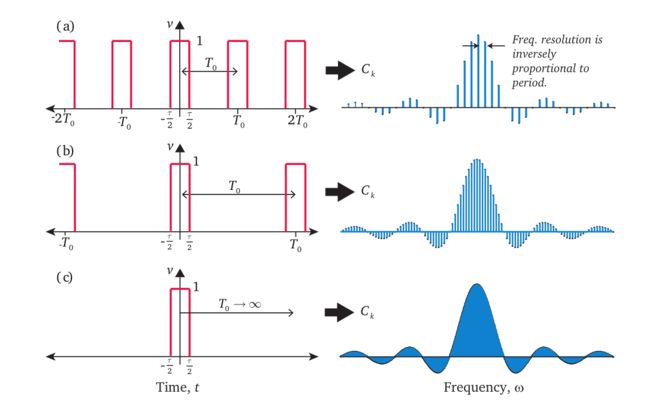
• 周期函数，可以通过傅立叶级数画出频域图
• 增长周期，频域图变得越来越密集
• $T=\infty$，得到傅立叶变换，频域图变为连续的曲线

傅立叶级数是基于周期函数的，如果我们把周期推广到$T=\infty$ ，那么也就变为了非周期函数，这就是傅立叶变换。

2. 傅里叶变换推导

让·巴普蒂斯·约瑟夫·傅里叶男爵（1768 －1830）猜测任意周期函数都可以写成三角函数之和。比如下面这个周期为$2\pi$的方波，可以用大量的正弦波的叠加来逼近：

2.1 傅立叶级数是向量

从代数上看，傅立叶级数就是通过三角函数和常数项来叠加逼近周期为T的函数f(x)。要讲傅里叶变换的推导，先从傅里叶级数讲起，考虑一周期等于T，现定义于区间[-T/2,T/2]的周期函数f(x)，傅里叶级数近似的表达式如下:

$$f(x)=a_0+\sum _{n=1}^{\infty }\left(a_{n}cos(\frac{2\pi n}{T}x)+b_{n}sin(\frac{2\pi n}{T}x)\right),a_0\in \mathbb{R}$$

前面已经推导过，实际上是把f(x)当作了如下基的向量：

$$\{1,cos(\frac{2\pi n}{T}x),sin(\frac{2\pi n}{T}x)\}$$
那么上面的式子就可以解读为：

$$f(x)=\underset{\text{基1下的坐标}}{a_0}\cdot 1+\sum _{n=1}^{\infty }\left(\underset{\text{对应基的坐标}}{a_n}cos(\frac{2\pi n}{T}x)+\underset{\text{对应基的坐标}}{b_n}sin(\frac{2\pi n}{T}x)\right)$$

说具体点，比如刚才提到的，$T=2\pi$的方波f(x)，可以初略的写作：

$$f(x)\approx 1+\frac{4}{\pi }sin(x)$$
从几何上看，有那么一丁点相似：

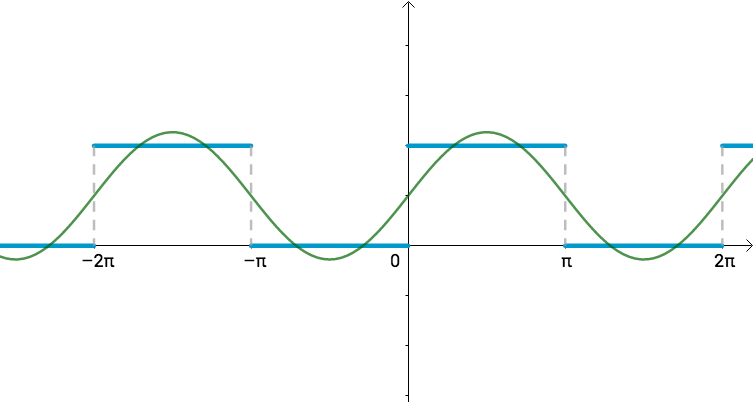
我们可以认为：

$$f(x)\approx 1+\frac{4}{\pi }sin(x)$$

此函数的基为：
{1,sin(x)}
则f(x)相当于向量：
$$(1,\frac{4}{\pi })$$

画到图上如下，注意坐标轴不是x,y，而是1,sin(x)：

2.2 频域图

再增加几个三角函数：

$$f(x)\approx 1+\frac{4}{\pi }sin(x)+0sin(2x)+\frac{4}{3\pi }sin(3x)+0sin(4x)+\frac{4}{5\pi }sin(5x)$$

从几何上看，肯定更接近了：

此时基为：

$$\{1,sin(x),sin(2x),sin(3x),sin(4x),sin(5x)\}$$

对应的向量为：

$$(1,\frac{4}{\pi },0,\frac{4}{3\pi },0,\frac{4}{5\pi })$$

六维的向量没有办法画图啊，没关系，数学家发明了一个频域图来表示这个向量：

上图中的0,1,2,3,4,5分别代表了不同频率的正弦波函数，也就是之前的基：

$$0Hz⟺sin(0x)3Hz⟺sin(3x)\cdots$$

而高度则代表在这个频率上的振幅，也就是这个基上的坐标分量。

这里举的例子只有正弦函数，余弦函数其实也需要这样一个频谱图，也就是需要两个频谱图。当然还有别的办法，综合正弦和余弦。
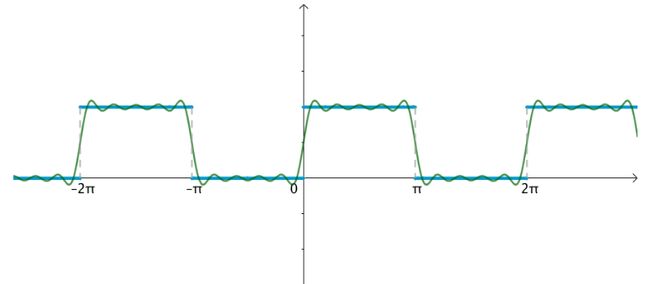
原来的曲线图就称为时域图，往往把时域图和频域图画在一起，这样能较为完整的反映傅立叶级数：

不管时域、频域其实反映的都是同一个曲线，只是一个是用函数的观点，一个是用向量的观点。
当习惯了频域之后，会发现看到频域图，似乎就看到了傅立叶级数的展开：

3. 非周期函数

非周期函数，比如下面这个函数可以写出傅立叶级数吗？

这并非一个周期函数，没有办法写出傅立叶级数。
不过可以变换一下思维，如果刚才的方波的周期：

$$T=2\pi \to T=\infty$$

那么就得到了这个函数：

在这样的思路下，就可以使用三角级数来逼近这个函数:

观察下频域，之前说了，对于周期为T的函数f(x)，其基为：

$$\{1,cos(\frac{2\pi n}{T}x),sin(\frac{2\pi n}{T}x)\}$$

刚才举的方波$T=2\pi$，对应的基就为（没有余弦波）：

$$\{1,sin(x),sin(2x),sin(3x),sin(4x),sin(5x),\cdots sin(nx)\}$$

对应的频率就是：

$$\{0Hz,1Hz,2Hz,3Hz,4Hz,5Hz,\cdots nHz\}$$

按照刚才的思路，如果T不断变大，比如让$T=4\pi$，对应的基就为（没有余弦波）：

$$\{1,sin(0.5x),sin(x),sin(1.5x),sin(2x),sin(2.5x),\cdots sin(0.5nx)\}$$

对应的频率就是：

$$\{0Hz,0.5Hz,1Hz,1.5Hz,2Hz,2.5Hz,\cdots 0.5nHz\}$$

和刚才相比，频率更加密集:

之前的方波的频域图，画了前50个频率，可以看到，随着 不断变大，这50个频率越来越集中：

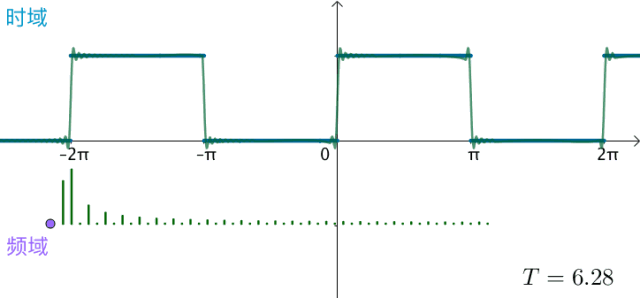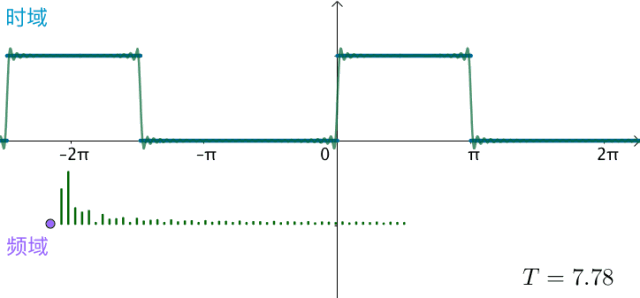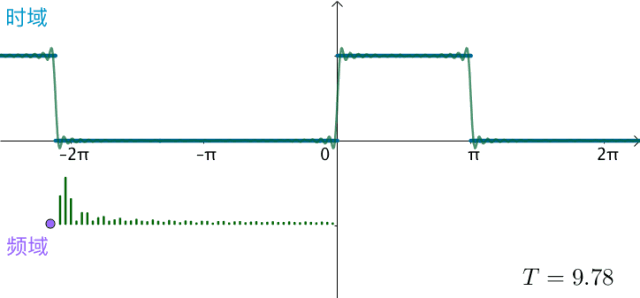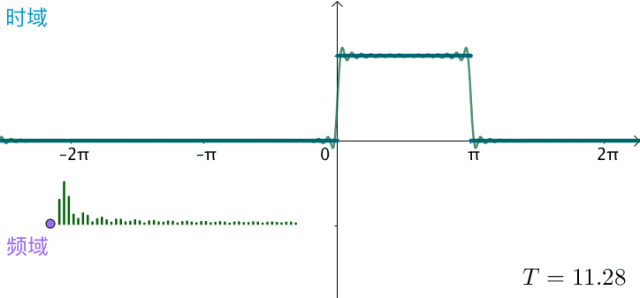
可以想象，如果真的：

$$T=2\pi \to T=\infty$$

这些频率就会变得稠密，直至连续，变为一条频域曲线：

4. 傅立叶变换

之前说了，傅立叶级数是：
$$f(x)=a_0+\sum _{n=1}^{\infty }\left(a_{n}cos(\frac{2\pi n}{T}x)+b_{n}sin(\frac{2\pi n}{T}x)\right),a_0\in \mathbb{R}$$

这里有正弦波，也有余弦波，画频域图也不方便，通过欧拉公式，可以修改为复数形式（见如何理解傅立叶级数公式）：

$$f(x)=\sum _{n=-\infty }^{\infty }{c}_n\cdot e^{i\frac{2\pi nx}{T}}$$

其中：
$$c_n=\frac{1}{T}{\int }_{x_0}^{x_0+T}f(x)\cdot e^{-i\frac{2\pi nx}{T}}dx$$

复数形式也是向量，可以如下解读：
$$f(x)=\sum _{n=-\infty }^{\infty }\underset{\text{对应基的坐标}}{c_n}\cdot \underset{\text{正交基}}{e^{i\frac{2\pi nx}{T}}}$$

不过$c_n$是复数，不好画频域图，所以之前讲解全部采取的是三角级数。
周期推向无穷的时候可以得到：

$$\begin{array}{r}f(x)=\sum _{n=-\infty }^{\infty }{c}_n\cdot e^{i\frac{2\pi nx}{T}}\\ T=\infty \end{array}\}⟹f(x)={\int }_{-\infty }^{\infty }F(\omega )e^{i\omega x}d\omega$$

上面简化了一下，用$\omega$代表频率。
$F(\omega )$大致是这么得到的：

$$\begin{array}{r}{c}_n=\frac{1}{T}{\int }_{x_0}^{x_0+T}f(x)\cdot e^{-i\frac{2\pi nx}{T}}dx\\ T=\infty \end{array}\}⟹F(\omega )={\int }_{-\infty }^{\infty }f(x)e^{-i\omega x}dx$$

$F(\omega )$就是傅立叶变换，得到的就是频域曲线。
下面两者称为傅立叶变换对，可以相互转换：

$$f(x)⟺F(\omega )$$

正如之前说的，这是看待同一个数学对象的两种形式，一个是函数，一个是向量。

来源：马同学高等数学
https://www.matongxue.com/