如何理解拉普拉斯变换?
文章目录
- 1 傅立叶变换简介
- 1.1 直角坐标、极坐标
- 1.2 傅立叶变换
- 2 拉普拉斯变换
- 3 变幅三角函数
拉普拉斯变换是对傅立叶变换的推广。关于傅立叶变换,可以看这三篇文章:
- 如何直观地理解傅立叶变换?
- 如何理解傅立叶级数公式?
- 从傅立叶级数到傅立叶变换
1 傅立叶变换简介
1.1 直角坐标、极坐标
大家知道,直角坐标系、极坐标系之间可以相互转换:
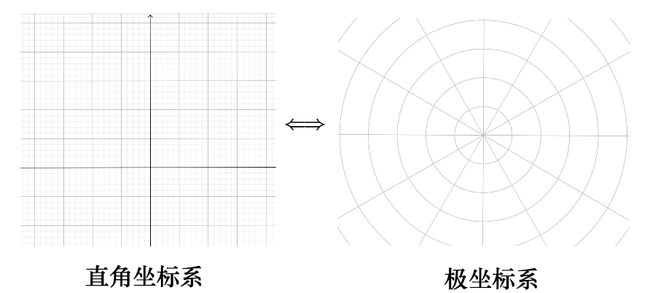
在直角坐标系下,圆的方程为:
x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1
图示如下:

在极坐标系下,同样的圆的方程为:
ρ = 1 \rho=1 ρ=1
图示如下:

如果换到 ρ − θ \rho-\theta ρ−θ坐标系下:

是不是看上去很简单了,从圆变为了一条直线。
同一个数学对象,在不同坐标系中,有不同的表达形式:

1.2 傅立叶变换
傅立叶变换和直角坐标、极坐标的情况类似,相当于换了坐标系。
矩形波在时域“坐标系”中是这样的:
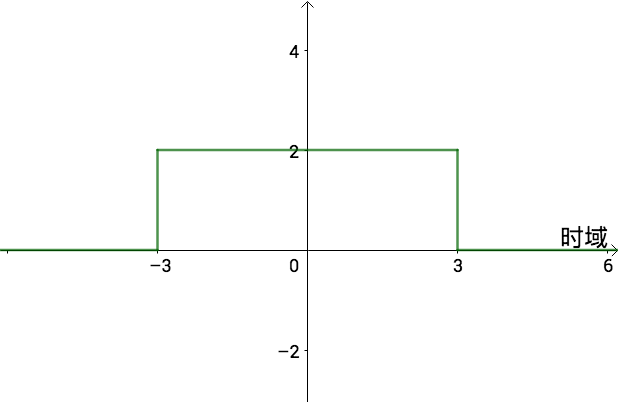
代数形式如下:
f ( x ) = { 2 , − 3 ≤ x ≤ 3 0 , o t h e r w i s e f(x)= \begin{cases} 2,-3\leq x\leq 3\\ 0,otherwise \end{cases} f(x)={2,−3≤x≤30,otherwise
在频域“坐标系”中的图像如下:

代数形式如下(傅立叶变换有很多形式,本文采用下面这种形式):
F ( ω ) = ∫ − ∞ ∞ f ( x ) e − i ω x d x F(\omega)=\int_{-\infty}^\infty f(x)\ e^{-i\omega x}\,dx F(ω)=∫−∞∞f(x) e−iωxdx
也是同一个数学对象,在不同“坐标系”中,有不同的表达方式:

正如在某些情况下,极坐标可以带来计算上的便利,傅立叶变换也可以带来计算上的便利。傅立叶变换难以理解,是因为它所在的“坐标系”更抽象。
2 拉普拉斯变换
傅立叶变换虽然好,但是有一些局限性。我们来看看傅立叶变换的代数式:
F ( ω ) = ∫ − ∞ ∞ f ( x ) e − i ω x d x F(\omega)=\int_{-\infty}^\infty f(x)\ e^{-i\omega x}\,dx F(ω)=∫−∞∞f(x) e−iωxdx
其中, e − i ω x e^{-i\omega x} e−iωx是复平面上绕单位圆旋转的一个向量(点):

总之它是一个有界量。那么上面式子要可积,至少得:
F ( ω ) = ∫ − ∞ ∞ f ( x ) ⏟ 无穷小 e − i ω x ⏟ 有界量 d x F(\omega)=\int_{-\infty}^\infty \underbrace{f(x)}_{\text{无穷小}}\ \underbrace{e^{-i\omega x}}_{\text{有界量}}\,dx F(ω)=∫−∞∞无穷小 f(x) 有界量 e−iωxdx
那,如果 lim x → ∞ f ( x ) = ∞ \lim_{x\to\infty}f(x)=\infty limx→∞f(x)=∞,比如说这样:

这个f(x)的傅立叶变换就没有办法积,是不是非要放弃如此便利的傅立叶变换?
数学家当然不会屈服,至少可以想办法把这个图像拉下来一半:
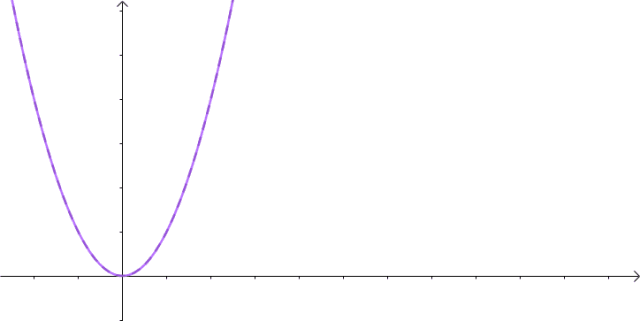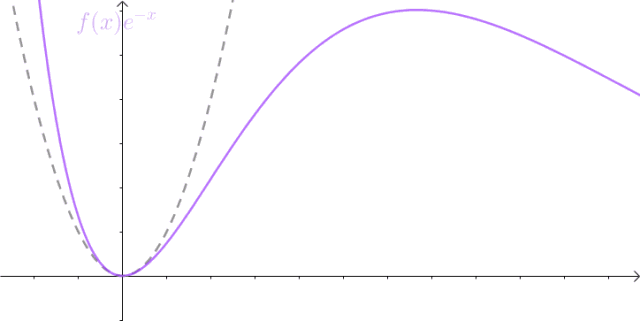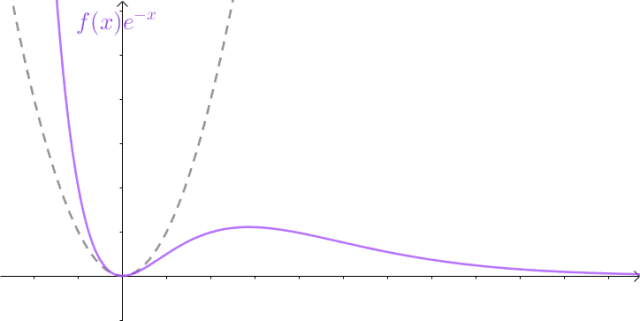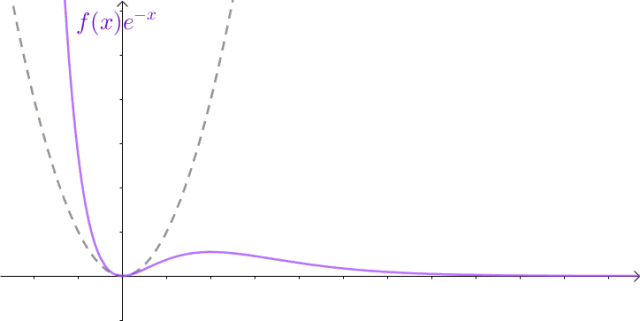
这样:
lim x → + ∞ f ( x ) e − x = 0 \lim_{x\to+\infty}f(x)e^{-x}=0 x→+∞limf(x)e−x=0
为了更好的适应f(x)的各种情况(比如 x x x^x xx增长较快, e − x e^{-x} e−x就扶不住),一般会这么处理:
lim x → + ∞ f ( x ) e − σ x = 0 , σ ∈ R \lim_{x\to+\infty}f(x)e^{-\sigma x}=0,\sigma\in\mathbb{R} x→+∞limf(x)e−σx=0,σ∈R
那么下面积分就可以积了:
F ( ω ) = ∫ 0 ∞ f ( x ) e − σ x e − i ω x d x = ∫ 0 ∞ f ( x ) e − ( σ + i ω ) x d x \begin{aligned} F(\omega) &=\int_{0}^\infty f(x)e^{-\sigma x}\ e^{-i\omega x}\,dx \\ &=\int_{0}^\infty f(x)\ e^{-(\sigma +i\omega)x}\,dx \end{aligned} F(ω)=∫0∞f(x)e−σx e−iωxdx=∫0∞f(x) e−(σ+iω)xdx
令:
s = σ + i ω , σ ∈ R , ω ∈ R s=\sigma +i\omega,\sigma\in\mathbb{R},\omega\in\mathbb{R} s=σ+iω,σ∈R,ω∈R
其实s就是复数了,那么得到:
F ( s ) = ∫ 0 ∞ f ( x ) e − s x d x F(s)=\int_{0}^\infty f(x)\ e^{-sx}\,dx F(s)=∫0∞f(x) e−sxdx
这就是拉普拉斯变换。
当然这个扩展也是付出了代价的,只能在 [ 0 , + ∞ ) [0,+\infty) [0,+∞)上积分,不过影响不大:
- x在应用中,一般代表时间,时间是非负的
- 可以通过双边拉普拉斯变换延展到负轴
3 变幅三角函数
还可以从另外一个角度来看待拉普拉斯变化。
e i ω x e^{i\omega x} eiωx对应的是等幅三角函数(这里用的是 e i ω x e^{i\omega x} eiωx而不是 e − i ω x e^{-i\omega x} e−iωx,请参考“如何理解傅立叶级数公式?”):

而 e s x e^{sx} esx对应的是变幅的、并且振幅越来越大的三角函数:
傅立叶变换用等幅三角函数:
e i ω x e^{i\omega x} eiωx
来逼近原函数,而拉普拉斯用变幅三角函数:
e s x e^{sx} esx
来逼近原函数,这样才能追上高耸入云的 x 2 x^2 x2。
来源:马同学高等数学
https://www.matongxue.com/