隐马尔可夫模型（Hidden Markov Model）

隐马尔可夫模型（HMM）

简述一下HMM：(参考资料：《统计学习方法》-李航)

隐马尔可夫模型（Hidden Markov Model，HMM）描述由隐藏的马尔可夫链随机生成观测序列的过程，属于生成模型。

HMM是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列（状态序列），再由各个状态生成一个观测而产生的观测随机序列（观测序列）的过程。

一堆拗口的术语？下边慢慢道来…

马尔可夫过程

马尔可夫过程指的是：假设一个随机过程中，$t+1$时刻的状态$i_{t+1}$的条件分布，仅仅与其前一个状态$i_t$有关，即:
$$p(i_{t+1}|i_1,i_2,...,i_t)=p(i_{t+1}|i_t)$$

隐马尔可夫模型是由马尔可夫链生成随机不可观测的随机状态序列，再由各个状态生成可观测的随机序列：

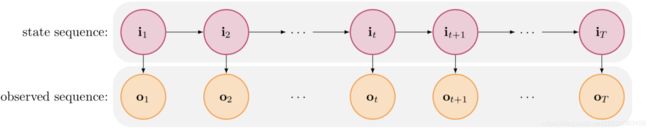
可以得到上述隐马尔可夫模型的图模型结构，状态序列(不可观测的)为$I=i_1,i_2,...,i_T$，观测序列为$O=o_1,o_2,...,o_T$

根据上述图，去理解HMM的两个基本假设.

HMM模型的两个基本的假设

齐次马尔可夫假设：假设隐藏的马尔可夫链在任一时刻t的状态只依赖于其前一个时刻的状态：
$$p(i_t|i_{t-1},o_{t-1},...,i_1,o_1)=p(i_t|i_{t-1}),i=1,2,...,T$$
上式中的$i_t$表示$t$时刻的状态序列值，$o_t$表示$t$时刻的观测序列值，再强调一遍：该假设就是在说当前时刻序列状态只依赖于上一时刻序列状态。

观测独立性假设：假设任意时刻的观测状态$o_t$只依赖于该时刻的马尔可夫链$i_t$ 的状态，与其他的观测状态及状态都无关。

继续上边的符号表达：
$$p(o_t|i_T,o_T,i_{T-1},o_{T-1},...,i_{t+1},o_{t+1},....,i_1,o_1)=p(o_t|i_t)$$

生成模型 or 判别模型

1.生成模型：

由生成方法学习到的模型称之为生成模型，生成方法是由数据学习联合分布$P(X,Y)$，然后求出条件概率分布$P(Y|X)$作为预测的模型：
$$P(Y|X)=\frac{P(X,Y)}{P(X)}$$
典型的生成模型有：朴素贝叶斯法，隐马尔可夫模型，生成对抗网络（GAN），变分自编码器（VAE）；

生成模式有两种：确定性和非确定性的。

确定性生成模式：变化规律固定，能够根据当前状态，确定判断出下一状态，如交通红绿灯的变化；

非确定性生成模式：变化相对多样，不能准确确定下一状态，如天气的变化。

2.判别模型：

由判别方法学习到的模型称之为判别模型，判别方法是由数据直接学习决策函数或者条件概率分布$P(Y|X)$作为预测的模型。

典型的判别模型有：$k$近邻法，感知机模型，决策树，逻辑回归模型，最大熵模型，支持向量机，提升方法和条件随机场等。

隐藏的马尔可夫链/观测序列

一个比较好的例子去介绍HMM模型，可以参考一下：

http://www.360doc.com/content/13/0226/14/11619026_268005483.shtml

Wikipedia 介绍： https://en.wikipedia.org/wiki/Hidden_Markov_model

简单描述一下这个例子：

假设A与B是两个处于不同地方的朋友，A关心B每天干了什么事情（观测序列）「散步，购物，大扫除」，想要通过B干的事情去推断出B处地的天气变化(隐藏序列)「晴天，雨天」

隐藏序列集合：$S_{hidden}=\{晴天，雨天\}$

观测序列集合：$S_{observations}=\{散步，购物，大扫除\}$

初始状态概率矩阵：

$M_{start\_probability}=\{雨天:0.6,晴天:0.4\}$

状态转移矩阵：

$$M_{transition\_probability}=\{雨天:\{晴天：0.3，雨天：0.7\},晴天:\{晴天：0.6，雨天：0.4\}\}$$

发射概率矩阵：

$M_{emission\_probability}=\{雨天:\{散步：0.1，购物：0.4，大扫除：0.5\},晴天:\{散步：0.6，购物：0.3，大扫除：0.1\}\}$

隐藏序列：表示无法直接观测到的状态，就上述例子而言就是对方的天气状态；

观测序列：可以直接观测到的状态，就上述例子而言就是获取到的B执行的事情；

初始状态概率矩阵：表示B第一次告诉A的时候，得到的隐藏状态集合中每个状态发生的概率；

状态转移矩阵：表示从一个状态到另一个状态变化的概率，如在上述例子中，从雨天到晴天的概率为0.3；

发射状态矩阵：表示B在相应隐藏状态（天气）下，去执行得到观测状态（执行的动作）的概率，如在雨天，B去散步的概率为0.1；

HMM模型综上描述起来就是五个要素：

两个序列：隐藏序列和观测序列

三个矩阵：初始状态矩阵，发射状态矩阵以及状态转移矩阵

隐马尔可夫模型的3个基本问题

概率计算问题：给定模型和观测序列，计算观测序列出现的概率$P(O|\lambda )$;

学习问题：已知观测序列求解模型参数，使得模型在观测序列下的概率最大$P(O|\lambda )$，最大似然估计求参数；

预测问题：给定观测序列，求有可能的对应的状态序列$I$

符号说明（借鉴《统计学习方法》–李航）：

$Q:$所有可能的状态集合， $Q=\{q_1,q_2,...,q_N\}$

$V$: 所有可能的观测状态的集合，$V=\{v_1,v_2,...,v_M\}$

$O$: 实际观测序列，$O=\{o_1,o_2,...,o_T\}$

$I$: 隐藏的状态序列，$I=\{i_1,i_2,...,i_T\}$

$A$: 状态转移矩阵，$a_{ij}$表示$t$时刻处于状态$q_i$在$t+1$时刻转移到$q_j$的概率

$B$: 观测概率矩阵，$b_{j{o}_t}$表示$t$时刻处于状态$q_j$条件下生成观测$o_t$的概率

$\pi$： 初始状态概率向量，猜猜这个向量的长度为多少？当然是等于所有可能的状态集合啦～～～

根据上式定义，有:

1. 所有的初始状态概率和为1:
   $$\sum _{i=1}^N{\pi }_i=1$$

2. 时刻$t$转移到一下个所有可能的状态的概率和为1:

$$\sum _{j=1}^N{a}_{ij}=1$$

3. 时刻$t$，由状态$j$观测到的所有可能的观测值的概率和为1:

$$\sum _{k=1}^M{b}_{jk}=1$$

第一个问题：概率计算问题--计算观测序列出现的概率

概率计算问题描述：给定模型$\lambda =(A,B,\pi )$和观测序列$O=(o_1,o_2,...,o_T)$，计算观测序列出现的概率$P(O|\lambda )$.

1.直接法

直接法，就是直接按照概率公式进行计算，通过穷举出所有可能的长度为$T$的状态序列和观测序列的联合概率，然后对状态序列求和：
$$P(O|\lambda )=\sum _{I}P(O,I|\lambda )=\sum _{I}P(O|I,\lambda )P(I|\lambda )$$
根据隐马尔可夫模型的定义，可以计算状态序列$I=(i_1,i_2,...,i_T)$的概率（齐次马尔可夫性假设）：
$$P(i_1,i_2,...,i_T|\lambda )={\pi }_{i_1}{a}_{i_1{i}_2}{a}_{i_2{i}_3}...a_{i_{T-1}{i}_T}$$
计算观测序列$O=(o_1,o_2,...,o_T)$的概率（观测独立性假设）：
$$P(o_1,o_2,...,o_T|I,\lambda )=b_{i_1{o}_1}{b}_{i_2{o}_2}...b_{i_T{o}_T}$$

得到他们的联合概率分布如下：
$$\begin{array}{rl}P(O,I|\lambda )& =P(O|I,\lambda )P(I|\lambda )=b_{i_1{o}_1}{b}_{i_2{o}_2}...b_{i_T{o}_T}{\pi }_{i_1}{a}_{i_1{i}_2}{a}_{i_2{i}_3}...a_{i_{T-1}{i}_T}\end{array}$$
对状态序列求和：
$$\begin{array}{rl}P(O|\lambda )& =\sum _{I}P(O,I|\lambda )=\sum _I{b}_{i_1{o}_1}{b}_{i_2{o}_2}...b_{i_T{o}_T}{\pi }_{i_1}{a}_{i_1{i}_2}{a}_{i_2{i}_3}...a_{i_{T-1}{i}_T}\end{array}$$

分析一下时间复杂度，对于状态序列$I=(i_1,i_2,...,i_T)$， $i_1,i_2,...,i_T$均有$N$种可能的选择，所以共有$N^T$中方法，加之求和符号，所以直接法总的复杂度为$O(T{N}^T)$，指数级别的时间复杂度，往往是不可取的。

2.前向算法—动态规划的思想

前向算法的核心：定义前向概率
$${\alpha }_t(i)=p(o_1,o_2,...,o_t,i_t=q_i|\lambda )$$

根据定义的公式，简单理解就是为从图红线处断隔开，只考虑前半部分计算前向概率，注意：前向概率定义没有包括对隐状态$i_1,i_2,...,i_{t-1}$的定义。

如此定义的原因是希望后边能够构建动态规划的递推公式：

根据上述定义:

(1) 计算$t=1$时刻定义的前向概率：
$${\alpha }_1(i)=p(o_1,i_1=q_1|\lambda )=p(o_1|i_1,\lambda )p(i_1|\lambda )=b_{i_1{o}_1}{\pi }_i，i=1,2,...,N$$
(2) 构建递推公式（不知道推的过程我是不是复杂化了），对$t=1,2,...,T-1$有：
$$\begin{array}{rl}{\alpha }_{t+1}(i)& =p(o_1,o_2,...,o_t,o_{t+1},i_{t+1}=q_i|\lambda )\\ & =\sum _{j=1}^{N}p(o_1,o_2,...,o_t,o_{t+1},i_{t+1}=q_i,i_t=q_j|\lambda )(1)-期望\\ & =\sum _{j=1}^{N}p(o_1,o_2,...,o_t,i_t=q_j|o_{t+1},i_{t+1}=q_i,\lambda )p(o_{t+1},i_{t+1}=q_i|\lambda )(2)-贝叶斯公式\\ & =\sum _{j=1}^{N}p(o_1,o_2,...,o_t,i_t=q_j|i_{t+1}=q_i,\lambda )p(o_{t+1}|i_{t+1}=q_i,\lambda )p(i_{t+1}=q_i|\lambda )(3)-贝叶斯公式\\ & =\sum _{j=1}^{N}p(o_1,o_2,...,o_t,i_t=q_j,i_{t+1}=q_i,\lambda )p(o_{t+1}|i_{t+1}=q_i,\lambda )(4)-贝叶斯公式\\ & =\sum _{j=1}^{N}p(o_1,o_2,...,o_t,i_{t+1}=q_i|i_t=q_j,\lambda )p(i_t=q_j|\lambda )p(o_{t+1}|i_{t+1}=q_i,\lambda )(5)-贝叶斯公式\\ & =\sum _{j=1}^{N}p(o_1,o_2,...,o_t|i_t=q_j,\lambda )p(i_t=q_j|\lambda )p(i_{t+1}=q_i|i_i=q_j)p(o_{t+1}|i_{t+1}=q_i,\lambda )\\ & (6)-贝叶斯公式+隐马尔可夫假设\\ & =\sum _{j=1}^{N}p(o_1,o_2,...,o_t,i_t=q_j|\lambda )p(i_{t+1}=q_i|i_i=q_j)p(o_{t+1}|i_{t+1}=q_i,\lambda )(7)-贝叶斯公式\\ & =\sum _{j=1}^N{\alpha }_t(j)a_{ji}{b}_{i{o}_{t+1}},i=1,2,3,...,N\end{array}$$
(3) 递推终止之后：
$$P(O|\lambda )=\sum _{i}P(O,i_t=q_i|\lambda )=\sum _{i=1}^N{\alpha }_T(i)$$
此时来计算一下时间复杂度：

${\alpha }_1(i)$中的$i$有N种可能性，${\alpha }_{t+1}(i)$中的计算结果都依赖于${\alpha }_t(j)$对N个状态求和的结果（直接引用，避免了重复计算），每次递推都是在前一次的基础上做的，累加$O(T)$次，所以总的时间复杂度为$O(N^{2}T)$，从指数级别的复杂度降成了多项式级别的复杂度.

3.后向算法—动态规划的思想

后向算法的核心：定义后向概率(时刻$t$的状态为$q_i$的条件下，$t+1$到$T$的部分观测序列为$o_{t+1},o_{t+2},...,o_T$的概率)
$${\beta }_t(i)=p(o_{t+1},o_{t+2},...,o_T|i_t=q_i,\lambda )$$

根据上述后向概率的定义：

（1）计算$t=T$时刻的后向概率：
$${\beta }_T(i)=1,i=1,2,...,T$$
（2）构建递推公式，递推$t=T-1,T-2,...,1$
$$\begin{array}{rl}{\beta }_t(i)& =p(o_{t+1},o_{t+2},...,o_T|i_t=q_i,\lambda )\\ & =\sum _{j}p(o_{t+1},o_{t+2},...,o_T,i_{t+1}=q_j|i_t=q_i,\lambda )\\ & =\sum _{j}p(o_{t+1},o_{t+2},...,o_T|i_t=q_i,i_{t+1}=q_j\lambda )p(i_{t+1}=q_j|i_t=q_i,\lambda )\\ & =\sum _{j}p(o_{t+1},o_{t+2},...,o_T|i_t=q_i,i_{t+1}=q_j\lambda )a_{ij}\\ & =\sum _{j}p(o_{t+2},...,o_T|i_{t+1}=q_j,\lambda )p(o_{t+1}|i_t=q_i,i_{t+1}=q_j,\lambda )a_{ij}\\ & =\sum _j{\beta }_{t+1}(j)b_{j{o}_{t+1}}{a}_{ij},i=1,2,...,N\end{array}$$
（3）计算观测序列的概率：
$$\begin{array}{rl}P(O|\lambda )& =\sum _{i=1}^{N}P(O,i_1=q_i|\lambda )=\sum _{i=1}^{N}P(O|i_1=q_i,\lambda )p(i_1=q_i|\lambda )=\sum _{i=1}^N{\beta }_1(i){\pi }_i{b}_{i{o}_1}\end{array}$$

同前向算法分析复杂度原理可知，后向算法时间复杂度也为$O(N^{2}T)$

第二个问题：学习问题--计算模型的参数

学习问题包括两种：

• 给定观测序列和状态序列的学习问题–监督学习；

• 只给定观测序列的学习问题–非监督学习，Baum-Welch算法。

1. 给定观测序列和状态序列–监督学习

依据大数定理，计算频率近似于概率（此处不详细描述，具体可参见《统计学习方法》-李航）

2. 只给定观测序列–非监督学习，Baum-Welch算法

只给定观测序列的学习问题，主要是指给定观测序列$O=(o_1,o_2,...,o_t)$的情况下，学习模型的参数：$\lambda =(A,B,\pi )$，在状态序列未知的情况下，其实就是含有隐变量的模型参数求解问题，利用最大似然估计求解：
$$P(O|\lambda )=\sum _{I}P(O|I,\lambda )P(I|\lambda )$$
给定观测序列，状态序列未知，熟悉EM算法的应该很容易联想到这个算法了，可以将状态序列看作是EM算法中的隐变量，回顾一下EM算法的求解步骤：
$$\begin{array}{rl}& E-step:Q(\theta ,{\theta }^{(i)})=\sum _{z}logP(x,z,\theta )P(z|x,{\theta }^{(i)})\\ & M-step:{\theta }^{(i+1)}:=argma{x}_{\theta }Q(\theta ,{\theta }^{(i)})\end{array}$$
其中$z^{(i)}$表示隐变量，$x$表示输入数据，$\theta$表示模型求解的参数

继续回到Baum-Welch算法：

(1) 目标对数似然函数：$P(O,I|\lambda )$;

(2) 利用EM算法求解：

• E步骤，求解Q函数：
  $$\begin{array}{rl}Q(\lambda ,\tilde{\lambda })& =\sum _{I}logP(O,I|\lambda )p(I|\tilde{\lambda })=\sum _{I}logP(O,I|\lambda )\frac{P(O,I|\tilde{\lambda })}{P(O|\tilde{\lambda })}\propto \sum _{I}logP(O,I|\lambda )P(O,I|\tilde{\lambda })\end{array}$$
  其中$\tilde{\lambda }$是隐马尔可夫模型参数的当前估计值，$\lambda$是要极大化的模型参数。

  根据直接计算（直接法）联合概率的公式：
  $$\begin{array}{r}P(O,I|\lambda )={\pi }_i{a}_{i_1{i}_2}{a}_{i_2{i}_3}...a_{i_{T-1}{i}_T}{b}_{i_1{o}_1}{b}_{i_2{o}_2}...b_{i_T{o}_T}\end{array}$$
  取对数函数：
  $$\begin{array}{rl}logP(O,I|\lambda )& =log({\pi }_i{a}_{i_1{i}_2}{a}_{i_2{i}_3}...a_{i_{T-1}{i}_T}{b}_{i_1{o}_1}{b}_{i_2{o}_2}...b_{i_T{o}_T})\\ & =log{\pi }_i+\sum _{t=1}^{T-1}log{a}_{i_t{i}_{t+1}}+\sum _{t=1}^{T}log{b}_{i_t{o}_t}\end{array}$$
  带入Q函数：
  $$\begin{array}{rl}\sum _{I}logP(O,I|\lambda )P(O,I|\tilde{\lambda })& =\sum _{I}log({\pi }_i{a}_{i_1{i}_2}{a}_{i_2{i}_3}...a_{i_{T-1}{i}_T}{b}_{i_1{o}_1}{b}_{i_2{o}_2}...b_{i_T{o}_T})P(O,I|\tilde{\lambda })\\ & =\sum _I(log{\pi }_i+\sum _{t=1}^{T-1}log{a}_{i_t{i}_{t+1}}+\sum _{t=1}^{T}log{b}_{i_t{o}_t})P(O,I|\tilde{\lambda })\end{array}$$

• M-step 求解模型的参数

  上述三个加和拆开，得到三个部分，三个部分分别满足约束条件：${\sum }_i{p}_i=1,{\sum }_j{a}_{i}j=1,{\sum }_k{b}_{j}k=1$，分别对这三个部分依次利用拉格朗日求解，即可求解得到模型的参数。

第三个问题：预测问题--给定观测序列预测隐藏序列

预测算法–（经典算法–维特比算法）-- 参照《统计学习方法》

维特比算法实际是用动态规划解马尔可夫模型预测问题，用动态规划求解概率最大的路径。


定义$t$时刻状态为$i$的所有单个路径$(i_1^{\ast },i_2^{\ast },...,i_t^{\ast })$中概率最大值：
$${\delta }_t(i)=ma{x}_{i_1,i_2,...,i_{t-1}}P(i_t=i,i_{t-1},...,i_1,o_t,o_{t-1},...,o_1|\lambda ),i=1,2,...,N$$
由定义和隐马尔可夫假设可以得到变量$\delta$的递推公式，可以推出如下公式：
$$\begin{array}{rl}{\delta }_{t+1}(i)& =ma{x}_{i_1,i_2,...,i_t}P(i_{t+1}=i,i_t,...,i_1,o_{t+1},o_t,o_{t-1},...,o_1|\lambda )\\ & =ma{x}_{1\le j\le N}[{\delta }_t(j)a_{ji}]b_{i{o}_{t+1}},i=1,2,...,N;t=1,2,...,T-1\end{array}$$
定义在时刻$t$状态为$i$的所有单个路径$(i_1,i_2,...,i_t)$中概率最大的路径的第$t-1$个结点为：
$${\varphi }_t(i)=argma{x}_{1\le j\le N}[{\delta }_{t-1}(j)a_{ji}],i=1,2,...,N$$

维特比算法：

（1） 初始值： ${\delta }_1(i)={\pi }_i{b}_{i{o}_1}，i=1,2,...,N;$ ${\varphi }_1(i)=0,i=1,2,...,N$

（2）递推：对$t=2,3,4,...,T$，有：
$$\begin{gathered} {\delta }_t(i)=ma{x}_{1\le j\le N}[{\delta }_{t-1}(j)a_{ji}]b_{i{o}_t},i=1,2,...,N; \\ {\varphi }_t(i)=argma{x}_{1\le j\le N}[{\delta }_{t-1}(j)a_{ji}],i=1,2,...,N \end{gathered}$$
（3）终止：
$$\begin{gathered} P^{\ast }=ma{x}_{1\le i\le N}{\delta }_T(i); \\ {i}_T^{\ast }=argma{x}_{1\le i\le N}[{\delta }_T(i)] \end{gathered}$$
（4）最优路径回溯：对$t=T-1,T-2,...,1$，有：
$$i_t^{\ast }={\varphi }_{t+1}(i_{t+1}^{\ast })$$
最优路径为：$I^{\ast }=(i_1^{\ast },i_2^{\ast },...,i_T^{\ast })$

整个算法的流程如上述描述，下边简单介绍一下每一步都在干什么？

（1）定义初始值，针对第一个节点而言，其概率值即为每个状态的概率值乘以每个状态下观测到第一个值的概率，即${\pi }_i{b}_{i{o}_1}$;

（2）在初始值给定的条件下，计算产生第二个观测序列值在每一个状态下的概率最大值，即${\delta }_2(i)$，使用${\varphi }_2(i)$来记录到达该最大概率值的上一个状态，依次递推下去。这里${\delta }_t(i)$获取的是概率最大值，${\varphi }_t(i)$获取的是到达概率最大值的上一个状态；

（3）最终计算到最后一个时刻$T$的最大概率值，并且可以进行最优路径的回溯。

参考资料：

[1] http://www.360doc.com/content/13/0226/14/11619026_268005483.shtml

[2] https://en.wikipedia.org/wiki/Hidden_Markov_model

[3] 统计学习方法，李航著，清华大学出版社