你所不知道的按位运算

本文转载来之微信公众号编程派

https://mp.weixin.qq.com/s?__biz=MzAwNDc0MTUxMw==&mid=2649639595&idx=1&sn=3b214b17551706e5dd9b484e2d33f3fc&chksm=833daa4db44a235bc0e2f4087c3dc4df09c0ceaad62ff8498d36c8a2262b6dd5d8060cf4dcc9&scene=0&key=c50f8b988e61749a3443cec973119b3b7f52030a51389e4aa9251b84bfc6728f07f9d333af2504d114307fbf8f443a71&ascene=0&uin=MjA1NDAwNzE4MA%3D%3D&devicetype=Windows+10&version=61050021&pass_ticket=cBDJc2up%2FirRSJyuW7ZJ8DOsmH14RqmCZ%2BR4MXFIMZbJzN7ackBAuhXSmdF4S86q

先来看LeetCode上的Divide Two Integers题目要求：

Divide two integers without using multiplication, division and mod operator.

就是说不用乘法，除法，求模运算来实现两个整数相除，看起来很简单，我可以用除数减去被除数，直到除数小于被除数，记录减法操作的次数即可。假设是计算m/n，那么时间复杂度为O(m/n)。用Python实现后，TimeLimit Exceeded。我们考虑有没有更加优化的算法呢？

如果很难想得到，那就先来回忆下二进制数按位运算的一些知识。

二进制数按位运算

计算机里面所有数据都存储为0，1串，所有的运算归根到底都转为二进制数的运算。相信大家都知道二进制数按位运算的规则：

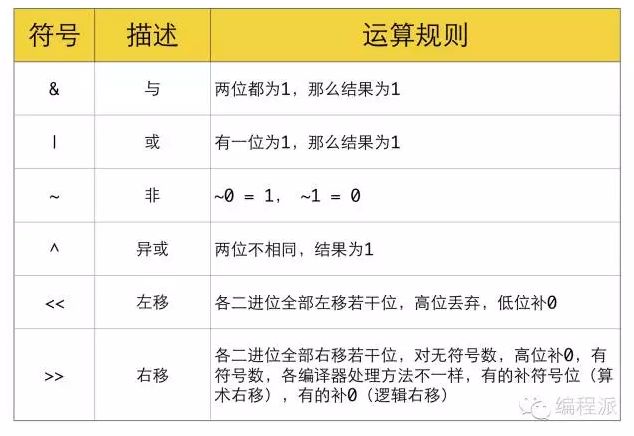
来看一些简单的例子：

[code]

1010 & 1100 = 1000

1010 | 1100 = 1110

1010 ^ 1100 = 0110

1010 << 2   = 101000

1010 >> 2   = 10

~1010       = 0101

[/code]

单纯的二进制位之间的这些运算相当简单，但对我们实际编程并没有直接帮助，因为编程过程中需要的经常是数字间的运算，比如 5*(2^4)。真的是这样吗？接着往下看！

计算机中数字的存储方式

我们都知道计算机中万物皆为0、1，将万物变为0、1的过程叫做编码，这里我们只讨论将数字编码为0、1的过程。

计算机中对数字的表示有三种方式：原码，反码，补码：

• 原码表示法在数值前面增加了一位符号位（即最高位为符号位）：正数该位为0，负数该位为1。比如十进制3如果用8个二进制位来表示就是 00000011， -3就是 10000011。

• 反码表示方法：正数的反码是其本身；负数的反码是在其原码的基础上，符号位不变，其余各个位取反。

• 补码表示方法：正数的补码是其本身；负数的补码是在其原码的基础上，符号位不变，其余各位取反，最后+1。 (即在反码的基础上+1)

原码容易被人脑直接识别并用于计算，但是对于计算机来说并不友好。所以在计算机系统中，数值一律用补码来表示、运算和存储。使用补码，可以将符号位和数值域统一处理，将加法和减法统一处理。此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。详细的解释可以参考原码,反码,补码详解。

数字的按位运算

计算机中数字存储为补码形式，各个数之间的运算也是对它们的补码做运算，而且得到的结果也是补码，如下图：

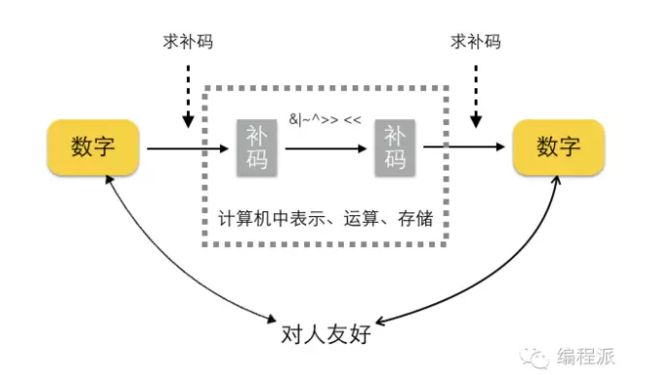
各种编程语言都提供了对补码的二进制位直接进行运算的方法。以Python为例：

[code]

>>> 0b1010 & 0b1100

8   #1000

>>> 0b1010 | 0b1100

14  #1110

>>> 0b1010 ^ 0b1100

6   #0110

>>> 0b1010 << 2

40  #101000

>>> 0b1010 >> 2

2   #10

>>> ~0b1010

-11 #10000000 00000000 00000000 00001011

>>> type(0b1010)

[/code]

上面0b开头的0、1串表示整型数字，在32位操作系统中，Python中int类型一般占32个二进制位，以最后一个求反运算为例子，1010的补码为

00000000 00000000 00000000 00001010

求反操作后为：

11111111 11111111 11111111 11110101

即为-11(原码为：10000000 00000000 00000000 00001011)的补码。（对一个数的补码求补码即可得到该数的原码）

另辟蹊径的按位运算

那么按位运算在实际编程中可以扮演哪些角色呢？简单点地，可以用来判断奇、偶数：num & 0x1，或者对一个数变换符号：~num + 1；复杂点的可以用来交换两个数，求绝对值等等。

1、不用额外的变量实现两个数字互换。

[code]

def swap(num_1, num_2):

    num_1 ^= num_2

    num_2 ^= num_1

    num_1 ^= num_2

    return num_1, num_2

[/code]

证明很简单，我们只需要明白异或运算满足下面规律：

• 0^a = a;

• a^a = 0;

• a^b^c = a^c^b;

巧妙运用异或可以高效解决很多问题，比如
找出数组中只出现了一次的数（除了一个数只出现一次外，其他数都是出现两次），以及它的升级版：数组中只出现1次的两个数字(百度面试题)。

2、不用判断语句来实现求绝对值。

[code]

def bit_abs(num):

    negative = num >> 31

    return (num ^ negative) - negative

[/code]

这里假设程序运行环境中操作系统为32位，int型整数(不考虑整数溢出)用32位存储，因此可以用 num>>31取出符号位，后面的部分留给大伙证明。

3、 生成一个集合的所有子集合。

比如说我们有一个集合{2,3,4}，那么它的子集合即为{}, {2}, {3}, {4}, {2,3}, {2,4},{3,4}, {2,3,4}，一共有2 ** 3 = 8个。如何用程序生成所有的子集合呢？用位操作来做的话就相当简单，只需要将0到7中的每个数字转为二进制，如果第i位为0，则表示子集中不包含有原集中第i位；如果为1，则包含第i位，如下：

[code]

nums = [1, 2, 3]

subsets = []

n = len(nums)

sum_sets = 2 ** n

for i in range(sum_sets):

    cur_set = []

    for j in range(n):

        power = 2 ** j

        if i & power == power:

            cur_set.append(nums[j])

    subsets.append(cur_set)

print subsets

[/code]

Leetcode 题目思路

回到文章开始提到的题目中，我们对除数减去被除数的过程稍作改进。假设求m/n，我们不一次次的 m-n，而是找到n的一个倍数，使得m-x*n尽可能小，这样能减少循环减法的次数，进而提高效率。我们知道在按位操作中，n << k 相当于 n * 2^k ，因此可以用2^k来找合适的x。

我们需要这样的一个数字k，它使得n * 2^k < m < n * 2^(k+1) ， 然后用 m - n *2^k，得到新的m’。再找相应的k’，做减法，如此循环即可。代码放在这里。其实LeetCode上面有许多题目都可以用位操作的思想去解决。