原型聚类（一）k均值算法和python实现

原型聚类

原型聚类算法假设聚类结构能通过一组原型刻画，在现实聚类任务中极为常用。通常情形下，算法先对原型进行初始化，然后对原型进行迭代更新求解。这里的“原型”我认为实际上就是“原来的模型”，这类算法企图模拟出生成数据集的模型。

k均值算法（k-means)

若存在一个样本集$D=\left\{\begin{array}{c}{x}_1,x_2,...,x_m\end{array}\right\}$,k均值算法要求给出类别个数“k”，我们需要将这个样本集D中的样本划分到类别集合$C=\left\{\begin{array}{c}{C}_1,C_2,...,C_k\end{array}\right\}$中，目的是最小化平方误差：
$$E=\sum _{i=1}^k\sum _{x\in C_i}{\Vert x-{\mu }_i\Vert }_2^2$$
其中${\mu }_i=\frac{1}{|C_i|}{\sum }_{x\in C_i}x$ 是簇$C_i$的均值向量，E越小，说明簇内样本相似度越高，聚类效果越好。

最小化E是一个NP难问题（NP是指非确定性多项式（non-deterministic polynomial，缩写NP）），因此k均值算法采用贪心策略，通过不断迭代来近似求解上式

（图片来自《机器学习》周志华）
上面的伪代码中对于初始$\mu$的选取是随机的，这导致了算法的不稳定，本人实现的k-means算法的初值是选择k个相对距离最远的样本点作为初始$\mu$。

算法缺点：

1. k值由用户确定，不同的k值会获得不同的结果
2. 对初始簇中心的选择敏感
3. 不适合发现非凸形状的簇或大小差别较大的簇
4. 特殊值（离群值）对模型的影响较大

算法优点：

1. 容易理解，聚类效果不错
2. 处理大数据集时，算法可以保证较好的伸缩性（在处理各种规模的数据时都有很好的性能。随着数据的增大，效率不会下降很快）和高效率
3. 当簇近似高斯分布时，分类效果很好

python3.6实现：

# -*- coding: gbk -*-

import numpy as np
from sklearn.datasets import make_moons
from sklearn.datasets.samples_generator import make_blobs
import matplotlib.pyplot as plt
from collections import Counter
import copy


class KMeans():
    def __init__(self, k=3, max_iter=300):
        self.k = k
        self.max_iter = max_iter

    def dist(self, x1, x2):
        return np.linalg.norm(x1 - x2)

    def get_label(self, x):
        min_dist_with_mu = 999999
        label = -1

        for i in range(self.mus_array.shape[0]):
            dist_with_mu = self.dist(self.mus_array[i], x)
            if min_dist_with_mu > dist_with_mu:
                min_dist_with_mu = dist_with_mu
                label = i

        return label

    def get_mu(self, X):
        index = np.random.choice(X.shape[0], 1, replace=False)
        mus = []
        mus.append(X[index])
        for _ in range(self.k - 1):
            max_dist_index = 0
            max_distance = 0
            for j in range(X.shape[0]):
                min_dist_with_mu = 999999

                for mu in mus:
                    dist_with_mu = self.dist(mu, X[j])
                    if min_dist_with_mu > dist_with_mu:
                        min_dist_with_mu = dist_with_mu

                if max_distance < min_dist_with_mu:
                    max_distance = min_dist_with_mu
                    max_dist_index = j
            mus.append(X[max_dist_index])

        mus_array = np.array([])
        for i in range(self.k):
            if i == 0:
                mus_array = mus[i]
            else:
                mus[i] = mus[i].reshape(mus[0].shape)
                mus_array = np.append(mus_array, mus[i], axis=0)

        return mus_array

    def init_mus(self):
        for i in range(self.mus_array.shape[0]):
            self.mus_array[i] = np.array([0] * self.mus_array.shape[1])

    def fit(self, X):
        self.mus_array = self.get_mu(X)
        iter = 0

        while(iter < self.max_iter):

            old_mus_array = copy.deepcopy(self.mus_array)

            Y = []
            # 将X归类
            for i in range(X.shape[0]):
                y = self.get_label(X[i])
                Y.append(y)

            self.init_mus()
            # 将同类的X累加
            for i in range(len(Y)):
                self.mus_array[Y[i]] += X[i]

            count = Counter(Y)
            # 计算新的mu
            for i in range(self.k):
                self.mus_array[i] = self.mus_array[i] / count[i]

            diff = 0
            for i in range(self.mus_array.shape[0]):
                diff += np.linalg.norm(self.mus_array[i] - old_mus_array[i])
            if diff == 0:
                break
            iter += 1

        self.E = 0
        for i in range(X.shape[0]):
            self.E += self.dist(X[i], self.mus_array[Y[i]])
        print('E = {}'.format(self.E))
        return np.array(Y)


if __name__ == '__main__':

    fig = plt.figure(1)

    plt.subplot(221)
    center = [[1, 1], [-1, -1], [1, -1]]
    cluster_std = 0.35
    X1, Y1 = make_blobs(n_samples=1000, centers=center,
                        n_features=3, cluster_std=cluster_std, random_state=1)
    plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1)

    plt.subplot(222)
    km1 = KMeans(k=3)
    km_Y1 = km1.fit(X1)
    mus = km1.mus_array
    plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=km_Y1)
    plt.scatter(mus[:, 0], mus[:, 1], marker='^', c='r')

    plt.subplot(223)
    X2, Y2 = make_moons(n_samples=1000, noise=0.1)
    plt.scatter(X2[:, 0], X2[:, 1], marker='o', c=Y2)

    plt.subplot(224)
    km2 = KMeans(k=2)
    km_Y2 = km2.fit(X2)
    mus = km2.mus_array
    plt.scatter(X2[:, 0], X2[:, 1], marker='o', c=km_Y2)
    plt.scatter(mus[:, 0], mus[:, 1], marker='^', c='r')
    plt.show()

运行分类图片如下：

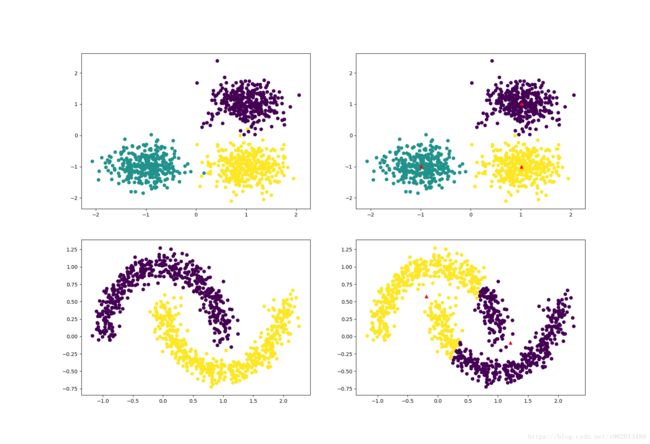
图中左侧为原始生成的数据，右边为k-means聚类效果，红色三角为最终的均值向量

参考

《机器学习》周志华
https://blog.csdn.net/intelligence1994/article/details/69574080