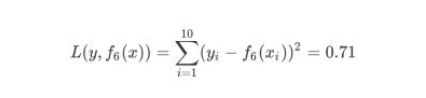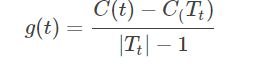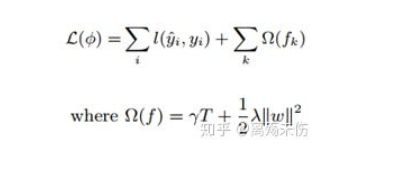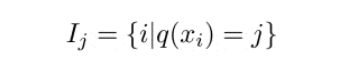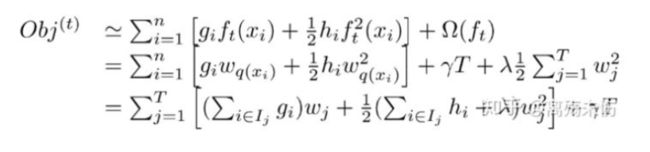Xgboost算法梳理

算法分类与回归树的英文是Classfication And Regression Tree，缩写为CART。CART算法采用二分递归分割的技术将当前样本集分为两个子样本集，使得生成的每个非叶子节点都有两个分支。非叶子节点的特征取值为True和False，左分支取值为True，右分支取值为False，因此CART算法生成的决策树是结构简洁的二叉树。CART可以处理连续型变量和离散型变量，利用训练数据递归的划分特征空间进行建树，用验证数据进行剪枝。

• 如果待预测分类是离散型数据，则CART生成分类决策树。

• 如果待预测分类是连续性数据，则CART生成回归决策树。

CART分类树

 

• 分类树预测的都是离散型数据，通过比较分裂前后gini系数大小来选择最佳分裂点

 

• 基尼系数越大，样本集合的不确定性越大

• 我们选择基尼系数最小的作为最佳分裂点

 

CART回归树，

• CART回归树预测回归连续型数据，可以用平方误差来表示回归树对于训练数据的预测方法，用平方误差最小的准则求解每个单元上的最优输出值。

            

            步骤：

                    1.选定每个切分点，博主的例子是1-10中，每隔0.5选一个切分点，那切分点集合就为【1.5,2.5，...9.5】共9个切分点

                     2.套用分割点公司，计算平方误差

 

                        3.此时计算出x=6.5时候，平方误差最小，得到第一课回归树

                            

                       4.这个时候还没完，只是第一步迭代，接下来我，嗯要根据得到的回归树，更新数据集，得到残差

                    5.按照第一颗回归树的方法来得到第二颗，第三棵树。。。。

                        6. 用f6(x)拟合训练数据的平方损失误差如下所示，假设此时已经满足误差要求，那么f(x)=f6(x)便是所求的回归树。

                                                

 

 

CART剪枝

一颗充分生长的树成为完全树，T0，我们一方面需要剪掉一些树枝来防止过拟合，但同时剪得枝可能是一些有用的特征，造成预测的误差增大，那我们还如何去平衡这两个点呢？

 

   

CART剪枝包括两部分，剪枝获得子树序列，对子树序列进行交叉验证，选择最优子树。

  

• 我们可以这么理解，分母是叶子结点较少的数量，分子是误差减小的数量，比值是误差减小率，如果误差减小率很小，那么还不如不剪枝呢。

• 在计算整体的损失函数时，这个内部节点以外的值都没变，只有这个内部节点的局部损失函数改变了，因此我们本需要计算全局的损失函数，但现在只需要计算内部节点剪枝前和剪枝后的损失函数。

我的思考：

这里要理清一个概念，因为我们优化的终极目标是使节点尽量少，所以我就逆向去思考，首先从单根节点开始去增加节点，看看增加节点有没有使误差减少，如无必要勿增实体。如果花很大功夫增加节点，并没有使误差减少很多，那我们干脆就不增加这个节点。

1.g(t)代表每个叶子节点带来的误差减小量，如果g(t)越小，也就是增加叶子带来的误差减小量越小，也就是增加这个叶子节点的作用越小，花那么大的功夫增加叶子节点，误差才减小那么一点点，还不如不要因此优先剪去g(t)最小的T

 

xgboost算法原理知识

3.1 定义树的复杂度

把树拆分成结构部分q和叶子权重部分w。

树的复杂度函数和样例：

 

定义树的结构和复杂度的原因很简单，这样就可以衡量模型的复杂度了啊，从而可以有效控制过拟合。

 

和传统的boosting tree模型一样，xgboost的提升模型也是采用的残差（或梯度负方向），不同的是分裂结点选取的时候不一定是最小平方损失。

损失函数

最终的目标函数只依赖于每个数据点的在误差函数上的一阶导数和二阶导数。这么写的原因很明显，由于之前的目标函数求最优解的过程中只对平方损失函数时候方便求，对于其他的损失函数变得很复杂，通过二阶泰勒展开式的变换，这样求解其他损失函数变得可行了。很赞！

 

当定义了分裂候选集合的时候，可以进一步改目标函数。分裂结点的候选响集是很关键的一步，这是xgboost速度快的保证，怎么选出来这个集合，后面会介绍。

    

求解

分裂结点算法

3.1 基础精确的贪心算法

方程（7）的关键问题是找到合适的分割，精确的贪心算法通过列举所有特征的可能划分找到最优划分解，许多单机Tree算法使用这种方式找到划分点，例如 sklearn、Rs gbm、单机的XGBoost。精确的算法需要排序成连续的特征，之后计算每个可能划分的梯度统计值，如算法1：

 

3.2 近似算法

精确通过列举特征所有可能的划分，耗时，当数据量大的时候，几乎不可能将数据全部加载进内存，精确划分在分布式中也会有问题。我们总结了近似的策略，如算法二所示，算法首先根据特征分布的百分比提议候选划分点，之后按照候选划分点将特征映射到槽中，找到最好的划分百分点。全局划分需要尽可能详细的特征划分，局部划分初步就能达到要求。在分布式树中许多存在的近似算法都使用这个策略，也可以直接构造直方图近似（lightGBM直方图近似，速度更快，好像准确度有所降低），也可以使用其他的策略而不仅仅是分位法，分位策略便于分布式实现、计算方便。

 

3.3 加权分位法

近似计算中重要的一步是提出候选的分位点，特征百分比通常作为分布式划分的依据。考虑多重集合，key-value 为第样本的（样本点的第K维特征， 二阶导数），定义排序函数:

 

在以往的分位法中，没有考虑权值，许多存在的近似方法中，或者通过排序或者通过启发式方法（没有理论保证）划分。文章的贡献是提供了理论保证的分布式加权分位法。

3.4 稀疏自适应分割策略

在实际应用中，稀疏数据是不可避免的，造成稀疏数据的原因主要有：1 ，数据缺失。 2 ， 统计上的0 。 3 ， 特征表示中的one-hot形式，以往经验表明当出现稀疏、缺失值时时，算法需要很好的稀疏自适应。

 

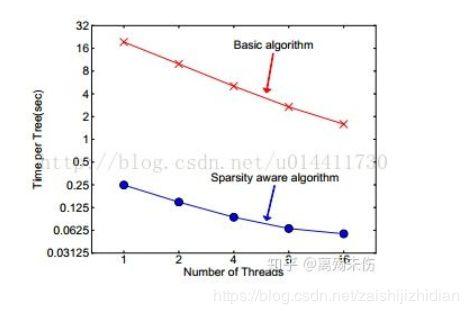
当出现特征值缺失时，实例被映射到默认的方向分支，关键是访问非缺失实体对Ik。现在的算法处理不存在的作为缺失值，学到处理缺失的最好方向，算法通过枚举一致性情况同样适用于用户指定的值。现有的树系统仅仅优化稠密的数据或者专注于处理有限的任务，例如：分类编码。XGBoost通过一种统一的方式处理所有的稀疏性情况。当出现稀疏情况的时候，稀疏性计算只有线性的计算复杂度。如图所示，稀疏自适应算法比基本的非稀疏数据算法快大约50倍。

 

正则化

正则化目标函数

对于一个含n个训练样本，m个features的结定数据集：D=(xi,yi)(|D|=n,xi∈Rm,yi∈R)D=(xi,yi)(|D|=n,xi∈Rm,yi∈R)，所使用的tree ensemble model使用K次求和函数来预测输出：

yi^=ϕ(xi)=∑k=1Kfk(xi),fk∈Fyi^=ϕ(xi)=∑k=1Kfk(xi),fk∈F

…… (1)

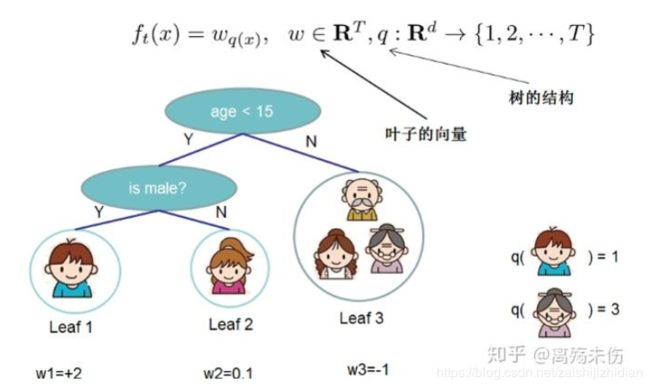
其中，F=f(x)=wq(x)，满足(q:Rm→T,w∈RT)F=f(x)=wq(x)，满足(q:Rm→T,w∈RT)，是回归树(CART)的空间。q表示每棵树的结构，它会将一个训练样本实例映射到相对应的叶子索引上。T是树中的叶子数。每个fkfk对应于一个独立的树结构q和叶子权重w。与决策树不同的是，每棵回归树包含了在每个叶子上的一个连续分值，我们使用wiwi来表示第i个叶子上的分值。对于一个给定样本实例，我们会使用树上的决策规则(由q给定)来将它分类到叶子上，并通过将相应叶子上的分值(由w给定)做求和，计算最终的预测值。为了在该模型中学到这些函数集合，我们会对下面的正则化目标函数做最小化：

L(ϕ)=∑il(yi^,yi)+∑iΩ(fk)L(ϕ)=∑il(yi^,yi)+∑iΩ(fk)

……(2)

其中：Ω(f)=γT+12λ||ω||2Ω(f)=γT+12λ||ω||2

其中，ll是一个可微凸loss函数（differentiable convex loss function），可以计算预测值yi^yi^与目标值yiyi间的微分。第二项ΩΩ会惩罚模型的复杂度。正则项可以对最终学到的权重进行平滑，避免overfitting。相类似的正则化技术也用在RGF模型(正则贪婪树)上。XGBoost的目标函数与相应的学习算法比RGF简单，更容易并行化。当正则参数设置为0时，目标函数就相当于传统的gradient tree boosting方法。

对缺失值处理

 

通常情况下，我们人为在处理缺失值的时候大多会选用中位数、均值或是二者的融合来对数值型特征进行填补，使用出现次数最多的类别来填补缺失的类别特征。

很多的机器学习算法都无法提供缺失值的自动处理，都需要人为地去处理，但是xgboost模型却能够处理缺失值，也就是说模型允许缺失值存在。

 

原是论文中关于缺失值的处理将其看与稀疏矩阵的处理看作一样。在寻找split point的时候，不会对该特征为missing的样本进行遍历统计，只对该列特征值为non-missing的样本上对应的特征值进行遍历，通过这个技巧来减少了为稀疏离散特征寻找split point的时间开销。在逻辑实现上，为了保证完备性，会分别处理将missing该特征值的样本分配到左叶子结点和右叶子结点的两种情形，计算增益后选择增益大的方向进行分裂即可。可以为缺失值或者指定的值指定分支的默认方向，这能大大提升算法的效率。如果在训练中没有缺失值而在预测中出现缺失，那么会自动将缺失值的划分方向放到右子树。

 

优缺点

xgboost的优势：

1、正则化

标准GBM的实现没有像XGBoost这样的正则化步骤。正则化对减少过拟合也是有帮助的。

实际上，XGBoost以“正则化提升(regularized boosting)”技术而闻名。

2、并行处理

XGBoost可以实现并行处理，相比GBM有了速度的飞跃，LightGBM也是微软最新推出的一个速度提升的算法。 XGBoost也支持Hadoop实现。

3、高度的灵活性

XGBoost 允许用户定义自定义优化目标和评价标准 。

4、缺失值处理

XGBoost内置处理缺失值的规则。用户需要提供一个和其它样本不同的值，然后把它作为一个参数传进去，以此来作为缺失值的取值。XGBoost在不同节点遇到缺失值时采用不同的处理方法，并且会学习未来遇到缺失值时的处理方法。

5、剪枝

当分裂时遇到一个负损失时，GBM会停止分裂。因此GBM实际上是一个贪心算法。XGBoost会一直分裂到指定的最大深度(max_depth)，然后回过头来剪枝。如果某个节点之后不再有正值，它会去除这个分裂。

这种做法的优点，当一个负损失（如-2）后面有个正损失（如+10）的时候，就显现出来了。GBM会在-2处停下来，因为它遇到了一个负值。但是XGBoost会继续分裂，然后发现这两个分裂综合起来会得到+8，因此会保留这两个分裂。

6、内置交叉验证

XGBoost允许在每一轮boosting迭代中使用交叉验证。因此，可以方便地获得最优boosting迭代次数。

而GBM使用网格搜索，只能检测有限个值。

7、在已有的模型基础上继续

XGBoost可以在上一轮的结果上继续训练。

sklearn中的GBM的实现也有这个功能，两种算法在这一点上是一致的。

缺点：发布时间短（2014），工业领域应用较少，待检验

应用场景

分类、回归

sklearn参数

xgboost 有很多可调参数，具有极大的自定义灵活性。比如说：

（1）objective [ default=reg:linear ] 定义学习任务及相应的学习目标，可选的目标函数如下：

“reg:linear” –线性回归。

“reg:logistic” –逻辑回归。

“binary:logistic” –二分类的逻辑回归问题，输出为概率。

“multi:softmax” –处理多分类问题，同时需要设置参数num_class（类别个数）

（2）’eval_metric’ The choices are listed below，评估指标:

“rmse”: root mean square error

“logloss”: negative log-likelihood

(3)max_depth [default=6] 数的最大深度。缺省值为6 ，取值范围为：[1,∞]

 

 

参考文章：

CART剪枝详解

机器学习算法梳理—XGBOOST--知乎专栏