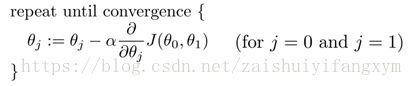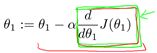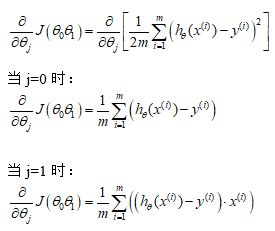吴恩达(Andrew Ng)《机器学习》课程笔记(1): 第1周——机器学习简介,单变量线性回归——梯度下降法
吴恩达(Andrew Ng)在 Coursera 上开设的机器学习入门课《Machine Learning》:
课程地址:https://www.coursera.org/learn/machine-learning
目录
一、引言
1.1、机器学习(Machine Learning)
2.1、监督学习(Supervised Learning)
(1) 什么是监督学习?
(2)监督学习分类:
3.1、无监督学习(Unsupervised Learning)
4.1、有监督学习和无监督学习的区别
二、单变量线性回归
2.1、模型表示
2.2、代价函数
2.3、代价函数直观理解
2.4、梯度下降法
2.5、梯度下降法直观理解
2.6、梯度下降的线性回归
三、线性代数回顾
3.1、矩阵和向量
3.2、加法和标量乘法
3.3、矩阵向量乘法
3.4、矩阵乘法
3.5、矩阵乘法性质
3.6、逆、转置
一、引言
1.1、机器学习(Machine Learning)
目前,机器学习没有准确的定义,用Tom Mitchell 提出机器学习定义:一个程序被认为能从经验E中学习,解决任务T,达到性能度量值P,当且仅当,有了经验E后,经过P判断,程序在处理T是时的性能有所提升。
通俗理解机器学习:机器从数据中学习,进而得到一个更加符合现实规律的模型,通过对模型的使用使得机器比以往表现的更好。
举个例子:
中学阶段,学生通过做大量的练习题,为的就是在高考解决问题。高考的题目一般来说是之前肯定没有遇到过的(无原题),但是这并不意味着这些题目我们无法解决。通过对之前所做过的练习题的分析,找到解题方法,同样可以解决陌生的题目,这就是人类的学习。机器学习就是模拟人类学习的过程。
机器学习其实就是将这一套方式运用到机器上,利用一些已知的数据(平时的练习题)来训练机器(做,让机器自己分析这些数据,并找到内在联系(学习解题方法),构建模型,从而对未知的数据(高考题)进行预测判定等。
2.1、监督学习(Supervised Learning)
(1) 什么是监督学习?
监督学习(Supervised Learning),用上述例子(做练习题和高考题)来解释,就是高考前所做的练习题是有标准答案(即标签)的。在学习的过程中,我们可以通过对照答案(标签),来分析问题找出方法,下一次在面对没有答案的问题时,往往也可以正确地解决。
对于机器学习来说,监督学习就是训练数据既有特征(feature)又有标签(label),通过训练,让机器可以自己找到特征和标签之间的联系,训练好后,在面对只有特征没有标签的数据时,可以判断出“标签”。
(2)监督学习分类:
回归(Regression ):
例如:通过做大量的练习题(分数即为标签),在高考时,预测你高考时的成绩。
分析:平时做题有分值,通过大量的练习题,在高考时,预测的值,也是一个连续的值。
分类(Classification):
例如:通过做大量的练习题(标签为1表示会做,标签为0表示不会做),在高考时,预测你高考时,某道题会不会做(即1或0)。
分析:因为预测的值,1表示会做,0表示不会做。因为只有少数的离散值,所以把他称为分类问题。
回归分析与分类区别其实就是数据的区别:回归是针对连续数据,分类是针对离散数据。
3.1、无监督学习(Unsupervised Learning)
例如:高中做练习题的例子,就是所做的练习题没有标准答案,换句话说,你也不知道自己做的是否正确,没有参照,想想就觉得是一件很难的事情。
但是就算不知道答案,我们还是可以大致的将语文,数学,英语这些题目分开,因为这些问题内在还是具有一定的联系。
这种问题在机器学习领域中就被称作聚类(Clustering),相对于监督学习,无监督学习显然难度要更大,在只有特征没有标签的训练数据集中,通过数据之间的内在联系和相似性将他们分成若干类。
谷歌新闻按照内容结构的不同分成军事、娱乐、体育等不同的标签,这就是一种聚类。
4.1、有监督学习和无监督学习的区别
简单的说:
有监督学习在训练的时候有标签;
无监督学习在训练的时候无标签。
二、单变量线性回归
2.1、模型表示
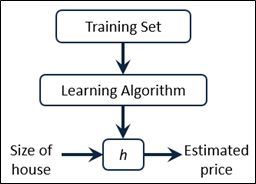
对于回归问题,一般流程为:
其中,h代表拟合的曲线,也称为学习算法的解决方案或函数或假设。 单变量的线性回归是回归问题的一种,它的表达式为:
![]()
由于它只有一个特征/输入变量x,同时它拟合的曲线是一条直线,所以该问题叫做单变量线性回归问题。
2.2、代价函数
以房屋价格为例,我们要选择合适的参数 ![]() 和
和 ![]() ,在房价问题上,这个问题就是选择直线中合适的斜率和截距。
,在房价问题上,这个问题就是选择直线中合适的斜率和截距。
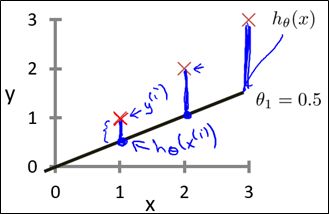
选择的参数直接决定了模型相对于训练集之间的准确程度。在模型预测得到的数据与真实值之间的距离(差距),就是建模误差(modeling error)。
我们的目的就是找到建模误差的平方和最小的参数![]() ,即代价函数最小
,即代价函数最小
代价函数(cost function):
目标:
![]() ,得到参数
,得到参数![]() 和
和 ![]() 。
。
2.3、代价函数直观理解
举一个简单的例子,
那么不同的![]() 就是过原点的直线,对于不同的参数
就是过原点的直线,对于不同的参数![]() ,得到不同斜率的直线,这些直线总有一条直线的似的代价函数值
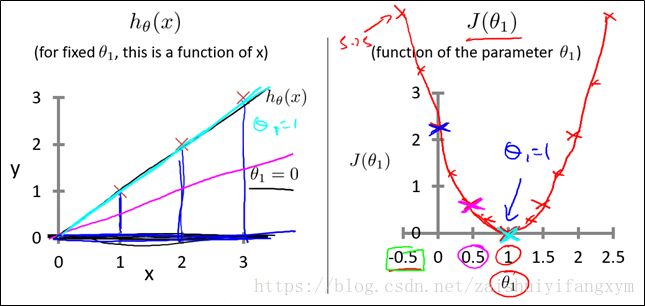
,得到不同斜率的直线,这些直线总有一条直线的似的代价函数值![]() 最小。那么不同参数得到不同的直线,不同直线得到代价函数的值,代价函数的曲线如下图所示,是一个二次函数,这下,要求出代价函数的最小值(即曲线最低点),即为最佳值。由图可知,当
最小。那么不同参数得到不同的直线,不同直线得到代价函数的值,代价函数的曲线如下图所示,是一个二次函数,这下,要求出代价函数的最小值(即曲线最低点),即为最佳值。由图可知,当![]() =1时,误差最小。
=1时,误差最小。
上面是一个简单的例子,参数只有一个,是![]() 和
和![]() 的变化曲线。那么参数
的变化曲线。那么参数 ![]() 和
和 ![]() 都变化,
都变化, ![]() ,
, ![]() 和
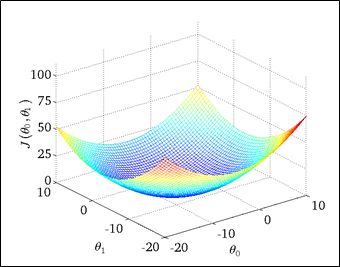
和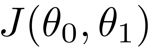 如下图所示:
如下图所示:
同样的方法,找到最低点,即为最佳值。但是,这需要编程将这西点绘制出来,然后人工找出最低点,这样比较复杂,只适合在低维数据的情况下,在高维数据情况下,上面的方法不可行,于是可以用梯度下降法来实现。
2.4、梯度下降法
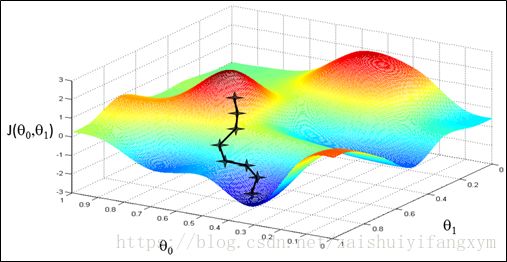
开始随机选择一个参数的组合![]() ,计算代价函数,然后我们寻找下一个能让代价函数下降最多的参数组合。我们持续这样做,直到到达一个局部最小值。由于我们没有尝试所有的参数组合,所以不能确定得到的结果是局部最小值还是全局最小值。
,计算代价函数,然后我们寻找下一个能让代价函数下降最多的参数组合。我们持续这样做,直到到达一个局部最小值。由于我们没有尝试所有的参数组合,所以不能确定得到的结果是局部最小值还是全局最小值。
梯度下降法的定义:
其中,α代表学习率(learning rate),它决定了沿着能让代价函数下降程度最大方向的步长。
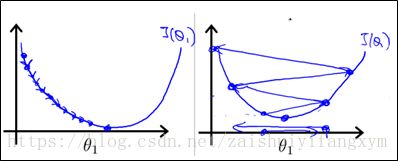
值得注意的是,![]() 是同时更新,也就是说:
是同时更新,也就是说:
如上图左图所示,为正确的更新过程,二者不同的地方在于,上图右图中在求![]() 的更新时,代价函数中的
的更新时,代价函数中的![]() 是已经更新过的了,而左图中的为将
是已经更新过的了,而左图中的为将![]() 都求过偏导之后再进行更新,代价函数中的
都求过偏导之后再进行更新,代价函数中的![]() 都是上一代中的值,与本次迭代更新无关。下面举例说明梯度下降的过程:
都是上一代中的值,与本次迭代更新无关。下面举例说明梯度下降的过程:
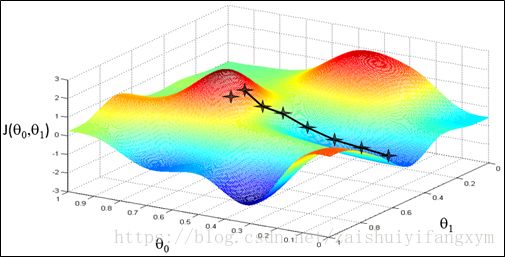
例如上图代表两座山,你现在所处的位置为最上面的那一点,你想以最快的速度达到山下,你环顾360度寻找能快速下山的方向,这个过程对应于求偏导的过程,你每次移动一步,移动的步长对应于α,当你走完这一步,然后接着环顾360度,寻求最快下山的方法,然后在走出一步,重复这个过程,直到走到山下,走到山下对应于找到了局部最小值
当然,参数不同,其有多种方法,找到不同的局部最小值。
2.5、梯度下降法直观理解
注意:下图中讨论,都是在![]() 的简单形式下讨论的。
的简单形式下讨论的。
(1)步长α(学习率)对梯度下降法的影响:
a. 当步长太小时,每次走的步子很小,导致到达最小值的速度会很慢,也就是收敛速度慢,但是能保证收敛到最小值点。
b. 当步长太大时,梯度下降法可能会越过最小值点,甚至可能无法收敛。
两种情况的示意图如下:
(2)梯度对梯度下降法的影响:
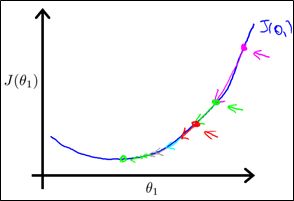
粉红色的点为初始点,在此点求出导数,然后乘以学习率,更新参数![]() ,到达第二个点,然后再在第二个点求导数,从斜率上明显可以看出,第二个点的斜率明显比第一个点的斜率低,也就是说虽然学习率固定,但是这一次更新的步长比上一次要小,以此类推,我们能够得出一个结论,当接近局部最低时,导数值会自动变得越来越小,所以梯度下降法会自动采用较小的幅度,这就是梯度下降的做法。所以实际上没有必要再另外减小α
,到达第二个点,然后再在第二个点求导数,从斜率上明显可以看出,第二个点的斜率明显比第一个点的斜率低,也就是说虽然学习率固定,但是这一次更新的步长比上一次要小,以此类推,我们能够得出一个结论,当接近局部最低时,导数值会自动变得越来越小,所以梯度下降法会自动采用较小的幅度,这就是梯度下降的做法。所以实际上没有必要再另外减小α
2.6、梯度下降的线性回归
梯度下降算法和线性回归算法如下图所示:
我们想用梯度下降算法来最小化代价函数,关键问题在于求导,即:
所以梯度下降算法修改为:
以上就是线性回归的梯度下降法。有时候也称为批量梯度下降法(batch gradient descent),因为在梯度下降的每一步中,我们都用到了所有的训练样本。
三、线性代数回顾
线性代数为基础知识,在我的博客有讲解关于: Matlab 基础知识——矩阵操作及运算, 有兴趣的可以参见我的博客:
https://blog.csdn.net/zaishuiyifangxym/article/details/81746332
3.1、矩阵和向量
3.2、加法和标量乘法
3.3、矩阵向量乘法
3.4、矩阵乘法
3.5、矩阵乘法性质
3.6、逆、转置
参考资料
[1] https://blog.csdn.net/bahuia/article/details/68926915
[2] https://blog.csdn.net/wyl1813240346/article/details/78366390
[3] https://blog.csdn.net/qq_34993631/article/details/79176274
[4] Andrew Ng Coursera 机器学习 第一周 PPT