webrtc video jitter buffer中的卡尔曼滤波器介绍(一)---概率论基础

首先弄明白基本点:

1.卡尔曼滤波器是用来干什么的?
2.如何使用卡尔曼滤波器？

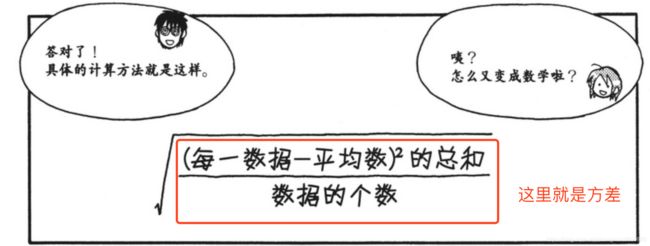
再此之前我们先补充一些高等数学统计学的基础只是:方差/均方误差/.

标准差的平方 = 方差
标准差表示的数据的离散程度.

举个例子吧，以下例子取自:漫画统计学，日本人出版的，写的非常的通俗易懂，强烈推荐大学去看看.

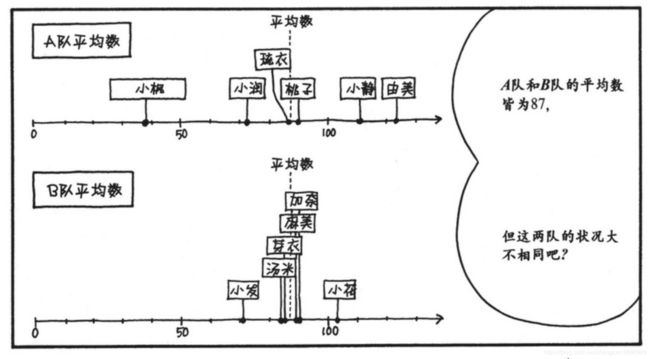
有三个球队，他们的成绩如图所示:

这个时候，这三个球队的平均数如下图所示.

仅仅通过平均数是无法代表更直观的理解数据的。

C队存在229这样的超级数，很明显不能代表整体的实力.

A队和B队的平均数更是一样的，更加不好分析,把他们的数据转化为更容易理解的数据图.

很明显的我们能看到B队的成绩中，靠近平均数的成员更多，也就是数据的离散程度小。

因此为了更好的分析数据，我们引入了标准差的概念,引入标准差的概念来表示数据的离散程度。

从公式可以看出，离散程度越小，方差也就越小，标准差也就越小。
反之，离散程度越大，方差也就越大，标准差也就越大

B队的离散程度更小，因此方差也就小，标准差也就小.

上面的基本概念整理明白了，我们来深入进一步去了解正态分布，正态分布是讲概率的，首先我们弄明白正态分布的由来.

下面是一组学生的成绩;

单纯的数字看起来，太不直观了，接下来我们我们转为图标，并且通过图表直观的显示，学习成绩范围内比列:

通过图表我们可以看到:
[50 - 60 ]这个区间的成绩大概占40%左右.

接着我们不断的调小区间:

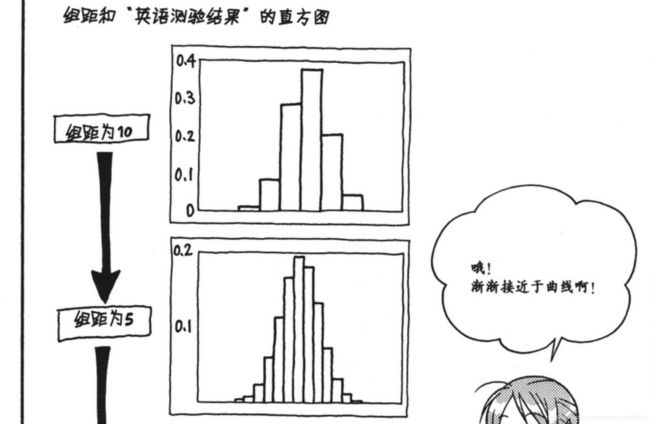
继续把区间不断的调整:

当区间不断的调小的时候，我们会发现，我们得到了一条曲线.
这个曲线就是我们正态分布曲线.

更神奇的是，我们可以用一个公式，结合前面说的平均值，标准差，直接表示出这条正态曲线.

接下来就是见证神奇的地方了.

而标准差和平均值则决定了这个正态分布曲线的形状.

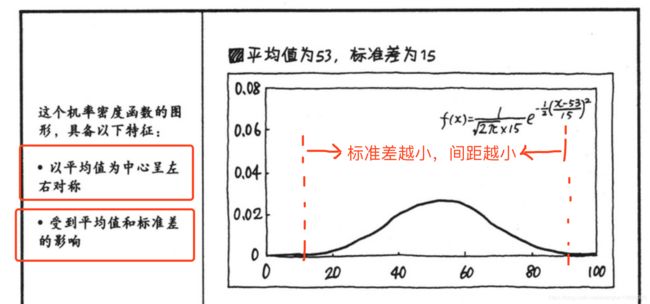
正态分布的曲线 ：
1.以平均值为中心，左右对称
2.标准差越小，曲线越陡,也就是曲线的高峰越陡峭.

比如上一张是平均值为53，标准差为15的图.
接下来我们看看平均值为53，标准差为5的图.

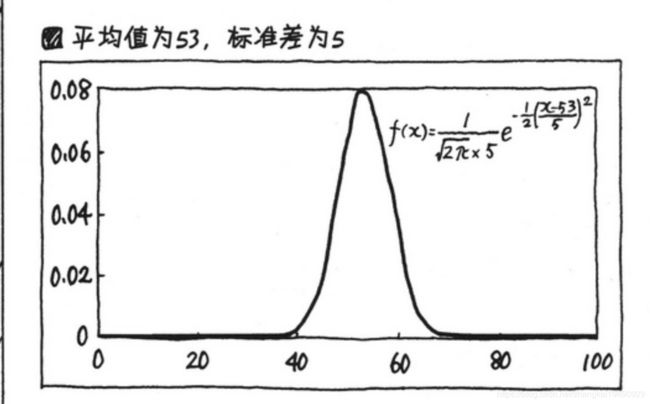
对比下这2张图,第二张图陡峭多了.

接下来我们来介绍协方差的概念:
https://www.zhihu.com/question/20852004/answer/134902061

上面这篇文章已经写的相当不错了，大家可以参考下.

协方差是一种表示相关性的分析手段。
协方差>0表示正相关.
协方差<0表示负相关.

我们举个例子:

2条单调递增的直线,现在我们求这2条单独递增的直线的协方差.

第一条线A: 1 / 3/ 5 / 7/ 9 — 平均数为:5
第二条线B: 2 / 4 / 6 /8 / 10 — 平均数为: 6

OK,协方差公式为:

根据公式，我们来求A和B的公式:

Cov(A,B) =[ (1 - 5)(2 - 6) + ( 3 - 5)(4-6) + (5-5)(6-6) + (7-5)(8-6) + (9-5)*(10-6) ] / 5

我们可以求出:

Cov(A,B) = 8 ,也就是正相关的属性，他们的趋势是一致的.

协方差越大，表示2者的趋势越接近，反之，越小则表明两者的趋势相反.

引用参考文献:

1.如何通俗的理解卡尔曼滤波
https://www.zhihu.com/question/23971601/answer/137325095

2.我所理解的卡尔曼滤波
https://www.jianshu.com/p/d3b1c3d307e0