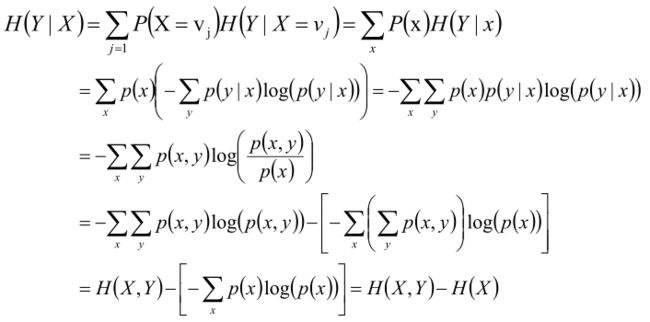机器学习(决策树一)——最直白的话来说信息熵
接下来几篇博客介绍决策树,并且尽量用最直白的话来讲解。本篇博客介绍决策树中比较重要的一个概念——信息熵。
前置内容
信息熵可以说是决策树中最基本的概念,在介绍信息熵前,补充一点儿前置内容。
假设存在一组随机变量X,各个值出现的概率关系如图
![]()
现在有一组由X变量组成的序列: BACADDCBAC…;如果现在希望将这个序列转换为二进制来进行网络传输,那么我们得到一个这样的序列:01001000111110010010…
也就是: 在这种情况下,我们可以使用两个比特位来表示一个随机变量。
即,我们的期望值为: E = 2 E=2 E=2
而当X变量出现的概率值不一样的时候,对于一组序列信息来讲,每个变量平均需要多少个比特位来描述呢??
![]()
此时可以:
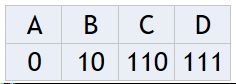
这个编码怎么来的呢?可以使用哈夫曼编码啊……
从而得到期望值:
E = 1 ∗ 1 2 + 2 ∗ 1 4 + 3 ∗ 1 8 + 3 ∗ 1 8 E=1*\frac{1}{2}+2*\frac{1}{4}+3*\frac{1}{8}+3*\frac{1}{8} E=1∗21+2∗41+3∗81+3∗81
换一种表达
E = − log 2 ( 1 2 ) ∗ 1 2 − log 2 ( 1 4 ) ∗ 1 4 − log 2 ( 1 8 ) ∗ 1 8 − log 2 ( 1 8 ) ∗ 1 8 E=-\log _2 \left( \frac{1}{2}\right) * \frac{1}{2}-\log _2 \left( \frac{1}{4}\right) * \frac{1}{4}-\log _2 \left( \frac{1}{8}\right) * \frac{1}{8}-\log _2 \left( \frac{1}{8}\right) * \frac{1}{8} E=−log2(21)∗21−log2(41)∗41−log2(81)∗81−log2(81)∗81
一般化
假设现在随机变量 X X X 具有 m m m 个值,分别为: V 1 , V 2 , . . . . , V m V_1 ,V_2 ,....,V_m V1,V2,....,Vm ;并且各个值出现的概率如下表所示;那么对于一组序列信息来讲,每个变量平均需要多少个比特位来描述呢??
![]()
可以使用这些变量的期望来表示每个变量需要多少个比特位来描述信息:
E ( X ) = − p 1 log 2 ( p 1 ) − p 2 log 2 ( p 2 ) − . . . − p m log 2 ( p m ) = − ∑ i = 1 m p i log 2 ( p i ) E(X)=-p_1 \log _2 (p_1) - p_2 \log _2 (p_2)- ... -p_m \log _2 (p_m) = -\sum _{i=1}^m p_i \log_2(p_i) E(X)=−p1log2(p1)−p2log2(p2)−...−pmlog2(pm)=−i=1∑mpilog2(pi)
这里的 E ( X ) E(X) E(X) 就叫做随机变量 X X X 的信息熵。
信息熵(Entropy)
H ( X ) = − ∑ i = 1 m p i log 2 ( p i ) H(X)=-\sum _{i=1}^m p_i \log_2(p_i) H(X)=−i=1∑mpilog2(pi)
补充:数学与物理中信息熵的含义不一样。
信息量:指的是一个样本/事件所蕴含的信息,如果一个事件的概率越大,那么就可以认为该事件所蕴含的信息越少。极端情况下,比如:“太阳从东方升起”,这不是废话吗?他那么一说,你那么一听,可能转身就忘记了,因为是确定事件,所以不携带任何信息量;明天股市大涨,很不确定的事件,信息量会大很多。
信息熵:1948年,香农引入信息熵;一个系统越是有序,信息熵就越低,一个系统越是混乱,信息熵就越高,所以信息熵被认为是一个系统有序程度的度量。
这里提到了“有序”,这和我们传统理解的可不一样。
有序:比如前置内容的例子,如果变量都是一个取值,比较有序,而不是ABCABCABC叫有序。也就是绝大多数都是A或绝大多数都是B……这叫有序。
简单的说一下,系统中只有两种事件:A和B。按上面的思路,系统越有序,信息熵越低,则在系统中体现在,要不全是A要不全是B;系统越混乱,信息熵越高,则在系统中是一半A一半B。
反过来,可以理解(不考虑什么有序无序,因为这里单纯就是机器学习),如果信息熵低,表示这个样本空间,某样本出现的概率比较大的,这个事件出现地次数是最多的:如果信息熵比较高的话,表示所有事件出现的概率是比较均等的,没有非常大概率的事件,也没有非常小概率的事件。
所以说:信息熵就是用来描述系统信息量的不确定度。
这里总结一下:系统越混乱,即越无序,也就是越没有比较大概率的样本出现,则表示不确定性性越高,即信息熵越大;反之,信息熵越小。
图形化
High Entropy(高信息熵):表示随机变量X是均匀分布的,各种取值情况是等概率出现的。
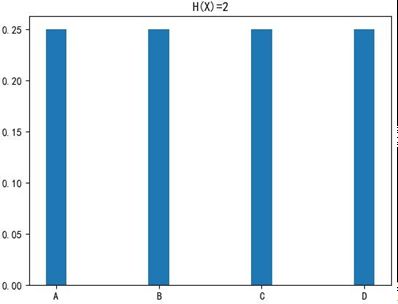
Low Entropy(低信息熵):表示随机变量X各种取值不是等概率出现。可能出现有的事件概率很大,有的事件概率很小。
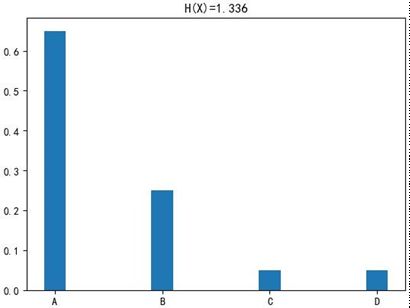
举例
赌马比赛中,有两组赛马,每组有ABCD四个编号的,共八匹,获胜的概率如下:
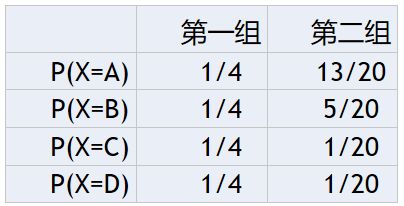
在比赛前,对于第一组而言,我们只知道A/B/C/D获胜的概率是一样的,我们是判断不出来任何偏向的(如果让你买的话,可能抛硬币猜一下,或选择抓阄);但是对于第二组而言,我们很清楚的就能够判断A是最可能获胜。
条件熵
跟条件概率很类似的,其实相当于把样本量缩小了,也可以理解为把样本空间进行了划分。
定义
给定条件X的情况下,随机变量Y的信息熵就叫做条件熵。
举例
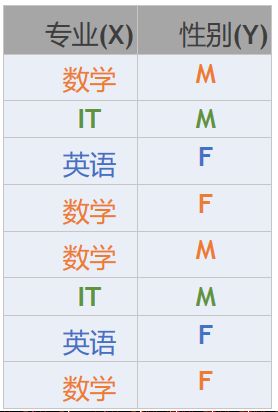
可以得到:

当专业(X)为数学的时候,求:Y的信息熵的值H(Y|X=数学)

H ( Y ∣ X = 数 学 ) = − 1 2 ∗ log 2 ( 1 2 ) − 1 2 ∗ log 2 ( 1 2 ) = 1 H (Y | X = 数学)= -\frac{1}{2} * \log_2 \left( \frac{1}{2} \right)-\frac{1}{2} * \log_2 \left( \frac{1}{2} \right)=1 H(Y∣X=数学)=−21∗log2(21)−21∗log2(21)=1
那么:给定条件X的情况下,所有不同x值情况下Y的信息熵的平均值叫做条件熵。
H ( Y ∣ X ) = ∑ j = 1 P ( X = v j ) H ( Y ∣ X = v j ) H(Y|X)=\sum_{j=1}P(X=v_j)H(Y|X=v_j) H(Y∣X)=j=1∑P(X=vj)H(Y∣X=vj)
所以:
H ( Y ∣ X ) = 0.5 ∗ 1 + 0.25 ∗ 0 + 0.25 ∗ 0 = 0.5 H(Y|X)=0.5*1+0.25*0+0.25*0=0.5 H(Y∣X)=0.5∗1+0.25∗0+0.25∗0=0.5
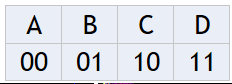
还有另外一个公式
H ( Y ∣ X ) = H ( X , Y ) − H ( X ) H(Y|X)=H(X,Y)-H(X) H(Y∣X)=H(X,Y)−H(X)
事件(X,Y)发生所包含的熵,减去事件X单独发生的熵,即为在事件X发生的前提下,Y发生“新”带来的熵,这个也就是条件熵本身的概念。但是利用累加的那种方式居多.
总:
现在理解下来,信息熵的概念是不是不那抽象了。