《现代操作系统》精读与思考笔记 第二章 进程和线程
转载:http://www.cnblogs.com/wuyuegb2312/p/3406569.html
本系列博文是《现代操作系统(英文第三版)》(Modern Operating Systems,简称MOS)的阅读笔记,定位是正文精要部分的摘录和课后习题精解,因此不会事无巨细的全面摘抄,仅仅根据个人情况进行记录和推荐。由于是英文版,部分内容会使用英文原文。
课后习题的选择标准:尽量避免单纯的概念考察(如:What is spooling?)或者简单的数值计算,而是能够引起思考加深理解的题目。为了保证解答的正确性,每道题都会附上原书解答,而中文部分会适当加入自己的见解。原书答案下载地址(需注册)
从本节开始,新增“概念名称回顾”,不会展开来写,仅供按图索骥、查漏补缺,方便回顾。上一节也会补上。
概念名称回顾
进程:相关API、状态、实现;
线程:和进程的区别与联系、内核级线程和用户级线程区别和实现及优劣;
进程通信:竞争条件、临界区、互斥与忙等、信号量、互斥锁、管程、消息传递、屏障
调度算法:不同系统的不同调度算法、机制与策略分离;
典型IPC问题:哲学家进餐问题、读者—写者问题
1.关于进程数目、进程平均I/O频率与CPU利用率的推导
原书P94假设进程用于等待I/O结束的时间为它运行的总时间中的p(比如,p=80%代表这个进程I/O花费的时间是总运行时间的80%),同一时间内内存中一共有n个进程在运行,那么这n个进程都在等待I/O的概率为pn——这意味着所有的进程都没用使用CPU,也即CPU处在空闲状态——那么,根据对立事件的概率,CPU利用率就可以表示为:
CPU 利用率 = 1 - p^n
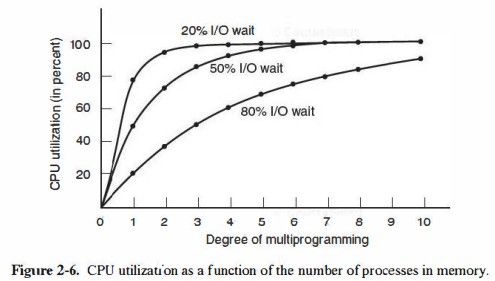
利用这个公式做图表,会得到很多有价值的结论。
可以看出,(1)在进程数相同时,I/O频率越高,CPU的利用率越低;(2)为了提高CPU的利用率,可以采取的方法是增加同时运行的进程数。
虽然这个公式是把I/O频率平均化所得的近似公式,并且假定这n个进程之间的运行互不干扰;更准确的模型需要用排队论的知识进行构建,但是,“增加进程数以使得CPU更不常处于空闲状态”的结论,依然正确,并与上图仅仅有着轻微的不同。
这个简单模型甚至还能得到另一个推断:如果计算机拥有512MB内存,操作系统占用了128MB,其余进程I/O频率都是80%,并且每个占用128MB,那么此时的CPU利用率是1-0.83,也即49%;而当增加512MB内存时,意味着可以运行更多的4个进程,这时CPU的利用率会提升到79%,也即这额外的512MB内存带来了30%的CPU利用率提升。
更神奇的是,这个简单模型还可以用来计算多个进程并行时所需使用的总时间,例子请参考习题5。
2.Peterson解法
原书P123,为了能够保证进程互斥地进入临界区(critical_region),并要求只使用软件编码实现(不提供额外的硬件机制),最初可以想到的解决方法如下,它被称为严格轮换法(Strict Alternation):
//process 0
while(TURE) {
while(turn != 0)
;/*loop*/
critical_region();
turn = 1;
noncritical_region();
}
//process 1
while(TURE) {
while(turn != 1)
;/*loop*/
critical_region();
turn = 0;
noncritical_region();
} 虽然可以保证互斥这一要求,但是这两个进程只能轮流进入临界区,这意味着较快的一个进程会被较慢的另一个所拖慢。也即,当process0刚退出临界区而使得turn=1、process1在非临界区时,process0不能马上再次进入临界区,这违反了(原文中的前文“一个好的临界区访问方式”的)条件3,这4个条件如下:
1.任何两个进程不能同时进入同一个临界区;
2.不应做出有关CPU速度或个数的任何假设;
3.任何不在它的临界区的进程不应阻塞其他进程;
4.不应有任何进程无限地等待进入临界区。
看来这个根据直觉写出的解法并不令人满意。为了从软件角度解决这个问题,不同人提出了不同的算法。Peterson于1981年发现了一个相当简单的解法:
#define FALSE 0
#define TRUE 1
#define N 2 /* number of processes */
int turn; /* whose turn is it? */
int interested[N]; /* all values initially 0 (FALSE) */
void enter_region(int process) /* process is 0 or 1 */
{
int other; /* number of the other process*/
other = 1 - process; /* the opposite of process */
interested[process] = TRUE; /* show that you are interested */
turn = process; /* set flag */
while(turn == process && interested[other] == TRUE)
; /* null statement */
}
void leave_region(int process) /* process: who is leaving */
{
interested[[process] = FALSE; /* indicate departure from critical region */
} 稍作分析可以看出,如果只有一个进程,可以无限运行下去;如果有两个进程,它们都标记了自己对临界区感兴趣(interested[process] = TRUE),但此时turn由后设置者决定。而先设置者p0正好可以退出while循环,执行临界区代码,并于退出临界区时声明自己对临界区无兴趣(interested[[process] = FALSE)。这时,如果另一个进程p1在忙等,则可以进入临界区;如果不在忙等,它的interseted要么非真(未执行到这个语句),要么为真但尚未开始进行忙等:对于前者,如果p0足够快,可以再次进入临界区;对于后者,p0就只能开始忙等,等待p1先进入临界区了。
读者可能对上面我的转述看的一头雾水,没关系,自行根据代码和情形假设推导下各个情况才能理解这个解法的妙处。我个人认为这段代码妙处在于,它用了两个变量(一个整型和一个2个元素的数组)而非单一变量来提供更好的解法,这个思路非常值得学习。
3.实时系统中周期任务可调度的条件的推导
原书P161,假设一个实时系统中所有任务都是周期性的,一共有m个任务,第i个任务周期为Pi,需要时间Ci的CPU才能处理完,那么这些任务可调度的条件是
[\sum_{i=1}^{m}\frac{C_{i}}{P_{i}}\leq 1]
原书没有解释这个式子怎么推导的,我这里做一个简单的解释:首先,对所有分式进行通分,其分母就表示了一个“大周期”,在这个“大周期”里,任务i被执行的次数就是它在分子中的系数。只要分子小于等于分母,也即分数值小于等于1,这些任务便可以在这个“大周期”中执行所需执行的次数,并且不会逾期。同时,对于某个任务,其C/P大于1,那么无论如何这些任务都是不可调度的。
4.哲学家进餐问题
这部分完整描述在原书P164~167。当初学习汤子瀛版《计算机操作系统》时,这个问题的解决一种是加了限制条件的普通信号量(《现代操作系统》图2-45的解法与之类似),另一种是同时对两个数据操作的AND型信号量。下面看看图2-46给出的既能保证不死锁,又能最大化同时进餐的哲学家数目的解法:
#define N 5 /* number of philosophers */
#define LEFT (i+N-1)%N /* number of i's left neighbor */
#define RIGHT (i+ 1)%N /* number of i's right neighbor */
#define THINKING 0 /* philosopher is thinking */
#define HUNGRY 1 /* philosopher is trying to get forks */
#define EATING 2 /* philosopher is eating */
typedef int semaphore; /* semaphores are a special kind of int */
int state[N]; /* array to keep track of everyone's state */
semaphore mutex = 1 ; /* mutual exclusion for critical regions */
semaphore s[N]; /* one semaphore per philosopher */
void philosopher(int i) /* i: philosopher number, from 0 to N-1 */
{
while (TRUE) { /* repeat forever */
think(); /* philosopher is thinking */
take_ forks(i); /* acquire two forks or block */
eat(); /* yum-yum, spaghetti */
put_ forks(i); /* put both forks back on table */
}
}
void take_forks(int i) /* i: philosopher number, from 0 to N-1 */
{
down(&mutex); /* enter critical region */
state[i] = HUNGRY; /* record fact that philosopher i is hungry */
test(i); /* try to acquire 2 forks */
up(&mutex); /* exit critical region */
down(&s[i]); /* block if forks were not acquired */
}
void put_forks(i) /* i: philosopher number, from 0 to N-1 */
{
down(&mutex); /* enter critical region */
state[i] =THINKING; /* philosopher has finished eating */
test(LEFT); /* see if left neighbor can now eat */
test( RIGHT); /* see if right neighbor can now eat */
up(&mutex); /* exit critical region */
}
void test(i) /* i: philosopher number, from 0 to N-1 */
{
if (state[i] ==HUNGRY && state[LEFT] != EATING && state[RIGHT] != EATING) {
state[i] = EATING;
up(&s[i]);
}
} 这种对自身状态的标记,与上面提到的Perterson解法思路很类似。这里的临界区,是所有哲学家的状态state[]数组,只有合法的状态转换才允许继续,如果两边的哲学家至少有一边在吃,就会被阻塞,而这个阻塞会在两边发生状态转化时被测试是否可以被唤醒,非常巧妙的解法。课后45、46题是对这个解法的进一步讨论,直接列在下面,由于不难理解,没有翻译。
45. In the solution to the dining philosophers problem (Fig. 2-46), why is the state variable set to HUNGRY in the procedure take_forks?
Answer:
The change would mean that after a philosopher stopped eating, neither of his neighbors could be chosen next. In fact, they would never be chosen. Suppose that philosopher 2 finished eating. He would runtest for philosophers 1 and 3, and neither would be started, even though both were hungry and both forks were available. Similarly, if philosopher 4 finished eating, philosopher 3 would not be started. Nothing would start him.
- Consider the procedure put_forks in Fig. 2-46. Suppose that the variable state[i] was set to THINKING after the two calls to test, rather than before. How would this change affect the solution?
Answer:
If a philosopher blocks, neighbors can later see that she is hungry by checking his state, in test , so he can be awakened when the forks are available.
课后习题选
4.When an interrupt or a system call transfers control to the operating system, a kernel stack area separate from the stack of the interrupted process is generally used. Why?
译:
当中断或系统调用使得系统的控制权交给操作系统时,所用的内核栈通常与用户栈是分开的,为什么这么设计?
Answer:
There are several reasons for using a separate stack for the kernel. Two of them are as follows. First, you do not want the operating system to crash because a poorly written user program does not allow for enough stack space. Second, if the kernel leaves stack data in a user program’s memory space
upon return from a system call, a malicious user might be able to use this data to find out information about other processes.
答案译文:
这有原因,其中两个是:第一,用户栈可能很小,如果内核栈不是独立的而是使用用户栈的一部分,那么系统会因空间不足崩溃;第二,当返回用户空间时,恶意用户可以通过自己的栈(由中断或系统调用时产生的)残留的内容获取别的进程的信息。
5.Multiple jobs can run in parallel and finish faster than if they had run sequentially. Suppose that two jobs, each of which needs 10 minutes of CPU time, start simultaneously. How long will the last one take to complete if they run sequentially? How long if they run in parallel? Assume 50% I/0 wait.
译:两个I/O频率都为50%、都需要10分钟CPU时间的任务,顺序运行需要多少时间?并行运行需要多少时间?
Answer:
If each job has 50% I/O wait, then it will take 20 minutes to complete in the absence of competition. If run sequentially, the second one will finish 40 minutes after the first one starts. Withtwo jobs, the approximate CPU utilization is 1 − 0.52. Thus each one gets 0.375 CPU minute per minute of real time. To accumulate 10 minutes of CPU time, a job must run for 10/0.375 minutes, or about 26.67 minutes. Thus running sequentially the jobs finish after 40 minutes, but running in parallel they finish after 26.67 minutes.
分析:
顺序执行的时候,根据I/O频率为50%、CPU时间10分钟,那么分别需要20分钟,一共就是40分钟。
并行时,根据正文文第2条介绍,CPU利用率为1 − 0.52,这意味着每分钟每个进程并行时实际获得用于处理的CPU时间是0.75/2 = 0.375分钟,那么执行完需要10分钟的CPU时间的工作实际使用了10/0.375 = 26.67分钟。又由于是并行的,相当于二者同时完成,因此是26.67分钟。
我一开始简单地认为并行时只需要20分钟,但是明显是没有依据的,即使是并行,单个单核心单线程CPU(这是本章的假设之一)在某个时刻而非某一个时期内仍然只能执行一个任务。
26.Show how counting semaphores (i.e., semaphores that can hold an arbitrary value) can be implemented using only binary semaphores and ordinary machine instructions.
译:
如何用二值信号量和一些机器指令实现计数信号量。
Answer:
Associated with each counting semaphore are two binary semaphores, M ,used for mutual exclusion, and B , used for blocking. Also associated with each counting semaphore is a counter that holds the number of ups minus the number of downs, and a list of processes blocked on that semaphore. To implement down, a process first gains exclusive access to the semaphores, counter, and list by doing a down on M . It then decrements the counter. If it is zero or more, it just does an uponM and exits. If M is negative, the process is put on the list of blocked processes. Then an upis done on M and a down is done on B to block the process. To implement up, first M is downed to get mutual exclusion, and then the counter is incremented. Ifit is more than zero, no one was blocked, so all that needs to be done is to up M. If, however, the counter is now negative or zero, some process must be removed from the list. Finally, an upis done on B and M in that order.
答案译文:
用两个二值信号量和一个计数器counter实现一个计数信号量:M用于互斥,B用于阻塞,counter用于记录up减去down的次数,再用一个链表来记录阻塞在这个计数信号量上的进程。
down的实现:进程先对M进行down来获得counter、链表的独占访问权,并把counter减1。如果counter大于等于0,直接对M进行up即可;否则,记录在链表再up,然后对B进行down从而阻塞这个进程。
up的实现:进程同样先对M进行down,count加1,若其大于0,直接对M进行up即可;否则count小于等于0,把链表中一个进程移出,然后对B、M依次up。
勘误:
1.P163的2.5标题下方,”… we will examine three of the …”,而本节实际上一共只介绍了两种
2.P166的图2-46,put_forks(i)的函数定义缺少i的类型int
3.P173.习题46应为Fig.2-46而非2-20