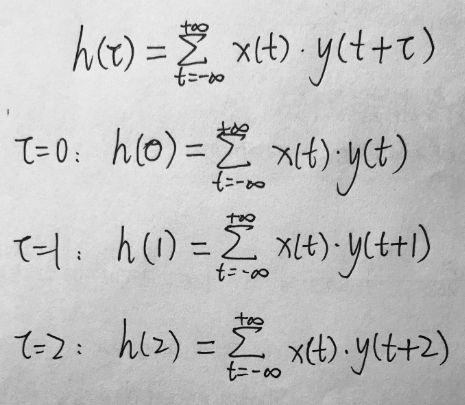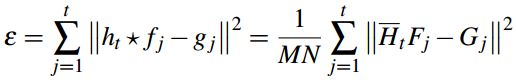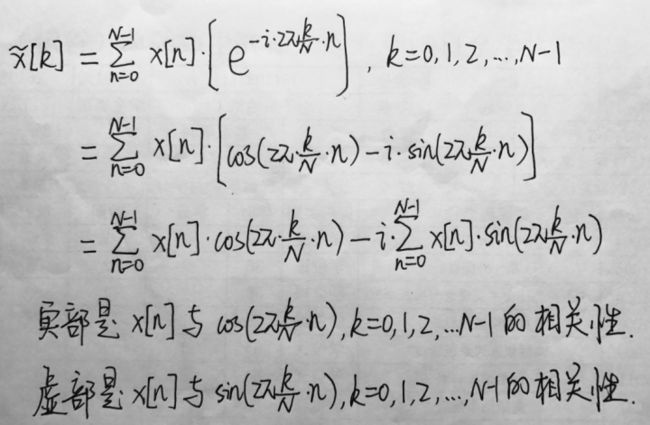目标跟踪图谱
【原文:https://zhuanlan.zhihu.com/p/27914504】
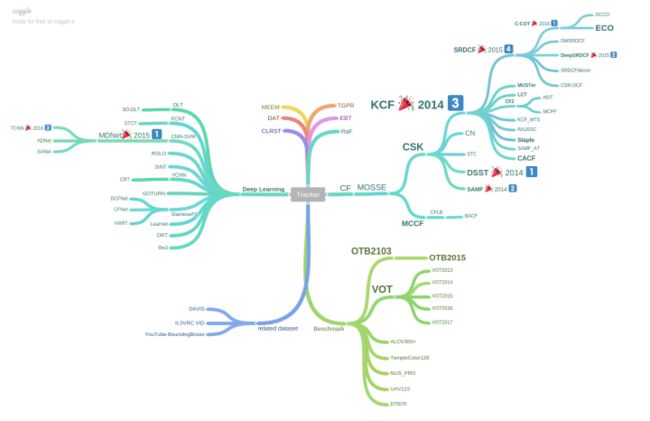
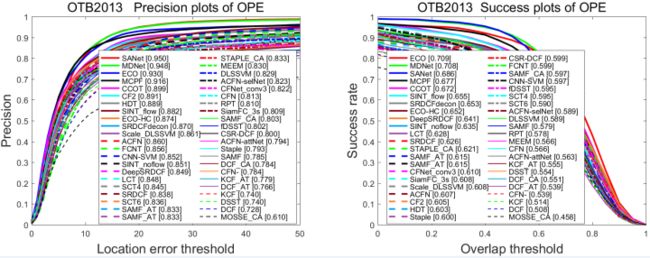
先上图,benchmark更新了,借用一下图片,版权归王强所有,来自这里 foolwood/benchmark_results:
目标跟踪阶段性总结
截止CVPR 2017,tracking的目前发展如上图,Tracking方向还是以相关滤波CF和深度学习DL两大阵营为主:
- 右半边是相关滤波CORR. FILTER,根据特征分两小类:结合hand-craft特征如HOG(Histogram of Oriented Gradient), CN(Color Names)或Color Histogram的相关滤波,速度可以做到很快,同时精度也很好,ECO-HC和Staple;结合CONV. FEAT.卷积特征的相关滤波可以做到最好精度,而且预训练CNN模型的卷积特征非常强力,而且泛化能力非常优秀,但速度差一些,如ECO目前位于tracking领域的顶端。总结:相关滤波性能的提升离不开深度学习。
- 左边是深度学习Deap Learning,采用CNN+end2end traning,也可以分两小类:以精度为主从CNN-SVM到MDNet,及扩展TCNN, ADNet, SANet,在测试集上可以比肩顶尖相关滤波算法,但由于训练集的限制,泛化能力可能尚有疑问(具体情况请等待VOT 2017的结果,去年的冠军TCNN没中任何会议~~);速度为主的SiamFC,及扩展DCFNet, CFNet和HART,在GPU上能达到远超实时的速度,尤其DCFNet和CFNet引入CF layer,相关滤波在CNN框架中实现end2end训练,让卷积特征提取可以配合相关滤波检测,实现联动,让CNN框架也可以实现密集检测,精度和速度都能达到较高水平。总结:深度学习框架中可以加入相关滤波层端到端训练。
综上,CF和DL已经不是对立关系了,互相融合互相促进是发展方向,或许已不存在两大阵营。
目前tracking领域亟待解决的难题,仅供参考:
- 以HOG特征为代表的相关滤波可以做到很快的速度,但HOG特征的旋转不变性很差,也就是说这类算法对平面类旋转基本无解。MD大神最新论文DCCO证明深层卷积特征具有较好的旋转不变性,但引入卷积特征会损失速度优势。如何保证速度的同时解决平面旋转问题?
- 不管是卷积特征和端到端训练的CNN框架,速度都是硬伤,forward passing time是设计网络的关键,搭建小网络代替常用的VGG-16以期实现CPU上实时,CNN模型的压缩加速是目前研究的热点之一;但CNN需要海量训练数据,目前缺乏这样的数据库,做到训练集和测试集严格独立,才能保证算法的泛化能力。如果引入深度学习后解决CPU上无法实时的问题?
ICCV 2017的相关论文过段时间再来分析,等VOT2017的结果出来吧,到时候论文代码也应该就开源了,也留给我时间慢慢读论文。。
最近专栏更新比较慢,一半是VOT结果还是没出,另一半是我在学习其他方向,要与时俱进还是很不容易的。如果有必要,我也会和大家分享一些其他方向的干货论文,感谢支持。
***********************************分割线********************************
速度优化trick
很多人问我速度怎么优化,真的没有什么秘密。这里介绍一个在C-COT和ECO中大量使用的加速方法,保守估计该trick的加速比在20%以上,而且是完全没有任何性能损失的trick,但在这两篇论文中完全没有提到,下面这段话来自C-COT的Supplementary Material:
Since the Fourier coefficients of a real function obey the Hermitian symmetry, we only need to process half the Fourier coefficients 0 ≤ k ≤ K. This effectively halves the computations and memory consumption of the training procedure.
相关滤波速度的来源之一就是滤波操作在傅里叶域进行,这一加速trick简单来说就是利用实数傅里叶谱的共轭对称性减少一半的计算量和内存消耗。
从基础开始介绍。首先来分析图像的傅里叶系数:
clear
close all
fys = imread('fys.bmp');
img = rgb2gray(fys);
figure(1),
subplot(1,2,1),imshow(fys,[]);
subplot(1,2,2),imshow(img,[]);
fc = fft2(double(img));
figure(2),
subplot(1,3,1),imshow(log(real(fc)),[]);
subplot(1,3,2),imshow(log(imag(fc)),[]);
subplot(1,3,3),imshow(log(real(fc).^2 + imag(fc).^2),[]);
fcc = fftshift(fc);
figure(3),
subplot(1,3,1),imshow(log(real(fcc)),[]);
subplot(1,3,2),imshow(log(imag(fcc)),[]);
subplot(1,3,3),imshow(log(real(fcc).^2 + imag(fcc).^2),[]);结果如下,首先是读入图像并灰度化:
然后计算傅里叶谱并显示,依次是实部,虚部和幅值,这时候傅里叶谱的中心在左上角点,这时候可能很难看出对称性:
fftshift移频操作,将中心移动到图像中心,这时候对称性就非常清晰了,注意是共轭对称性:
所以C-COT和ECO在计算图像特征的fft时会多了fftshift移频操作,傅里叶正变换被封装成这样:
function xf = cfft2(x)
% Find the data type
data_type_complex = complex(zeros(1, 'like', x));
% calculate output size
in_sz = size(x);
% if both dimensions are odd
if all(mod(in_sz(1:2), 2) == 1)
xf = fftshift(fftshift(fft2(x), 1), 2);
else
out_sz = in_sz;
out_sz(1:2) = out_sz(1:2) + mod(out_sz(1:2)+1,2);
% allocate
xf = zeros(out_sz, 'like', data_type_complex);
xf(1:in_sz(1),1:in_sz(2),:,:) = fftshift(fftshift(fft2(x), 1), 2);
if out_sz(1) ~= in_sz(1)
xf(end,:,:,:) = conj(xf(1,end:-1:1,:,:));
end
if out_sz(2) ~= in_sz(2)
xf(:,end,:,:) = conj(xf(end:-1:1,1,:,:));
end
end傅里叶逆变化被封装成这样:
function x = cifft2(xf)
if isa(xf, 'gpuArray')
x = real(ifft2(ifftshift(ifftshift(xf, 1), 2)));
else
x = ifft2(ifftshift(ifftshift(xf, 1), 2), 'symmetric');
end有了对称性,接下来在所有频谱计算都只需要计算频谱的一半,这部分直接降低计算量50%,特征的频谱系数在经过一些列预处理以后,直接压缩为紧凑傅里叶系数如下代码:
function xf = compact_fourier_coeff(xf)
% Creates a compact fourier series representation by removing the strict right
% half plane.
if iscell(xf)
xf = cellfun(@(xf) xf(:,1:(size(xf,2)+1)/2,:), xf, 'uniformoutput', false);
else
xf = xf(:,1:(size(xf,2)+1)/2,:);
end最后,计算好滤波器的频谱系数之后,根据共轭对称性补全频谱系数就可以了,频谱重构如下代码:
function xf = full_fourier_coeff(xf)
% Reconstructs the full Fourier series coefficients.
if iscell(xf)
xf = cellfun(@(xf) cat(2, xf, conj(rot90(xf(:,1:end-1,:), 2))), xf, 'uniformoutput', false);
else
xf = cat(2, xf, conj(rot90(xf(:,1:end-1,:), 2)));
end就是这么简单,这么NIUBILITY,没有任何代价的相关滤波加速技巧,并没有出现的论文中,或许他认为太简单了,MD大神只在C-COT的Supplementary Material 中section 3 的最后提了一下。
只要是相关滤波算法,这一trick就是普适的,没有理由不用,LET'S MOVE!
**********************************分割线********************************
相关滤波的直观解释
近期一直在思考,如何以简单易懂的方式向他人解释相关滤波是什么,为什么能够在tracking任务中work?以下是我参考各位大神的网上资源,给出的一种比较形象但并不严谨的思路,写下来供大家参考,或许对理解相关滤波有点帮助。
乘积和:最简单的相似度度量。将两个离散信号对应位置相乘,结果越大,说明两个信号越相似。单一数值的信号为例:
- 两个正数相乘或两个负数相乘,结果都是正数;一正一负相乘,结果是负数。符号一致的信号相似度肯定比符号相反的信号更相似,对应乘积越大,满足以上结论。
- (5*5=25) > (4*6=24) > (3*7=21)。平均值相等的一组信号,两个数值越接近的信号肯定越相似,对应乘积越大,也满足以上结论。
这就是最简单的信号相似度度量方法。如果是两个一维或者二维离散信号,对应位置的数值相乘,再将所有乘积求和,乘积和就可用于表示这两个信号的相似度。
常用的线性相关系数就有类似定义:
注意多了去均值和归一化。
信号相关。为了方便理解,这里只分析离散信号,连续信号积分相当于离散信号求和,就不重复说明了。离散信号x(t)和离散信号y(t)的互相关h的定义如下:
通过详细分解各项可以看出,离散信号h中每一项的值h(a),都是信号x和平移a单位后的信号y之间,对应位置离散值的乘积和。上面介绍过这乘积和表示两个信号之间的相似度,所以得到直观解释:信号相关就是两个信号经各种不同平移之后的相似度。
为什么要这样定义呢?举个例子,要描述sin和cos这两个离散信号之间的相似度,如果不平移,我们直接计算对应位置离散值的乘积和,只能得到的一个非常小的值,说明相似度很低;但事实上这两个信号非常相似,根据上面互相关定义,计算不同平移后的乘积和,就能得到一组相似度值,反映不同时延下的相似度,这样才能更加客观公正的描述两个信号的相似性。
信号相关要求计算很多很多次乘积和,速度肯定是难以接受的,万幸我们有傅里叶变换,空域相关等价于频域点乘,原本复杂的空域计算流程,转换为将两个信号分别傅里叶变换到频域,然后点乘,结果逆变换回空域,就得到了互相关信号。
推广到在tracking。将相关的定义推广到二维,相关滤波类算法在滤波器训练和更新阶段,通过最优化方法构建这样一个相关滤波器h,其响应越大能表示与检测目标越相似:
之后,检测阶段只需要计算相关滤波器和待检测图像块之间的相关性,相关性的定义会帮助我们计算每个循环移位图像块和相关滤波器之间的相似度,最大响应点代表最相似位置,也就是目标所在的新位置。
傅里叶变换的相关性解释。傅里叶变换其实就是计算目标信号与不同频率正弦、余弦信号的相关性,即傅里叶级数就是目标信号与不同频率sin、cos信号之间的相似度。下面详细解释:傅里叶变换的定义如下图:
根据wiki上离散傅里叶变换DFT的定义,稍作变形:
傅里叶系数的实部是信号x与不同频率cos信号的对应位置离散值的乘积和,即x与不同频率余弦信号的相似度;
傅里叶系数的虚部是信号x与不同频率sin信号的对应位置离散值的乘积和,即x与不同频率正弦信号的相似度;
经过傅里叶变换,目标信号被分解为与一组基信号中每个信号的相似度,基信号包含不同频率的正弦波和余弦波。DFT过程与向量在正交坐标系上的分解可以类比。
空域信号相关等价于频域点乘,即对应频率基信号的傅里叶系数相乘,相乘就是计算相似度,结果表示两个信号在该频率的相似度。
参考资料:
【图片】【简单向】用最简单易懂的方式实现FFT【c语言吧】_百度贴吧
傅里叶分析之掐死教程(完整版)更新于2014.06.06