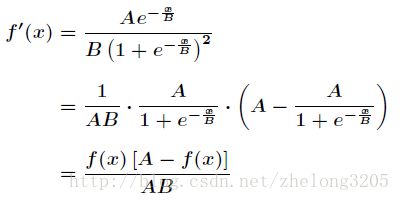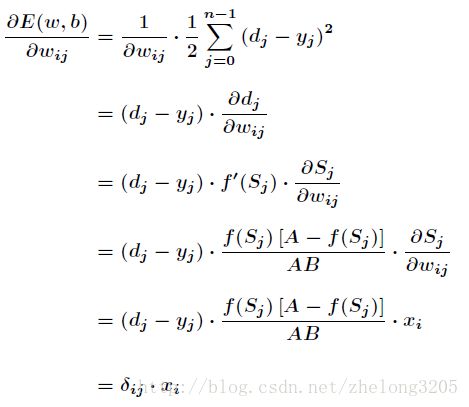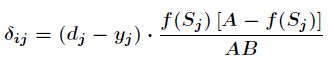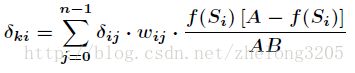机器学习之BP神经网络 以及 tensorflow 实现

BP （Back Propagation）神经网络简介 ：

先介绍一下神经元，在生物神经网络中，每个神经元与其它神经元相连，当一个神经元“兴奋”时，就会通过穿出神经向其它神经元发送化学物质，其它神经元会通过穿人神经接受信息然后再传递至神经中枢处理信息。现在机器学习中的神经网络就是基于生物学中的神经元模型的。一个一个的神经元与其它神经元相互连接构成所谓的神经网络。

BP 神经网络分为两个过程
1. 工作信号正向传递子过程
2. 误差信号逆向传递过程

在一般的BP神经网络中，单个样本有m个输入和n个输出，在输入层和输出层之间还有若干个隐藏层，实际上 1989年时就已经有人证明了一个万能逼近定理 ：
在任何闭区间的连续函数都可以用一个隐藏层的BP神经网络进行任意精度的逼近。
所以说一个三层的神经网络就可以实现一个任意从m维到n维的一个映射。这三层分别是
输入层、隐藏层、输出层 如图所示 ：

关于隐藏层的选择 ：
在BP神经网路中，输入层和输出层的节点数目都是固定的，关键的就是在于隐藏层数目的选择，隐藏层数目的选择决定了神经网络工作的效果

一般而言，有一个关于隐藏层数目的经验公式

其中 h 为隐藏层节点数目，m为输入层节点数目，n为输出层节点数目 a 为 1-10 之间的调节常数。一般而言如果数据多的话我们可以设a稍微大一点，而数据不是太多的时候就设置的小一点防止过拟合。

正向传递子过程 ：
设节点 i 与 节点 j 之间的权值 为 wij，节点 j 的阀值为 bj，每个节点的输出值为 xj，具体的计算方法如下

其中 f 为激活函数 ，一般选择sigmoid函数或者 线性函数正向传播中输入层没有阀值

BP神经网络的关键之处就在于反向误差的传播
假设我的第j个输出结果为 dj 则误差函数如下所示 ：

BP神经网络的墓地就是通过不断修改 w 值 和 b 值使得误差达到最小 （因为一旦 w b 值全部确定以后，一个输入就对应着一个输出，所以只要让误差最小就可以了）而调整误差的方法就是使用梯度下降法不断减小误差。

我们选择激励函数为

对于介于隐藏层与输出层之间的权值wij 由偏微分公式我们可以得到

对于激励函数求导 （为了方便我们得到整体的导数）我们可以得到

然后对于wij 的偏导数我们也可以求出

其中 ：

对于bj的导数为

这就是著名的学习规则，通过改变神经元之间的连接权值来减少系统实际输出和期望输出的误差，这个规 则又叫做Widrow-Hoff学习规则或者纠错学习规则。

对最后一层处理完毕之后我们开始对前一层进行处理，首先将误差通过权值向前传递得到上一层的误差，那么同样的对于上一层使用梯度下降法最小化误差就可以了／

剩下的就是根据梯度下降法更新w与b的值，以使得误差最小

都是一样的方法调整误差就可以了

标准BP神经网络的缺陷：
（1）容易形成局部极小值而得不到全局最优值。
BP神经网络中极小值比较多，所以很容易陷入局部极小值，这就要求对初始权值和阀值有要求，要使得初始权值和阀值随机性足够好，可以多次随机来实现。
（2）训练次数多使得学习效率低，收敛速度慢。
（3）隐含层的选取缺乏理论的指导。
（4）训练时学习新样本有遗忘旧样本的趋势。
通常BP神经网络在训练之前会对数据归一化处理，即将数据
映射到更小的区间内，比如[0,1]或[-1,1]。

tensorflow 在 moist 上的实现代码

import tensorflow as tf 
from  tensorflow.examples.tutorials.mnist  import  input_data
import numpy as np 

mnist = input_data.read_data_sets('data', one_hot = True)

num_classes = 10
input_size = 784
hidden_units_size = 30
batch_size = 100
training_iterations = 10000

X = tf.placeholder (tf.float32, shape = [None, input_size])
Y = tf.placeholder (tf.float32, shape = [None, num_classes])

W1 = tf.Variable (tf.random_normal ([input_size, hidden_units_size], stddev = 0.1))
B1 = tf.Variable (tf.constant (0.1), [hidden_units_size])
W2 = tf.Variable (tf.random_normal ([hidden_units_size, num_classes], stddev = 0.1))
B2 = tf.Variable (tf.constant (0.1), [num_classes])

hidden_opt = tf.matmul (X, W1) + B1
hidden_opt = tf.nn.relu (hidden_opt)
final_opt = tf.matmul (hidden_opt, W2) + B2
final_opt = tf.nn.relu (final_opt)

loss = tf.reduce_mean (tf.nn.softmax_cross_entropy_with_logits (labels = Y, logits = final_opt))
opt = tf.train.GradientDescentOptimizer (0.05).minimize (loss)
init = tf.global_variables_initializer ()
correct_prediction = tf.equal (tf.argmax (Y, 1), tf.argmax (final_opt, 1))
accuracy = tf.reduce_mean (tf.cast (correct_prediction, 'float'))

sess = tf.Session ()
sess.run (init)
for i in range (training_iterations) :
    batch = mnist.train.next_batch (batch_size)
    batch_input = batch[0]
    batch_labels = batch[1]
    training_loss = sess.run ([opt, loss], feed_dict = {X: batch_input, Y: batch_labels})
    if i % 1000 == 0 :
        train_accuracy = accuracy.eval (session = sess, feed_dict = {X: batch_input,Y: batch_labels})
        print ("step : %d, training accuracy = %g " % (i, train_accuracy))