一、实验目的及基本要求
设计和实现最佳置换算法、先进先出置换算法、最近最久未使用置换算法、页面缓冲置换算法,改进Clock算法;
通过页面访问序列随机发生器实现对上述算法的测试及性能比较。
二、页面置换算法相关知识
如果发生了缺页中断,就需要从磁盘上将需要的页面调入内存。如果内存没有多余的空间,就需要在现有的页面中选择一个页面进行替换。使用不同的页面置换算法,页面更换的顺序也会各不相同。如果挑选的页面是之后很快又要被访问的页面,那么系统将很开再次产生缺页中断,因为磁盘访问速度远远内存访问速度,缺页中断的代价是非常大的。因此,挑选哪个页面进行置换不是随随便便的事情,而是有要求的。
1.页面置换的目标
页面置换时挑选页面的目标主要在于降低随后发生缺页中断的次数或概率。
因此,挑选的页面应当是随后相当长时间内不会被访问的页面,最好是再也不会被访问的页面。但是,如果可能,最好选择一个没有修改过的页面,这样替换时就无须将被替换页面的内容写回磁盘,从而进一步加快缺页中断的响应速度。
所以,为了达到这个目的,设计出了各种各样的页面置换算法,下面就来看看这些算法。
三、页面置换算法
1.最佳置换算法
从主存中移出永远不再需要的页面;如无这样的页面存在,则选择最长时间不需要访问的页面。于所选择的被淘汰页面将是以后永不使用的,或者是在最长时间内不再被访问的页面,这样可以保证获得最低的缺页率。
2.先进先出置换算法
是最简单的页面置换算法。这种算法的基本思想是:当需要淘汰一个页面时,总是选择驻留主存时间最长的页面进行淘汰,即先进入主存的页面先淘汰。其理由是:最早调入主存的页面不再被使用的可能性最大。
3.最近最久未使用置换算法
这种算法的基本思想是:利用局部性原理,根据一个作业在执行过程中过去的页面访问历史来推测未来的行为。它认为过去一段时间里不曾被访问过的页面,在最近的将来可能也不会再被访问。所以,这种算法的实质是:当需要淘汰一个页面时,总是选择在最近一段时间内最久不用的页面予以淘汰。
4.页面缓冲置换算法
设立空闲页面链表和已修改页面链表采用可变分配和基于先进先出的局部置换策略,并规定被淘汰页先不做物理移动,而是依据是否修改分别挂到空闲页面链表或已修改页面链表的末尾,空闲页面链表同时用于物理块分配,当已修改页面链表达到一定长度如Z个页面时,一起将所有已修改页面写回磁盘,故可显著减少磁盘I/O操作次数。
5.改进Clock算法
改进型Clock置换算法的主要思想是,在每次页面替换时,总是尽可能地先替换掉既未被访问又未被修改的页面。
在将一个页面换出时,如果该页已被修改过,便须将该页重新写回到磁盘上;但如果该页未被修改过,则不必将它拷回磁盘。在改进型Clock算法中,除须考虑页面的使用情况外,还须在增加一个因素,即置换代价,这样页面换出时,既要是未使用过的页面,又要是未被修改过的页面。把同时满足这两个条件的页面作为首选淘汰的页面。由访问位A和修改位M可以组合成下面四种类型的页面:
- 1类(A=0,M=0):表示该页最近既未被访问,又未被修改,是最佳淘汰页。
- 2类(A=0,M=0):表示该页最近未被访问,但已被修改,并不是很好的淘汰页。
- 3类(A=1,M=0):表示该页最近已被访问,但未被修改,该页有可能在被访问。
- 类(A=1,M=1):表示该页最近已被访问且被修改,该页可能再被访问。
三、课题要求细化说明
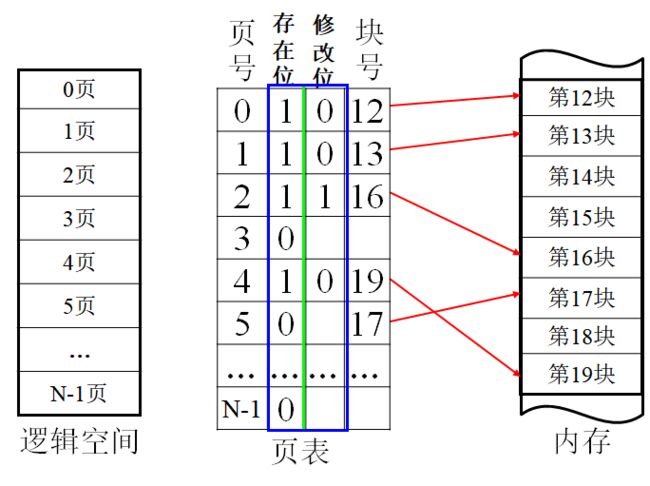
- 页表用整数数组或结构数组来表示。
- 页面访问序列串是一个整数序列,整数的取值范围为0到N - 1。页面访问序列串中的每个元素p表示对页面p的一次访问。
- 符合局部访问特性的随机生成算法。
- 确定虚拟内存的尺寸N,工作集的起始位置p,工作集中包含的页数e,工作集移动率m(每处理m个页面访问则将起始位置p +1),以及一个范围在0和1之间的值t;
- 生成m个取值范围在p和p + e间的随机数,并记录到页面访问序列串中;
- 生成一个随机数r,0 ≤ r ≤ 1;
- 如果r < t,则为p生成一个新值,否则p = (p + 1) mod N;
- 如果想继续加大页面访问序列串的长度,请返回第2步,否则结束。
四、相关数据结构设计
根据各个算法的特点,程序实现的过程中用到的数据结构主要有以下两种
- 数组:定义的时候利用指针定义,然后根据全局变量block设定的给进程分配的物理内存的块数动态分配内存。一旦完成内存分配,不再改变数组的大小。
用到数组结构来实现的算法程序有:最佳置换算法,先进先出置换算法,最近最久未使用置换算法,改进型置换算法。 - 队列:为单向队列,队列长度仍然由全局变量指定。
用到队列的算法程序有:先进先出置换算法。队列结点元素的结构体如下:
typedef struct node
{
int num;//页号
node* next;//下一个结点页面
} Node, *pNode;
typedef struct queue
{
int n;//总的结点数
pNode front;//队首指针
pNode rear; //队尾指针
} Queue, *pQueue;
- 链表:主要是将装入内存的页块串联起来。
用到链表的算法程序:页面缓冲算法。链表结点元素的结构体如下:
struct LNode
{
int data;//页号
int flag;//访问位
int modify;//修改位
LNode* next;
};
struct Link
{
int num;//当前链表上的结点数
LNode* next;
};
五、主要函数功能说明
1.最佳置换算法
int block = 3;
int access[32]; //访问序列
int* memo;
int lost = 0;//没找到的页面数
int index = 0;//指示当前下标
在程序最开始定义了一些全局变量,包括物理块的个数、访问序列数组、内存指针、缺页数目等。
void generate()
{
int maxLength, e, m, p;
double t;
printf("请输入要随机生成访问序列的长度\n");
scanf("%d", &maxLength);
printf("请输入页面数\n");
scanf("%d", &e);
printf("请输入工作集起始位置\n");
scanf("%d", &p);
printf("请输入工作集移动效率\n");
scanf("%d", &m);
printf("请输入0-1之间的t\n");
scanf("%lf", &t);
srand((unsigned)time(NULL));
int iterNum = 0;
int index=0;
for (int i = 0; i < maxLength;)
{
if (i + m >= maxLength)
iterNum = maxLength - i;
else
iterNum = m;
for (int j =0;j在这个void generate()函数中,按照第三节的内容进行了函数的构造。
符合局部访问特性的随机生成算法。
- 确定虚拟内存的尺寸N,工作集的起始位置p,工作集中包含的页数e,工作集移动率m(每处理m个页面访问则将起始位置p +1),以及一个范围在0和1之间的值t;
- 生成m个取值范围在p和p + e间的随机数,并记录到页面访问序列串中;
- 生成一个随机数r,0 ≤ r ≤ 1;
- 如果r < t,则为p生成一个新值,否则p = (p + 1) mod N;
- 如果想继续加大页面访问序列串的长度,请返回第2步,否则结束。
void initMemo()
{
memo = (int*) malloc (block * sizeof (int));
int i = 0;
for (; i < block; i++)
{
memo[i] = -1;
}
return;
}
在void initMemo()这个函数中,对内存指针进行了内存分配与初始化。
int isInMemo (int n)
{
int i = 0;
for (; i < block; i++)
{
if (access[n] == memo[i])
{
return 1;
}
}
return 0;
}
在int isInMemo (int n)中,查询指定页号是否已经在内存中。
void optimal (int n)
{
int i = 0, j = 0;
if (isInMemo (n))
{
printf ("----------------------以下页面已被调入,无置换----------------------\n");
}
else
if (index == block)
{
lost++;
int max = 0, pos, tag;
for (i = 0; i < block; i++)
{
tag = -1;
for (j = n + 1; j < 32; j++)
{
if (access[j] == memo[i])
{
tag = j;
break;
}
}
if (tag == -1)
{
max = 32;
pos = i;
break;
}
else
{
if (max < tag)
{
max = tag;
pos = i;
}
}
}
memo[pos] = access[n];
}
else
{
memo[index] = access[n];
index++;
}
}
void optimal (int n)是访问一个页面,执行一次最佳置换算法的主函数,
void testOptimal()
{
initMemo();
int i = 0;
printf ("最佳置换算法:\n");
for (; i < 32; i++)
{
optimal (i);
printf ("%d %d %d\n", memo[0], memo[1], memo[2]);
}
printf ("最佳置换算法缺页率: %2f \n缺页数为: %d\n", lost / 32.0, lost);
lost = 0;
free (memo);
index = 0;
}
void testOptimal()对算法进行了封装与实现,是测试使用的主函数。
int main()
{
initMemo();
generate();
testOptimal();
printf("\n");
system("pause");
return 0;
}
定义了程序入口。
2.先进先出置换算法
int access[32];//访问序列
int size = 3;//给进程分配的内存的大小
int lost = 0;//缺页数
在程序最开始定义了一些全局变量,包括物理块的个数、访问序列数组、缺页数目等。
void generate()
{
int maxLength, e, m, p;
double t;
printf("请输入要随机生成访问序列的长度\n");
scanf("%d", &maxLength);
printf("请输入页面数\n");
scanf("%d", &e);
printf("请输入工作集起始位置\n");
scanf("%d", &p);
printf("请输入工作集移动效率\n");
scanf("%d", &m);
printf("请输入0-1之间的t\n");
scanf("%lf", &t);
srand((unsigned)time(NULL));
int iterNum = 0;
int index=0;
for (int i = 0; i < maxLength;)
{
if (i + m >= maxLength)
iterNum = maxLength - i;
else
iterNum = m;
for (int j =0;jvoid generate()同上小节。
typedef struct node
{
int num;
struct node* next;
} Node, *pNode;
typedef struct queue
{
int n;
pNode front;
pNode rear;
} Queue, *pQueue;
定义了两种数据结构体。
void initQueue (pQueue q)
{
q->rear = (pNode) malloc (sizeof (Node));
if (q->rear == NULL)
{
printf ("failed\n");
}
else
{
q->front = q->rear;
q->rear->next = NULL;
q->front->next = NULL;
q->n = 0;
}
}
void initQueue (pQueue q)初始化队列。
void push (pQueue q, int num)
{
pNode p = (pNode) malloc (sizeof (Node));
if (p == NULL)
{
printf ("failed");
}
else
{
p->next = NULL;
p->num = num;
if (q->front == q->rear)
{
q->front->next = p;
q->rear = p;
}
else
{
q->rear->next = p;
q->rear = p;
}
q->n++;
}
}
void push (pQueue q, int num)是在队列中加入新的页面结点。
void pop (pQueue q)
{
pNode p;
if (q->front != q->rear)
{
p = q->front->next;
q->front->next = p->next;
if (p == q->rear)
{
q->front = q->rear;
}
q->n--;
free (p);
}
}
void pop (pQueue q)将页面移出内存。
void destroy (pQueue q)
{
while (q->front != q->rear)
{
pop (q);
}
}
void destroy (pQueue q)销毁队列释放内存。
int findInQueue (pQueue q, int num)
{
pNode p;
if (q->front != q->rear)
{
p = q->front->next;
while (p)
{
if (p->num == num)
{
return 1;
}
else
{
p = p->next;
}
}
}
return 0;
}
int findInQueue (pQueue q, int num)查找页面是否已经调入内存。
void fifo (pQueue q, int num)
{
if (findInQueue (q, num))
{
printf ("----------------------以下页面已被调入,无置换----------------------\n");
}
else
{
if (q->n == size)
{
pop (q);
push (q, num);
lost++;
}
else
{
push (q, num);
}
}
}
void fifo (pQueue q, int num)每访问一个页面,执行一次算法。
void fifoTest()
{
Queue q;
pNode p;
initQueue (&q);
int i = 0;
printf ("先进先出置换算法\n");
for (; i < 32; i++)
{
fifo (&q, access[i]);
p = q.front->next;
while (p)
{
printf ("%d ", p->num);
p = p->next;
}
printf ("\n");
}
printf ("先进先出算法缺页率:%2f \n缺页数为: %d\n", lost / 32.0, lost);
destroy (&q);
}
void fifoTest()先进先出置换算法实现函数。
int main()
{
generate();
fifoTest();
return 0;
}
程序入口。
3.最近最久未使用置换算法
int block = 3;
int access[32]; //访问序列
int* memo;
int lost = 0;//没找到的页面数
int index = 0;//指示当前下标
设置全局变量。
void generate()
{
int maxLength, e, m, p;
double t;
printf("请输入要随机生成访问序列的长度\n");
scanf("%d", &maxLength);
printf("请输入页面数\n");
scanf("%d", &e);
printf("请输入工作集起始位置\n");
scanf("%d", &p);
printf("请输入工作集移动效率\n");
scanf("%d", &m);
printf("请输入0-1之间的t\n");
scanf("%lf", &t);
srand((unsigned)time(NULL));
int iterNum = 0;
int index=0;
for (int i = 0; i < maxLength;)
{
if (i + m >= maxLength)
iterNum = maxLength - i;
else
iterNum = m;
for (int j =0;j同上。
void initMemo()
{
memo = (int*) malloc (block * sizeof (int));
int i = 0;
for (; i < block; i++)
{
memo[i] = -1;
}
return;
}
初始化内存。
int isInMemo (int n)
{
int i = 0;
for (; i < block; i++)
{
if (access[n] == memo[i])
{
return 1;
}
}
return 0;
}
判断是否在内存中。
void LRU (int n)
{
int i, j;
if (isInMemo (n))
{
printf ("----------------------以下页面已被调入,无置换----------------------\n");
}
else
if (index == block)
{
int max = n, pos = -1, tag;
for (i = 0; i < block; i++)
{
for (j = n - 1; j >= 0; j--)
{
if (access[j] == memo[i])
{
tag = j;
break;
}
}
if (tag < max)
{
max = tag;
pos = i;
if (max == 0)
{
break;
}
}
}
memo[pos] = access[n];
lost++;
}
else
{
memo[index] = access[n];
index++;
}
}
LRU算法主函数,每执行一次查询置换一页。
void testLRU()
{
int i;
initMemo();
printf ("最近最久未使用算法\n");
for (i = 0; i < 32; i++)
{
LRU (i);
printf ("%d %d %d\n", memo[0], memo[1], memo[2]);
}
printf ("最近最久未使用缺页率: %2f \n缺页数为: %d\n", lost / 32.0, lost);
lost = 0;
index = 0;
free (memo);
}
封装函数。
int main()
{
initMemo();
generate();
testLRU();
printf("\n");
system("pause");
return 0;
}
程序入口。
4.改进型Clock置换算法
typedef struct Lnode
{
int data;
int flag;//访问位
int modify;//修改位
} LNode;
设置对应结构体。
int block = 3;
int access[32]; //访问序列
int lost = 0,index=0;//没找到的页面数
LNode* nodes;//改进型Clock置换算法用到的数据结构
初始化全局变量。
void generate()
{
int maxLength, e, m, p;
double t;
printf("请输入要随机生成访问序列的长度\n");
scanf("%d", &maxLength);
printf("请输入页面数\n");
scanf("%d", &e);
printf("请输入工作集起始位置\n");
scanf("%d", &p);
printf("请输入工作集移动效率\n");
scanf("%d", &m);
printf("请输入0-1之间的t\n");
scanf("%lf", &t);
srand((unsigned)time(NULL));
int iterNum = 0;
int index=0;
for (int i = 0; i < maxLength;)
{
if (i + m >= maxLength)
iterNum = maxLength - i;
else
iterNum = m;
for (int j =0;j同上。
int isInNodes (int n)
{
int i;
for (i = 0; i < block; i++)
{
if (nodes[i].data == access[n])
{
return 1;
}
}
return 0;
}
页面是否已经在链表中
void updated_Clock (int n)
{
if (isInNodes (n))
{
printf ("----------------------以下页面已被调入,无置换----------------------\n");
}
else
if (index == block)
{
lost++;
int i = 0, tag = -1;
while (1)
{
if ( (i / block) % 2 == 0)
{
if (nodes[i % block].flag == 0 && nodes[i % block].modify == 0)
{
tag = i % block;
break;
}
}
if ( (i / block) % 2 == 1)
{
if (nodes[i % block].flag == 0 && nodes[i % block].modify == 1)
{
tag = i % block;
break;
}
else
{
nodes[i % block].flag = 0;
}
}
i++;
}
nodes[tag].data = access[n];
nodes[tag].flag = 1;
if (rand() % 10 < 4)
{
nodes[tag].modify = 1;
}
else
{
nodes[tag].modify = 0;
}
}
else
{
nodes[index].data = access[n];
nodes[index].flag = 1;
if (rand() % 10 < 4)
{
nodes[index].modify = 1;
}
else
{
nodes[index].modify = 0;
}
index++;
}
}
每访问一个新的页面,执行一次算法。
void test_Clock()
{
int i = 0, j = 0;
printf ("改进型Clock置换算法\n");
nodes = (LNode*) malloc (block * sizeof (LNode));
for (i = 0; i < block; i++)
{
nodes[i].data = -1;
nodes[i].flag = -1;
nodes[i].modify = -1;
}
for (i = 0; i < 32; i++)
{
updated_Clock (i);
for (j = 0; j < block; j++)
{
printf ("%d ", nodes[j].data);
}
printf ("\n");
}
printf ("改进型Clock置换算法缺页率: %2f \n缺页数为: %d\n", lost / 32.0, lost);
lost = 0;
index = 0;
}
改进型clock算法实现函数。
int main()
{
generate();
test_Clock();
}
程序入口。
5.页面缓冲算法
typedef struct Lnode
{
int data;
int flag;//访问位
int modify;//修改位
struct LNode* next;
}LNode;
typedef struct Link
{
int num;//当前链表上的结点数
LNode* next;
}Link;
建立链表结构体。
int size = 3;
int p;//工作集的起始位置
int table[32];//物理内存,每一个元素代表一个页面
int access[32]; //访问序列
int memo[3] = { -1, -1, -1 };
int lost = 0;//没找到的页面数
int index = 0;//指示当前下标
LNode* nodes;//PBA用到的数据结构
Link idle;
Link modified;
初始化全局变量。
void generate()
{
int maxLength, e, m, p;
double t;
printf("请输入要随机生成访问序列的长度\n");
scanf("%d", &maxLength);
printf("请输入页面数\n");
scanf("%d", &e);
printf("请输入工作集起始位置\n");
scanf("%d", &p);
printf("请输入工作集移动效率\n");
scanf("%d", &m);
printf("请输入0-1之间的t\n");
scanf("%lf", &t);
srand((unsigned)time(NULL));
int iterNum = 0;
int index=0;
for (int i = 0; i < maxLength;)
{
if (i + m >= maxLength)
iterNum = maxLength - i;
else
iterNum = m;
for (int j =0;j同上。
int isInNodes (int n)
{
int i;
for (i = 0; i < 3; i++)
{
if (nodes[i].data == access[n])
{
return 1;
}
}
return 0;
}
页面是否已经在链表中。
LNode* isinLinks (int n)
{
LNode*p, *q;
p = idle.next;
q = NULL;
while (p)
{
if (p->data == access[n])
{
if (q != NULL)
{
q->next = p->next;
p->next = NULL;
idle.num--;
break;
}
else
{
idle.next = NULL;
}
}
q = p;
p = p->next;
}
if (p == NULL)
{
p = modified.next;
while (p != NULL)
{
if (p->data == access[n])
{
if (p == modified.next)
{ modified.next = p->next; }
else
{
q->next = p->next;
p->next = NULL;
modified.num--;
}
if (modified.num == 0)
{ modified.next = NULL; }
break;
}
q = p;
p = p->next;
}
}
return p;
}
void PBA (int n)
{
if (isInNodes (n))
{
printf ("已装入内存\n");
}
else
if (index == size)
{
LNode *p;
if ( (p = isinLinks (n)) != NULL)
{
nodes = (LNode*) realloc (nodes, (size + 1) * sizeof (LNode));
nodes[size] .data = p->data;
nodes[size].flag = p->flag;
nodes[size].modify = p->modify;
nodes[size].next = p->next;
free (p);
size++;
index++;
}
else
{
lost++;//缺页
if (nodes[n % 3].modify == 1)
{
addToLink (nodes[n % 3].data, 1);
}
else
{
addToLink (nodes[n % 3].data, 0);
}
nodes[n % 3].data = access[n];
nodes[n % 3].flag = 1;
nodes[n % 3].next = NULL;
if (rand() % 10 < 4)
{
nodes[n % 3].modify = 0;
}
else
{
nodes[n % 3].modify = 1;
}
}
}
else
{
nodes[index].data = access[n];
nodes[index].flag = 1;
nodes[index].next = NULL;
if (rand() % 10 < 4)
{
nodes[index].modify = 1;
}
else
{
nodes[index].modify = 0;
}
index++;
}
}
PBA算法实现函数。
void addToLink (int data, int type)
{
LNode* p;
LNode* q;
q = (LNode*) malloc (sizeof (LNode));
q->data = data;
q->flag = 1;
if (type == 1)
{
q->modify = 1;
p = modified.next;
}
else
{
q->modify = 0;
p = idle.next;
}
q->next = NULL;
if (p == NULL)
{
if (type == 0)
{
idle.next = q;
}
else
{
modified.next = q;
}
}
else
{
while (p)
{
if (p->next == NULL)
{
p->next = q;
break;
}
else
{
p = p->next;
}
}
}
if (type == 0)
{
idle.num += 1;
if (idle.num == 10)
{
emptyIdle();
}
}
else
{
modified.num += 1;
if (modified.num == 10)
{
emptyModi();
}
}
}
页面添加到已修改页面链表和空闲链表上。
void emptyIdle ()
{
LNode* p;
p = idle.next;
while (p)
{
idle.next = p->next;
free (p);
p = idle.next;
}
idle.num = 0;
}
将空闲链表上的所有页面送出内存。
void emptyModi()
{
LNode* p;
p = modified.next;
while (p)
{
modified.next = p->next;
free (p);
p = modified.next;
}
modified.num = 0;
}
将已修改页面链表上所有的链表送出内存。
int main()
{
int i = 0, j = 0;
generate();
printf ("页面缓冲置换算法(PBA)\n");
idle.num = 0;
idle.next = NULL;
modified.num = 0;
modified.next = NULL;
nodes = (LNode*) malloc (size * sizeof (LNode));
for (i = 0; i < size; i++)
{
nodes[i].data = -1;
nodes[i].flag = 0;
nodes[i].modify = 0;
nodes[i].next = NULL;
}
for (i = 0; i < 32; i++)
{
PBA (i);
for (j = 0; j < size; j++)
{
printf ("%d ", nodes[j].data);
}
printf ("\n");
}
printf ("页面缓冲置换算法(PBA)缺页率:%f %d\n", lost / 32.0, lost);
system("pause");
return 0;
}
程序入口。
六、程序执行结果
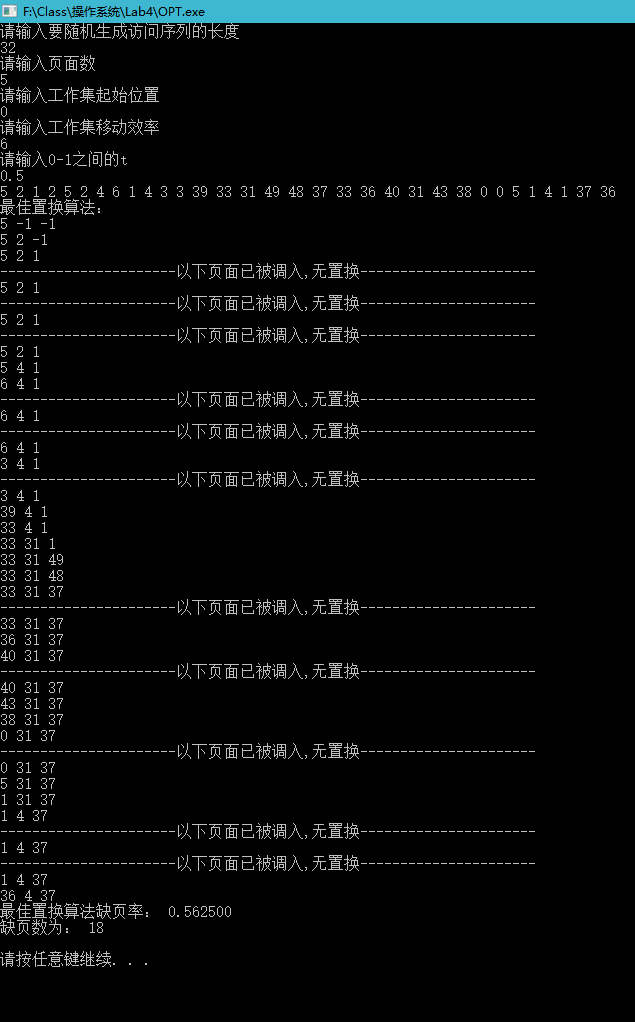
1.最佳置换算法
可以看到,一共32个页面,有18个缺页,缺页率为0.563。
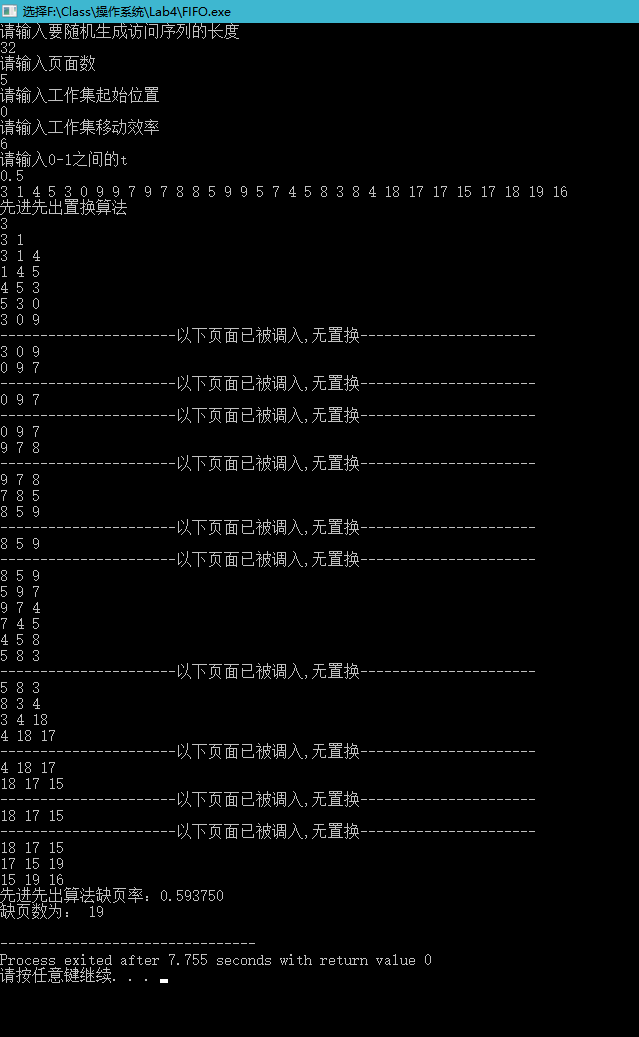
2.先进先出算法
可以看到,一共32个页面,有19个缺页,缺页率为0.594。
3.最近最久未使用置换算法
可以看到,一共32个页面,有18个缺页,缺页率为0.563。
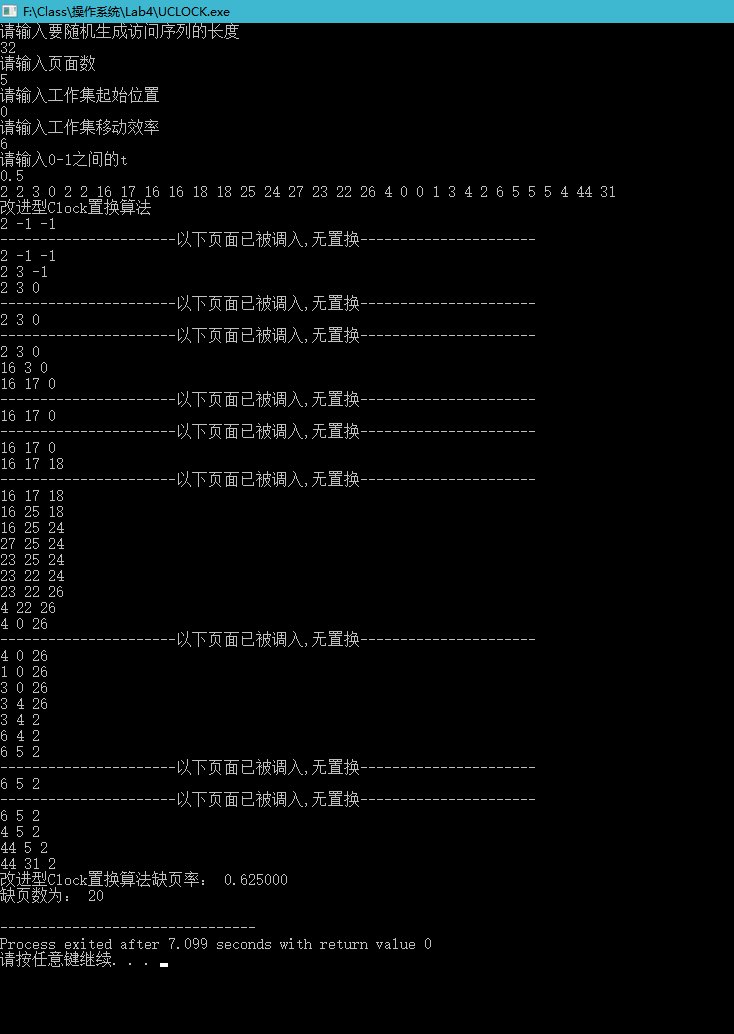
4.改进型clock置换算法
可以看到,一共32个页面,有20个缺页,缺页率为0.625。
5.页面缓冲置换算法
可以看到,一共32个页面,有18个缺页,缺页率为0.563。
七、测试与分析
利用genenrate()函数生成3个访问序列,记录每个序列下,每种算法的缺页情况,最终整理得到如下统计表格:
访问序列的长度始终为32,默认初始分配给每种算法的内存空间块数为3。
| 置换算法 | 最佳置换算法 | 先进先出置换算法 | 最近最久未使用算法 | 改进型clock置换算法 | 页面缓冲置换算法 |
|---|---|---|---|---|---|
| 测试序列1缺页数 | 13 | 17 | 20 | 15 | 18 |
| 测试序列1缺页数 | 11 | 12 | 15 | 21 | 14 |
| 测试序列1缺页数 | 14 | 16 | 16 | 16 | 14 |
使用同样的访问序列,改变分配给每种算法的的内存空间块数为5,得到实验结果如下:
| 置换算法 | 最佳置换算法 | 先进先出置换算法 | 最近最久未使用算法 | 改进型clock置换算法 | 页面缓冲置换算法 |
|---|---|---|---|---|---|
| 测试序列1缺页数 | 8 | 12 | 13 | 14 | 16 |
| 测试序列1缺页数 | 7 | 9 | 11 | 15 | 10 |
| 测试序列1缺页数 | 9 | 9 | 11 | 13 | 10 |
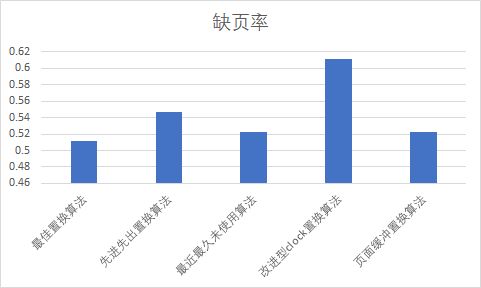
重新生成1000组序列,求缺页率平均值,可以做出以下图像:
从以上数据观察我们可以得到如下结论:
(1)同一种算法,对于不同的访问序列,其缺页率是不同,会有所变化。
(2)总的来看,最佳置换算法的缺页率是最低的,这一点是毋庸置疑的。剩下的集中算法中,页面缓冲算法的缺页率要低于其他置换算法。改进型clock算法稍微好于先进先出算法和最近最久未使用算法。先进先出算法和最近最久未使用算法性能相近。总的来看,性能(缺页率)如下。
最佳置换算法>页面缓冲置换算法>改进型clock置换算法>最近最久未使用算法>=先进先出置换算法。
(3)对比内存块数为3和内存块数为5两种情况下的同一序列下的情况,可以发现,算法的缺页率还跟分配的内存块数有关系,分配的内存块数越多,缺页率越低。这与直观感受是一致的,即导入内存的块数越多,发生缺页的可能性就越小。
八、总结
在这里对常见的三种算法做一个对比和总结:
- 先入先出法(FIFO)
最简单的页面置换算法是先入先出(FIFO)法。这种算法的实质是,总是选择在主存中停留时间最长(即最老)的一页置换,即先进入内存的页,先退出内存。理由是:最早调入内存的页,其不再被使用的可能性比刚调入内存的可能性大。建立一个FIFO队列,收容所有在内存中的页。被置换页面总是在队列头上进行。当一个页面被放入内存时,就把它插在队尾上。
这种算法只是在按线性顺序访问地址空间时才是理想的,否则效率不高。因为那些常被访问的页,往往在主存中也停留得最久,结果它们因变“老”而不得不被置换出去。
FIFO的另一个缺点是,它有一种异常现象,即在增加存储块的情况下,反而使缺页中断率增加了。当然,导致这种异常现象的页面走向实际上是很少见的。 - 最优置换算法(OPT)
最优置换(Optimal Replacement)是在理论上提出的一种算法。其实质是:当调入新的一页而必须预先置换某个老页时,所选择的老页应是将来不再被使用,或者是在最远的将来才被访问。采用这种页面置换算法,保证有最少的缺页率。
但是最优页面置换算法的实现是困难的,因为它需要人们预先就知道一个进程整个运行过程中页面走向的全部情况。不过,这个算法可用来衡量(如通过模拟实验分析或理论分析)其他算法的优劣。 - 最久未使用算法(LRU)
FIFO算法和OPT算法之间的主要差别是,FIFO算法利用页面进入内存后的时间长短作为置换依据,而OPT算法的依据是将来使用页面的时间。如果以最近的过去作为不久将来的近似,那么就可以把过去最长一段时间里不曾被使用的页面置换掉。它的实质是,当需要置换一页时,选择在最近一段时间里最久没有使用过的页面予以置换。这种算法就称为最久未使用算法(Least Recently Used,LRU)。
LRU算法是与每个页面最后使用的时间有关的。当必须置换一个页面时,LRU算法选择过去一段时间里最久未被使用的页面。
LRU算法是经常采用的页面置换算法,并被认为是相当好的,但是存在如何实现它的问题。LRU算法需要实际硬件的支持。其问题是怎么确定最后使用时间的顺序,对此有两种可行的办法:
(1)计数器。最简单的情况是使每个页表项对应一个使用时间字段,并给CPU增加一个逻辑时钟或计数器。每次存储访问,该时钟都加1。每当访问一个页面时,时钟寄存器的内容就被复制到相应页表项的使用时间字段中。这样我们就可以始终保留着每个页面最后访问的“时间”。在置换页面时,选择该时间值最小的页面。这样做,不仅要查页表,而且当页表改变时(因CPU调度)要维护这个页表中的时间,还要考虑到时钟值溢出的问题。
(2)栈。用一个栈保留页号。每当访问一个页面时,就把它从栈中取出放在栈顶上。这样一来,栈顶总是放有目前使用最多的页,而栈底放着目前最少使用的页。由于要从栈的中间移走一项,所以要用具有头尾指针的双向链连起来。在最坏的情况下,移走一页并把它放在栈顶上需要改动6个指针。每次修改都要有开销,但需要置换哪个页面却可直接得到,用不着查找,因为尾指针指向栈底,其中有被置换页。
因实现LRU算法必须有大量硬件支持,还需要一定的软件开销。所以实际实现的都是一种简单有效的LRU近似算法。
LRU和FIFO本质都是先进先出的思路,但LRU是针对页面的最近访问时间来进行排序,所以需要在每一次页面访问的时候动态的调整各个页面之间的先后顺序(每一个页面的最近访问时间变了);而FIFO针对页面进入内存的时间来进行排序,这个时间是固定不变的,所以页面之间的先后顺序是固定不变的。如果程序局部性,则LRU会很好。如果内存中所有页面都没有被访问过会退化为FIFO(如页面进入内存后没有被访问,最近访问时间与进入内存的时间相同)。
LRU算法性能较好,但系统开销较大;FIFO算法的系统的开销较小,但可能发生Belady现象。因此,择衷的办法就是Clock算法,在每一次页面访问时,它不必去动态调整页面在链表中的顺序,而仅仅是做一个标记,等待发生缺页中断的时候,再把它移动到链表的末尾。对于内存当中未被访问的页面,Clock算法的表现与LRU一样好,而对于那些曾经访问过的页面,它不能像LRU那样记住它们的准确访问顺序。
代码链接:Github