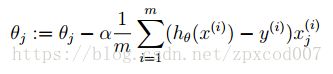多元线性回归分析-Python&SPSS
原始数据在这里
1.观察数据
首先,用Pandas打开数据,并进行观察。
import numpy
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
data = pd.read_csv('Folds5x2_pp.csv')
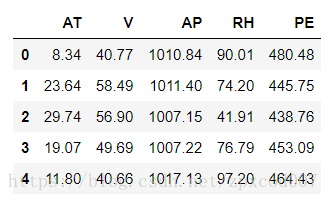
data.head() 会看到数据如下所示:
这份数据代表了一个循环发电厂,每个数据有5列,分别是:AT(温度), V(压力), AP(湿度), RH(压强), PE(输出电力)。我们不用纠结于每项具体的意思。
我们的问题是得到一个线性的关系,对应PE是样本输出,而AT/V/AP/RH这4个是样本特征, 机器学习的目的就是得到一个线性回归模型,即: PE=θ0+θ1∗AT+θ2∗V+θ3∗AP+θ4∗RH 而需要学习的,就是θ0,θ1,θ2,θ3,θ4这5个参数。
接下来对数据进行归一化处理:
data = (data - data.mean())/data.std()因为回归线的截距θ0是不受样本特征影响的,因此我们在此可以设立一个X0=1,使得回归模型为:
PE=θ0*X0+θ1∗AT+θ2∗V+θ3∗AP+θ4∗RH
将方程向量化可得:
PE = hθ(x) = θx (θ应转置)
2.线性回归
在线性回归中,首先应建立 cost function,当 cost function 的值最小时所取得θ值为所求的θ。
在线性回归中,Cost function如下所示:
因此,可以在Python中建立函数求损失方程:
def CostFunction(X,y,theta):
inner = np.power((X*theta.T)-y,2)
return np.sum(inner)/(2*len(X))然后,设初始θ为=[0,0,0,0,0],可得到最初的J(θ)值为0.49994774247491858,代码如下所示
col = data.shape[1]
X = data.iloc[:,0:col-1]
y = data.iloc[:,col-1:col]
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0,0,0,0]))
temp = np.matrix(np.zeros(theta.shape))CostFunction(X,y,theta)
接下来,有两种方法可以使用。1.梯度下降法(gradient descent)和 2.最小二乘法(normal equation)。在此我们使用梯度下降法来求解。
梯度下降法是求得J对θ的偏导数,通过设置步长,迭代使J(θ)逐步下降,从而求得局部最优解。公式如下所示:
j:特征编号
m:样本编号
我们可以在Python中写出计算迭代后的θ和J(θ)
def gradientDescent(X,y,theta,alpha,iters):
temp = np.matrix(np.zeros(theta.shape))
parameters = int(theta.ravel().shape[1])
cost = np.zeros(iters)
for i in range(iters):
error = (X*theta.T)-y
for j in range(parameters):
term = np.multiply(error,X[:,j])
temp[0,j] = theta[0,j] - (alpha/len(X))*np.sum(term)
theta = temp
cost[i] = CostFunction(X,y,theta)
return theta,cost-5.22080706e-14,-8.63485491e-01,-1.74182863e-01,2.16058120e-02,-1.35205248e-01
此时 J(θ)的值为0.0379648。
通过,可视化J(θ)和迭代次数可以发现,J(θ)收敛的非常快。
画图观察预测值和损失值,距离直线约近说明损失越小:
predicted = X*g.T
predicted = predicted.flatten().A[0]
y_f= y.flatten().A[0]fig, ax = plt.subplots()
ax.scatter(y_f,predicted)
ax.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4)
ax.set_xlabel('Measured')
ax.set_ylabel('Predicted')
plt.show()3.sckit-learn
代码如下:
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y) 0,-0.86350078,-0.17417154,0.02160293,-0.13521023
4.SPSS
在看看SPSS
同样先将数据标准化后进行线
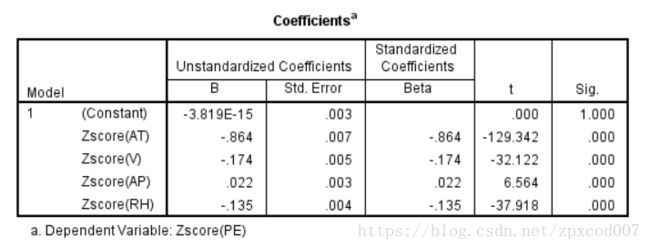
然后进行线性回归分析得到结果:
嘛…和前面两种方法的结果也差不多…就这样吧。