计算机视觉学习4_python_RANSAC_全景拼接

全景拼接原理介绍

流程
1、针对某个场景拍摄多张/序列图像
2、通过匹配特征（sift匹配）计算下一张图像与上一张图像之间的变换结构。
3、图像映射，将下一张图像叠加到上一张图像的坐标系中
4、变换后的融合/合成

重复上述过程

进行sift匹配

这里不对sift算法深入讨论，可以移步我另一个博客https://blog.csdn.net/zxm_jimin/article/details/88597258

因为在匹配时很可能会出现部分错配现象，应该采用少数服从多数，剔除掉这些少数不合适的点。

普通最小二乘法是保守派：在现有数据下，如何实现最优。是从一个整体误差最小的角度去考虑，尽量谁也不得罪。

RANSAC

RANSAC是改革派：首先假设数据具有某种特性（目的），为了达到目的，适当割舍一些现有的数据。

RANSAC是“RANdom SAmple Consensus”（随机一致性采样）的缩写，它于1981年由Fischler和Bolles最先提出。该方法是用来找到正确模型来拟合带有噪声数据的迭代方法。给定一个模型，例如点集之间 的单应性矩阵，RANSAC 基本的思想是，数据中包含正确的点和噪声点，合理的模型应该能够在描述正确数据点的同时摒弃噪声点。

由于一张图片中像素点数量大，采用最小二乘法运算量大，计算速度慢，因此采用RANSAC方法。

RANSAC参考：https://www.cnblogs.com/xingshansi/p/6763668.html

ransac

def ransac(data, model, n, k, t, d, debug=False, return_all=False)

参考:http://scipy.github.io/old-wiki/pages/Cookbook/RANSAC
伪代码:http://en.wikipedia.org/w/index.php?title=RANSAC&oldid=116358182
输入:
data - 样本点
model - 假设模型:事先自己确定
n - 生成模型所需的最少样本点
k - 最大迭代次数
t - 阈值:作为判断点满足模型的条件
d - 拟合较好时,需要的样本点最少的个数,当做阈值看待
输出:
bestfit - 最优拟合解（返回nil,如果未找到）

RANSAC 求解单应性矩阵
•RANSAC loop:

1. 随机选择四对匹配特征
2. 根据DLT计算单应矩阵 H (唯一解)
3. 对所有匹配点，计算映射误差ε= ||pi’, H pi||
4. 根据误差阈值，确定inliers（例如3-5像素）
5. 针对最大inliers集合，重新计算单应矩阵 H

我们来看一下PCV是如何调用ransac方法的

def H_from_ransac(fp,tp,model,maxiter=1000,match_theshold=10):
    """ Robust estimation of homography H from point 
        correspondences using RANSAC (ransac.py from
        http://www.scipy.org/Cookbook/RANSAC).
        
        input: fp,tp (3*n arrays) points in hom. coordinates. """
    
    from PCV.tools import ransac
    
    # group corresponding points
    # 小组对应点
    data = vstack((fp,tp))
    """ 
    vstack（）：堆栈数组垂直顺序（行）
    hstack（）：堆栈数组水平顺序（列）
    concatenate（）：连接沿现有轴的数组序列
    """

    # compute H and return
    # 计算
    H,ransac_data = ransac.ransac(data.T, model, 4, maxiter, match_theshold, 10, return_all=True)
    return H,ransac_data['inliers']

我们经常使用该约束将很多图像缝补起来，拼成一个大的图像来创建全景图像。

图像配准(Apap）

图像配准是对图像进行变换，使变换后的图像能够在很好的拼接在上一张图片的坐标系。
为了能够进行图像对比和更精细的图像分析，图像配准是一步非常重要的操作。
图像配准的方法可以参考这篇博客
https://blog.csdn.net/gaoyu1253401563/article/details/80631601

我对Apap图像配准算法的一点粗浅理解

因为图片存在歪斜或两张图片的平面与平面之间景深不同（近大远小），直接将两张图片进行映射变换会导致图片中部分物体有重影现象（鬼影）。为了尽量减小这种情况，Apap算法将图片划分成小块的区域，分别在小块区域中进行图片的匹配和映射。
原理可以参考：https://blog.csdn.net/warrenwg/article/details/49759779
实现可以参考：https://blog.csdn.net/dreamguard/article/details/84898505

图像分割

参考博客 https://www.cnblogs.com/dyzll/p/5887266.html
最大流
给定指定的一个有向图，其中有两个特殊的点源S(Sources)和汇T(Sinks)，每条边有指定的容量(Capacity)，求满足条件的从S到T的最大流(MaxFlow)。
最小割
割是网络中定点的一个划分，它把网络中的所有顶点划分成两个顶点集合S和T，其中源点s∈S,汇点t∈T。记为CUT(S,T)，满足条件的从S到T的最小割（Min cut）。

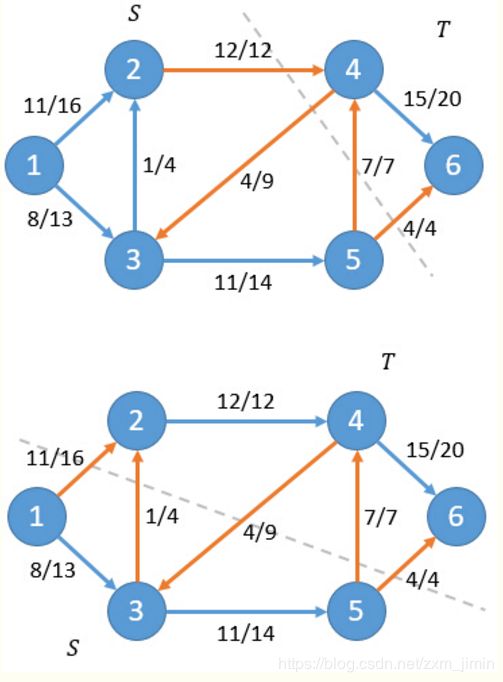
可以计算出对于这两种情况净流f(S,T)等于19。
一个直观的解释是：根据网络流的定义，只有源点s会产生流量，汇点t会接收流量。因此任意非s和t的点u，其净流量一定为0，也即是Σ(f(u,v))=0。而源点s的流量最终都会通过割(S,T)的边到达汇点t，所以网络流的流f等于割的静流f(S,T)。

对于一个网络流图G=(V,E)，其中有源点s和汇点t，那么下面三个条件是等价的：

1. 流f是图G的最大流
2. 残留网络Gf不存在增广路
3. 对于G的某一个割(S,T)，此时f = C(S,T)

找到最小割后，沿最小割进行分割，可以得到比较好的效果。

其他人的效果:

变换后的融合/合成（multi-band blending与alpha blending）

warp.py的panorama方法
基本思想：创建一个很大的图像，图像中全部填充为0，使其与中心图像平行，再将所有的图像扭曲到上面。
采用alpha blending方法

def panorama(H,fromim,toim,padding=2400,delta=2400):
    """ 通过混合两个图像创建水平全景
         使用单应性H（优选使用RANSAC估计）。
         结果是与toim具有相同高度的图像。
          '填充'指定填充像素数和“delta”附加转换。 """ 
    
    # check if images are grayscale or color
    is_color = len(fromim.shape) == 3
    
    # homography transformation for geometric_transform()
    def transf(p):
        p2 = dot(H,[p[0],p[1],1])
        return (p2[0]/p2[2],p2[1]/p2[2])
    
    if H[1,2]<0: # fromim is to the right
        print('warp - right')
        # transform fromim
        if is_color:
            # pad the destination image with zeros to the right
            toim_t = hstack((toim,zeros((toim.shape[0],padding,3))))
            fromim_t = zeros((toim.shape[0],toim.shape[1]+padding,toim.shape[2]))
            for col in range(3):
                fromim_t[:,:,col] = ndimage.geometric_transform(fromim[:,:,col],
                                        transf,(toim.shape[0],toim.shape[1]+padding))
        else:
            # pad the destination image with zeros to the right
            toim_t = hstack((toim,zeros((toim.shape[0],padding))))
            fromim_t = ndimage.geometric_transform(fromim,transf,
                                    (toim.shape[0],toim.shape[1]+padding)) 
    else:
        print('warp - left')
        # add translation to compensate for padding to the left
        H_delta = array([[1,0,0],[0,1,-delta],[0,0,1]])
        H = dot(H,H_delta)
        # transform fromim
        if is_color:
            # pad the destination image with zeros to the left
            toim_t = hstack((zeros((toim.shape[0],padding,3)),toim))
            fromim_t = zeros((toim.shape[0],toim.shape[1]+padding,toim.shape[2]))
            for col in range(3):
                fromim_t[:,:,col] = ndimage.geometric_transform(fromim[:,:,col],
                                            transf,(toim.shape[0],toim.shape[1]+padding))
        else:
            # pad the destination image with zeros to the left
            toim_t = hstack((zeros((toim.shape[0],padding)),toim))
            fromim_t = ndimage.geometric_transform(fromim,
                                    transf,(toim.shape[0],toim.shape[1]+padding))
    
    # blend and return (put fromim above toim)
    if is_color:
        # all non black pixels
        alpha = ((fromim_t[:,:,0] * fromim_t[:,:,1] * fromim_t[:,:,2] ) > 0)
        for col in range(3):
            toim_t[:,:,col] = fromim_t[:,:,col]*alpha + toim_t[:,:,col]*(1-alpha)
    else:
        alpha = (fromim_t > 0) #求出的映射区域找出
        toim_t = fromim_t*alpha + toim_t*(1-alpha)
        # 做加法运算 点对点相加 alpha来确定是否处于变换范围内 做叠加操作
    
    return toim_t

算法思路：
先判断目前图片是位于上一张图片的左边还是右边
然后利用alpha通道，将两幅图像融合
alpha=1 当前图片完全不透明 得到前景（即当前图片）
alpha=0 当前图片完全透明得到黑色预设背景

图片是集美大学的中山纪念馆

采用上面算法匹配后，出现这种分割很明显的图片，十分不自然。
我们看到匹配后的图片融合程度不是很好，因为算法并未考虑全局拼接多张图片平均亮度的问题。

multi-band blending是目前图像融和方面比较好的方法
原理：
1.建立两幅图像的拉普拉斯金字塔
2.求高斯金字塔（掩模金字塔-为了拼接左右两幅图像）因为其具有尺度不变性
3. 进行拼接blendLapPyrs() ; 在每一层上将左右laplacian图像直接拼起来得结果金字塔resultLapPyr
4.重建图像: 从最高层结果图
将左右laplacian图像拼成的resultLapPyr金字塔中每一层，从上到下插值放大并和下一层相加，即得blend图像结果（reconstructImgFromLapPyramid）

且我们可以将拉普拉斯金字塔理解为高斯金字塔的逆形式。

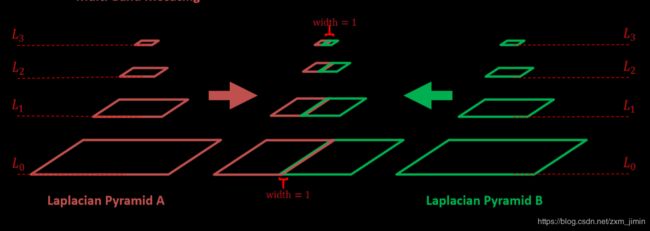
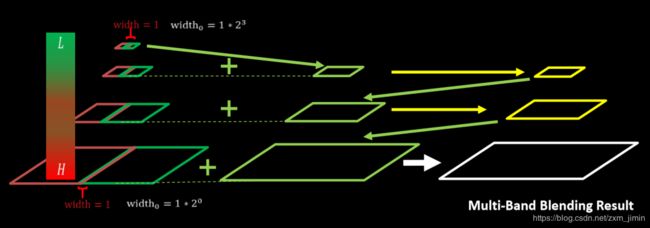
原理可以参考：
https://blog.csdn.net/abcjennifer/article/details/7628655
https://blog.csdn.net/xbcreal/article/details/52629465

本文使用的stitch方法中也使用与multi-band blending相似的方法

image stitch(国外开源的图像拼接)

这里原理可以参考：https://blog.csdn.net/yangpan011/article/details/81387299
实现参考：https://github.com/kushalvyas/Python-Multiple-Image-Stitching

实现拼接效果：

代码实现

from pylab import *
from numpy import *
from PIL import Image

# If you have PCV installed, these imports should work
from PCV.geometry import homography, warp
from PCV.localdescriptors import sift

"""
This is the panorama example from section 3.3.
"""

# set paths to data folder

featname = ['../mydata/jmu_match/jmu' + str(i + 1) + '.sift' for i in range(5)]
imname = ['../mydata/jmu_match/jmu' + str(i + 1) + '.jpg' for i in range(5)]

# extract features and match
l = {}
d = {}
for i in range(5):
    sift.process_image(imname[i], featname[i])
    l[i], d[i] = sift.read_features_from_file(featname[i])

matches = {}
for i in range(4):
    matches[i] = sift.match(d[i + 1], d[i])

# visualize the matches (Figure 3-11 in the book)
# sift匹配可视化
for i in range(4):
    im1 = array(Image.open(imname[i]))
    im2 = array(Image.open(imname[i + 1]))
    figure()
    sift.plot_matches(im2, im1, l[i + 1], l[i], matches[i], show_below=True)


# function to convert the matches to hom. points
# 将匹配转换成齐次坐标点的函数
def convert_points(j):
    ndx = matches[j].nonzero()[0]
    fp = homography.make_homog(l[j + 1][ndx, :2].T)
    ndx2 = [int(matches[j][i]) for i in ndx]
    tp = homography.make_homog(l[j][ndx2, :2].T)

    # switch x and y - TODO this should move elsewhere
    fp = vstack([fp[1], fp[0], fp[2]])
    tp = vstack([tp[1], tp[0], tp[2]])
    return fp, tp


# estimate the homographies
# 估计单应性矩阵
model = homography.RansacModel()

fp, tp = convert_points(1)
H_12 = homography.H_from_ransac(fp, tp, model)[0]  # im 1 to 2  # im1 到 im2 的单应性矩阵


fp, tp = convert_points(0)
H_01 = homography.H_from_ransac(fp, tp, model)[0]  # im 0 to 1

tp, fp = convert_points(2)  # NB: reverse order
H_32 = homography.H_from_ransac(fp, tp, model)[0]  # im 3 to 2

tp, fp = convert_points(3)  # NB: reverse order
H_43 = homography.H_from_ransac(fp, tp, model)[0]  # im 4 to 3

# warp the images
# 扭曲图像

delta = 2000  # for padding and translation 用于填充和平移

im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12, im1, im2, delta, delta)

im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12, H_01), im1, im_12, delta, delta)

im1 = array(Image.open(imname[3]), "f")
im_32 = warp.panorama(H_32, im1, im_02, delta, delta)

im1 = array(Image.open(imname[4]), "f")
im_42 = warp.panorama(dot(H_32, H_43), im1, im_32, delta, 2 * delta)
imsave('jmu2.jpg', array(im_42, "uint8"))
figure()
imshow(array(im_42, "uint8"))
axis('off')
show()

（针对不同场景做全景拼接）

case1:景深小

分析：
1、角度没取好
3、拍摄时曝光不均导致画面分割明显

stitch优化效果：

case2：景深大

分析：
1、照片部分歪斜
2、分割不明显，融合程度好

case3：室内


室内图片拼接在最后两张中出现问题。
分析：
1、分割明显
2、照片歪斜严重
3、物体变形严重

原因分析：
1、因为建筑物相似
2、角度没取好
3、最后两张没有明显的匹配标志物

如有错误欢迎指正~