【机器学习】11:支持向量机原理1:基础原理
一、回顾:逻辑回归
在逻辑回归原理里,损失 c o s t cost cost与 x x x的关系如下:
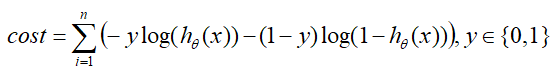
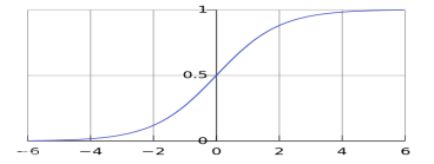
在结合下左图Sigmod函数分析可得:
- 在 y = 1 y=1 y=1是正例的情况下, c o s t ( y = 1 ) = − l o g ( h θ ( x ) ) cost(y=1)=-log(h_θ(x)) cost(y=1)=−log(hθ(x)), x x x越大, c o s t cost cost越小;
- 在 y = 0 y=0 y=0是负例的情况下, c o s t ( y = 0 ) = − l o g ( 1 − h θ ( x ) ) cost(y=0)=-log(1-h_θ(x)) cost(y=0)=−log(1−hθ(x)), x x x越小, c o s t cost cost越小;
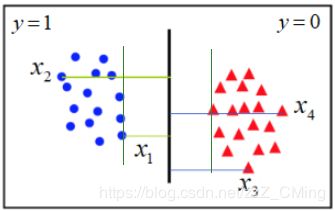
从上右图解释就是:逻辑回归在分类的过程中,会考虑每个样本点到分割线的距离——离分割线越远的点,其提供的损失 c o s t cost cost越小,而总体的损失是等于每个样本点提供的损失之和;换言之:逻辑回归是考虑整体/全局的损失,每个样本都对分割线的参数构成影响;
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
二、支持向量机介绍:
而支持向量机,它就只考虑支持向量点的损失,支持向量以外的点(也叫超越几何间隔的点)的损失规定为0,不对总体损失构成影响;
例如下图:中间的黑实线相当于分割线,左右与之平行的两条虚线构成中间的几何间隔,两条虚线上的样本点就是支持向量点,几何间隔外的样本点的损失 c o s t = 0 cost=0 cost=0;

支持向量机是一种二分类模型,其基本模型定义为特征空间上的间隔最大化的线性分类器;其学习策略便是使分割面的间隔最大;
–-----------------------------------------------------------------------------—------------------------
2.1、线性可分数据、线性不可分数据:
其数据也大多分成两类:
- 线性可分的数据,线性可分的数据使用超平面类型的边界
- 线性不可分的数据,线性不可分的数据使用超曲面类型边界;
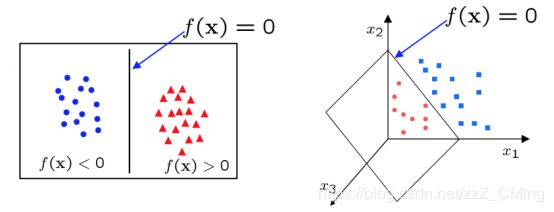
对于来自两类的一组数据能用一个线性函数正确分类的,称是线性可分的数据。线性函数可以是低维上的直线,也可以是高维上的平面,例如下图即为线性可分数据:

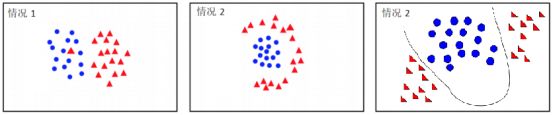
而线性不可分的数据大致有两种情况导致的:
- 样本的本质是线性可分的,但由于部分噪声的影响,导致线性不可分,这种情况的解决方法是:使用软间隔;
- 样本的本质就是线性不可分的,这种情况的解决方法是:使用核函数,将线性不可分的数据转化成线性可分的数据;
例如下图即为线性不可分数据:
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
三、支持向量机原理:
我们怎样才能确定出一个最优的划分直线/超平面 f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b呢?也就是说怎样通过训练数据学习到最优的 w w w与 b b b?
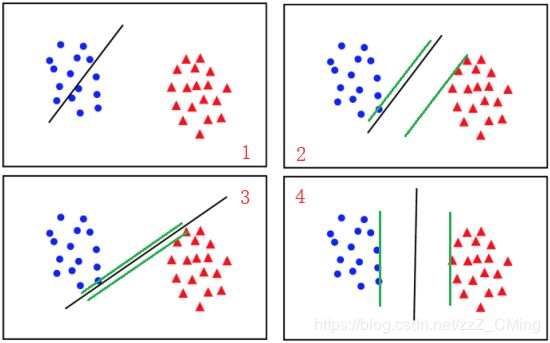
根据支持向量机的学习目标:要使分割面的间隔达到最大。从下图可以发现:1图的分割方式不能起到分类的效果,2、3的分类面间隔没有4的大;所以支持向量机就是在寻找最大间隔的分割线;
而分割线 w T x + b = 0 w^Tx+b=0 wTx+b=0中的 w w w与 b b b只和支持向量点有关,也就是说最大间距也是和支持向量点有关;
–-----------------------------------------------------------------------------—------------------------
3.1、定义中间间隔:
我们以下图 y = − 1 y=-1 y=−1(负例)中的两条绿色直线 L 1 L1 L1、 L 2 L2 L2为例,方程各为 w T x + b = L 1 w^Tx+b=L_1 wTx+b=L1, w T x + b = L 2 w^Tx+b=L_2 wTx+b=L2;根据几何原理数值上有 L 1 > L 2 L_1>L_2 L1>L2,再乘以其标签 y = − 1 y=-1 y=−1,则 y L 1 < y L 2 yL_1<yL_2 yL1<yL2,可得到的结论是—— y L i yL_i yLi越大,说明偏离中心的距离越远;
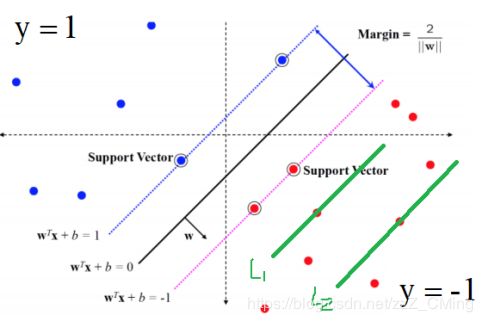
于是我们将中间间隔 D D D定义为如下:( D D D等于上图 M a r g i n Margin Margin的一半)
- D = y ( w T x + b ) = y f ( x ) D=y(w^Tx+b)=yf(x) D=y(wTx+b)=yf(x), y ∈ y \in y∈ {-1,1}
其中 w T x + b = f ( x ) w^Tx+b=f(x) wTx+b=f(x)是直线方程, x x x是任意样本点坐标, y y y是坐标所对应的标签(二维平面可简单理解为:样本标签 ∗ y *y ∗y轴截距)
有了上面这个中间间隔 D D D的定义,我们就可以将支持向量点、非支持向量点分开考虑,以便更好的确定出支持向量机的算法原理。
–-----------------------------------------------------------------------------—------------------------
3.2、考虑支持向量点到分割线的距离关系
支持向量点会确定出分割线的参数。假设已知支持向量点确定出来的分割线方程就为 f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b,则支持向量点 X = ( x 1 , x 2 , . . . ) X=(x_1,x_2,...) X=(x1,x2,...)到分割线的垂直距离 L L L为:
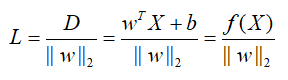
∣ ∣ w ∣ ∣ 2 ||w||_2 ∣∣w∣∣2是该分割线方程的 L − 2 L-2 L−2范数,上公式其实就是范数形式的点到直线的距离公式;
–-----------------------------------------------------------------------------—------------------------
3.3、考虑其他样本点到分割线的距离关系
根据上面中间间隔 D D D的定义,其他样本点 X = ( x 1 , x 2 , . . . ) X=(x_1,x_2,...) X=(x1,x2,...)到分割线的距离都会满足: y ( i ) ( w T x ( i ) + b ) ≥ D y^{(i)}(w^Tx^{(i)}+b)≥D y(i)(wTx(i)+b)≥D
–-----------------------------------------------------------------------------—------------------------
3.4、SVM的优化策略:(重要)
根据上面3.2、3.3提及的距离关系,支持向量机的优化策略就是:
- 在每一个样本点都满足 y ( i ) ( w T x ( i ) + b ) ≥ D y^{(i)}(w^Tx^{(i)}+b)≥D y(i)(wTx(i)+b)≥D的前提下,使支持向量点到分割线的垂直距离 L L L最大化。
数学表达式即可定义为下左式:
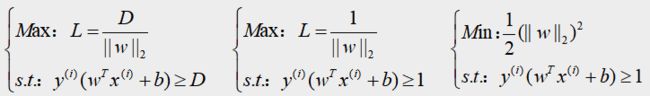
上左式需要转化,计算转化的过程如下:
- 由于 D D D是一个不小于0的系数,所以——在目标函数中不对 L L L的变化构成影响,可以去掉;在约束函数中 D D D也可作为分母除进左式进行系数缩放,于是就变成上中式;
- 分割线方程的L-2范数也是一个不小于0的系数,所以——求目标函数的最大值也相当于求目标函数倒数的最小值( “ 1 / 2 ” “1/2” “1/2”和 “ 平 方 ” “平方” “平方”的操作是方便后面求导),于是最终式就变成上右式:
于是之前的支持向量机的优化问题就转化为一个普通的凸优化问题,得到的上右式。
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
四、支持向量机求解:(重要)
总括:支持向量机的求解过程一共可分为四步:
- 定义最大间隔,得到支持向量机的数学表达式(上面第三部分最后得到的式子);
- 用拉格朗日乘子法转化数学表达式;
- 对偶问题处理;
- SMO优化算法(序列最小最优化算法)求解 w w w、 b b b,得到超平面方程。
我们在第三部分最后得到的数学表达式的基础上,详细介绍2、3、4步是如何实现的;
–-----------------------------------------------------------------------------—------------------------
4.1、拉格朗日乘子法
拉格朗日乘子法的主要思想:是引入新参数 (即拉格朗日乘子),将约束条件函数与目标原函数联系到一起,使能配成与变量数量相等的等式方程,从而求出得到目标原函数极值的各个变量的解。定义如下:

所以根据以上定义,经过转化后得到的拉格朗日乘子式即为:
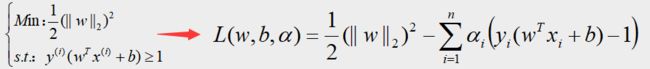
注意:上图的拉格朗日乘子式 L ( w , b , α ) L(w,b,α) L(w,b,α)的自变量分别是 w w w、 b b b、 α α α
研究可以发现,由于样本集任意一点都会满足约束条件: y i ( w T x i + b ) − 1 y_i(w^Tx_i+b)-1 yi(wTxi+b)−1的值大于等于0,加上 α > 0 α>0 α>0,所以上面得到的拉格朗日乘子式的减数是一个不小于0的值,所以 L ( w , b , α ) L(w,b,α) L(w,b,α)是存在最大值的,且最大值就等于:
- m a x L ( w , b , α ) = maxL(w,b,α)= maxL(w,b,α)= 1 2 1 \over 2 21 ( ∣ ∣ w ∣ ∣ 2 ) 2 (||w||_2)^2 (∣∣w∣∣2)2,
而我们的目标是求 m i n ( min( min( 1 2 1 \over 2 21 ( ∣ ∣ w ∣ ∣ 2 ) 2 ) (||w||_2)^2) (∣∣w∣∣2)2),也就是说需要将上等式左右取 m i n min min,即求取: m i n m a x L ( w , b , α ) minmaxL(w,b,α) minmaxL(w,b,α)
–-----------------------------------------------------------------------------—------------------------
4.2、对偶问题研究
上面的 p ∗ 、 d ∗ p^*、d^* p∗、d∗就是互为对偶。在对偶问题中,一般有 p ∗ ≥ d ∗ p^*≥d^* p∗≥d∗,当在满足KKT条件时有: p ∗ = d ∗ p^*=d^* p∗=d∗;
(补充知识:有同学会问:为什么非要做一次对偶问题研究呢?简单说就是:使数据降维,方便计算;具体原因可以详见这里)
现在我们求解的目标就由求解 p ∗ p^* p∗转成求解 d ∗ = m a x m i n L ( w , b , α ) d^*=maxminL(w,b,α) d∗=maxminL(w,b,α)了,拆分后就是先求 m i n min min再求 m a x max max;
–-----------------------------------------------------------------------------—------------------------
第一步:求解 m i n L ( w , b , α ) minL(w,b,α) minL(w,b,α),其中自变量是 w w w和 b b b, α α α是常数
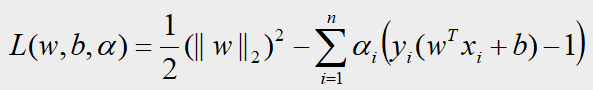
要求解 L L L关于 w w w和 b b b的最小值,我们需要对 w , b w,b w,b求偏导令其等于零,得到:
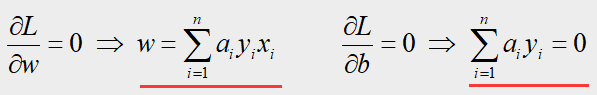
将这两个偏导结果带回上 L ( w , b , α ) L(w,b,α) L(w,b,α)式中,得到:
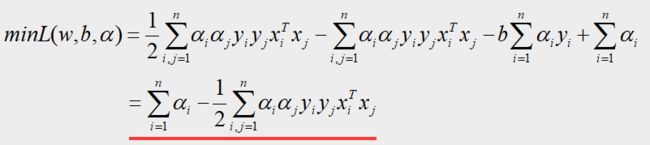
–-----------------------------------------------------------------------------—------------------------
第二步:求解 m a x m i n L ( w , b , α ) maxminL(w,b,α) maxminL(w,b,α),其中自变量是 α α α, x , y x,y x,y是常数
根据第一步的结果,问题就转化为如下规划问题:
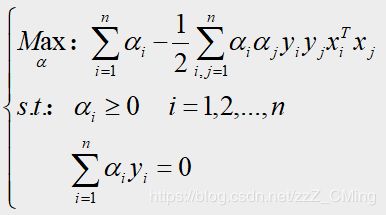
现在我们需要求以 α α α为自变量的极大值,即是关于对偶变量的优化问题,由凸二次规划的性质就能保证最优的向量 α α α是存在的;
–-----------------------------------------------------------------------------—------------------------
4.3、SMO优化算法(序列最小最优化算法)
这个算法就不在这里展开说明了,有兴趣的同学自己去了解吧,要讲起来太复杂了,本篇篇幅已经够长了
根据SMO优化算法:
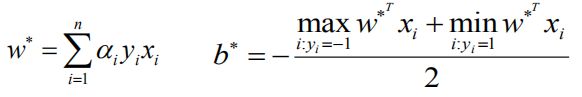
- α α α是4.2解出来的最优解,
- y i y_i yi是 i i i点的类别标签,1或者-1,
- x i x_i xi是 i i i点的坐标数据,矩阵式;
根据上面公式就可求出 w w w和 b b b,即最优超平面的参数;
–-----------------------------------------------------------------------------—------------------------
以上便是SVM的主要算法过程,下面附带一个例子加深了解
–-----------------------------------------------------------------------------—------------------------
4.4、举例
例:我们有三个训练数据,正例点 x 1 = ( 3 , 3 ) T x_1=(3,3)^T x1=(3,3)T, x 2 = ( 4 , 3 ) T x_2=(4,3)^T x2=(4,3)T,负例点 x 3 = ( 1 , 1 ) T x_3=(1,1)^T x3=(1,1)T,试求最大间隔的超平面方程。
解:设超平面的方程为: w T x + b = 0 w^Tx+b=0 wTx+b=0,因为这是个二维求解,所以 w w w的维度等于2,所以更一般的超平面方程的表达式为:
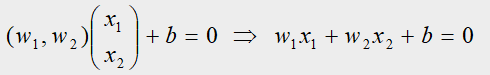
根据3.4介绍,再带入正例、负例的坐标得到的数学规划表达式如下:

再根据4.2第二步介绍,转化后的规划问题即为:
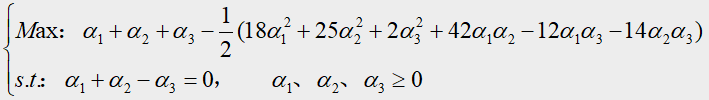
(注释:解释上面 M a x Max Max式子是如何通过4.2第二步得到的——在本章节最后有补充)
将 α 1 + α 2 = α 3 α_1+α_2=α_3 α1+α2=α3带入上面的目标函数,得到只关于 α 1 α_1 α1、 α 2 α_2 α2的函数:
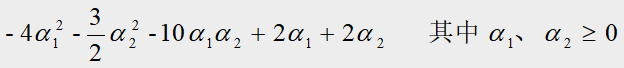
我们需要求上式的最大值,所以对 α 1 α_1 α1求偏导令其偏导等于零,即: − 8 α 1 − 10 α 2 + 2 = 0 -8α_1-10α_2+2=0 −8α1−10α2+2=0,
由于在约束条件 α 1 、 α 2 、 α 3 ≥ 0 α_1、α_2、α_3≥0 α1、α2、α3≥0的情况下有 α 1 + α 2 = α 3 α_1+α_2=α_3 α1+α2=α3,所以上式只有两组解:要么 α 1 = 0 α_1=0 α1=0,要么 α 2 = 0 α_2=0 α2=0;
将这两组解回代到拉格朗日乘子式可以发现: α 1 = 0 α_1=0 α1=0的值要小于 α 2 = 0 α_2=0 α2=0的值,所以上式的最优解为: α 2 = 0 α_2=0 α2=0, α 1 = α 3 = α_1=α_3= α1=α3= 1 4 1 \over4 41;
将最优解带入4.3介绍的SMO优化算法中得到: w 1 = w 2 = w_1=w_2= w1=w2= 1 2 1 \over2 21, b = − 2 b=-2 b=−2;( w = α 1 y 1 x 1 + α 2 y 2 x 2 + α 3 y 3 x 3 w=α_1y_1x_1+α_2y_2x_2+α_3y_3x_3 w=α1y1x1+α2y2x2+α3y3x3)
所以最大间隔的超平面方程为: 1 2 1\over2 21 x 1 x_1 x1+ 1 2 1\over2 21 x 2 x_2 x2-2=0,支持向量为 x 1 、 x 3 x_1、x_3 x1、x3
–-----------------------------------------------------------------------------—------------------------
补充: M a x Max Max式子是如何通过4.2第二步得到?——以 42 α 1 α 2 42α_1α_2 42α1α2为例:
在4.2第二步, M a x Max Max式子的减数部分为如下, x x x是对应的样本点坐标, y y y是样本点对应的标签;
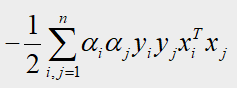
42 α 1 α 2 42α_1α_2 42α1α2来自于两部分: i = 1 , j = 2 i=1,j=2 i=1,j=2和 i = 2 , j = 1 i=2,j=1 i=2,j=1,
看 i = 1 , j = 2 i=1,j=2 i=1,j=2部分: ( i = 2 , j = 1 i=2,j=1 i=2,j=1部分同理)
- 当 i = 1 , j = 2 i=1,j=2 i=1,j=2,上式即为: α 1 α 2 y 1 y 2 x 1 T x 2 α_1α_2y_1y_2x^T_1x_2 α1α2y1y2x1Tx2。
- y 1 = 1 y_1=1 y1=1、 y 2 = 1 y_2=1 y2=1, y 1 ∗ y 2 y_1*y_2 y1∗y2决定符号为正;
- x 1 = ( 3 , 3 ) T x_1=(3,3)^T x1=(3,3)T, x 2 = ( 4 , 3 ) T x_2=(4,3)^T x2=(4,3)T,矩阵相乘 x 1 T x 2 x^T_1x_2 x1Tx2= 3 ∗ 4 + 3 ∗ 3 = 21 3*4+3*3=21 3∗4+3∗3=21
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
后记:
【线性可分】的支持向量机原理大致如上,介于本篇篇幅过长,【线性不可分数据】的处理方法,例如:软间隔、核函数在我的下一篇博客:【机器学习】11:支持向量机原理2:软间隔与核函数处理方法
