常见几种java排序算法
1.插入排序
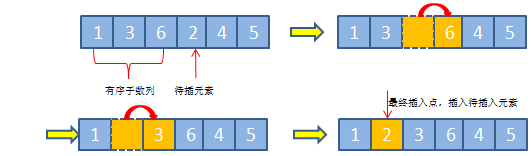
一次插入排序的操作过程:将待插元素,依次与已排序好的子数列元素从后到前进行比较,如果当前元素值比待插元素值大,则将移位到与其相邻的后一个位置,否则直接将待插元素插入当前元素相邻的后一位置,因为说明已经找到插入点的最终位置
public class InsertSort {
public static void sort(int[] arr) {
if (arr.length >= 2) {
for (int i = 1; i < arr.length; i++) {
//挖出一个要用来插入的值,同时位置上留下一个可以存新的值的坑
int x = arr[i];
int j = i - 1;
//在前面有一个或连续多个值比x大的时候,一直循环往前面找,将x插入到这串值前面
while (j >= 0 && arr[j] > x) {
//当arr[j]比x大的时候,将j向后移一位,正好填到坑中
arr[j + 1] = arr[j];
j--;
}
//将x插入到最前面
arr[j + 1] = x;
}
}
}
}
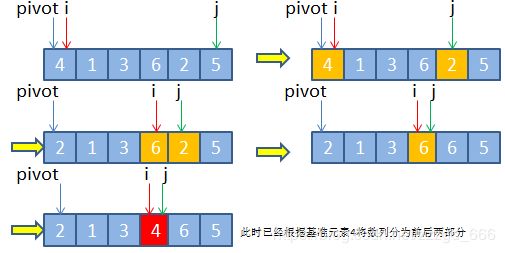
2.分治排序法,快速排序法
选择待排数列的首部第一个元素为基准元素,设置两指针,分别指向数列首尾部位置,假设两指针分别设为i和j。每次遍历的过程是这样的,首先遍历指针j所指向的元素,直到j指向的元素值小于基准元素时,停止遍历,将其与指针i所指向的元素进行交换,因为当前指针所指位置就是用于插入较基准元素小的元素,然后再将指针i加一。接着轮到指针i遍历,直到i所指向的元素值大于基准元素时,停止遍历,将其与指针j所指向的元素进行交换,之所以可以交换,是因为指针j所指向的元素刚刚已经交换到前半部分呢,故可以直接选择覆盖就行,这样就将大于基准元素的元素放于后半部分。依此类推,直到指针i与指针相等或者大于时,停止外部循环。最后直接将基准元素直接放置于指针i所指向的位置即可,完成分区操作。
public class QuickSort {
public static void sort(int[] arr,int begin,int end) {
//先定义两个参数接收排序起始值和结束值
int a = begin;
int b = end;
//先判断a是否大于b
if (a >= b) {
//没必要排序
return;
}
//基准数,默认设置为第一个值
int x = arr[a];
//循环
while (a < b) {
//从后往前找,找到一个比基准数x小的值,赋给arr[a]
//如果a和b的逻辑正确--ax,就一直往下找,直到找到后面的值大于x
while (a < b && arr[b] >= x) {
b--;
}
//跳出循环,两种情况,一是a和b的逻辑不对了,a>=b,这时候排序结束.二是在后面找到了比x小的值
if (a < b) {
//将这时候找到的arr[b]放到最前面arr[a]
arr[a] = arr[b];
//排序的起始位置后移一位
a++;
}
//从前往后找,找到一个比基准数x大的值,放在最后面arr[b]
while (a < b && arr[a] <= x) {
a++;
}
if (a < b) {
arr[b] = arr[a];
//排序的终止位置前移一位
b--;
}
}
//跳出循环 a < b的逻辑不成立了,a==b重合了,此时将x赋值回去arr[a]
arr[a] = x;
//调用递归函数,再细分再排序
sort(arr,begin,a-1);
sort(arr,a+1,end);
}
}
3.冒泡排序 low版
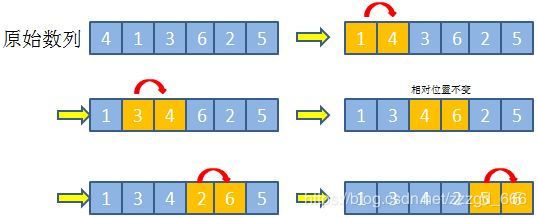
每次冒泡过程都是从数列的第一个元素开始,然后依次和剩余的元素进行比较,若小于相邻元素,则交换两者位置,同时将较大元素作为下一个比较的基准元素,继续将该元素与其相邻的元素进行比较,直到数列的最后一个元素
public class MaoPao {
public static void sort(int[] arr){
for (int i = 1; i < arr.length; i++) { //第一层for循环,用来控制冒泡的次数
for (int j = 0; j < arr.length-1; j++) { //第二层for循环,用来控制冒泡一层层到最后
//如果前一个数比后一个数大,两者调换 ,意味着泡泡向上走了一层
if (arr[j] > arr[j+1] ){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
}
4.冒泡排序 bigger版
在这个版本中,改动了两点
第一点是加入了一个布尔值,判断第二层循环中的调换有没有执行,如果没有进行两两调换,说明后面都已经排好序了,已经不需要再循环了,直接跳出循环,排序结束.
第二点是第二层循环不再循环到arr.length - 1,因为外面的i循环递增一次,说明数组最后就多了一个排好序的大泡泡.第二层循环也就不需要到最末尾一位了,可以提前结束循环
/**
* 终极版冒泡排序
* 加入一个布尔变量,如果内循环没有交换值,说明已经排序完成,提前终止
* @param arr
*/
public static void sortPlus(int[] arr){
if(arr != null && arr.length > 1){
for(int i = 0; i < arr.length - 1; i++){
// 初始化一个布尔值
boolean flag = true;
for(int j = 0; j < arr.length - i - 1 ; j++){
if(arr[j] > arr[j+1]){
// 调换
int temp;
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
// 改变flag
flag = false;
}
}
if(flag){
break;
}
}
}
}
5.选择排序
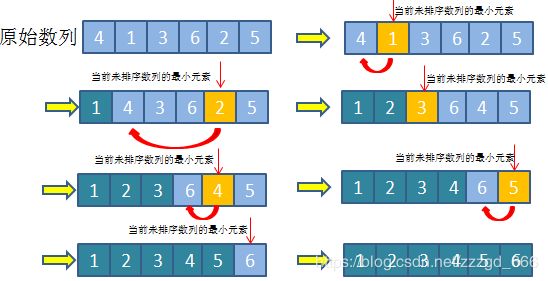
选择排序也是一种简单直观的排序算法,实现原理比较直观易懂:首先在未排序数列中找到最小元素,然后将其与数列的首部元素进行交换,然后,在剩余未排序元素中继续找出最小元素,将其与已排序数列的末尾位置元素交换。以此类推,直至所有元素圴排序完毕
public static void sort(int[] arr){
for(int i = 0; i < arr.length - 1 ; i++){
int min = i; // 遍历的区间最小的值
for (int j = i + 1; j < arr.length ;j++){
if(arr[j] < arr[min]){
// 找到当前遍历区间最小的值的索引
min = j;
}
}
if(min != i){
// 发生了调换
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}
}
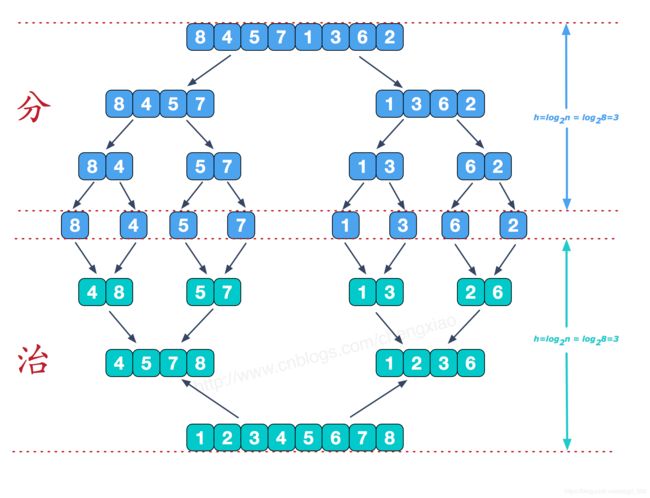
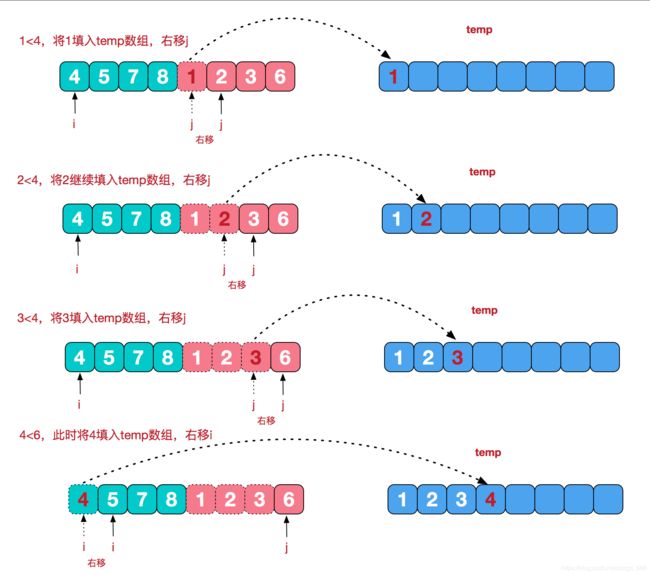
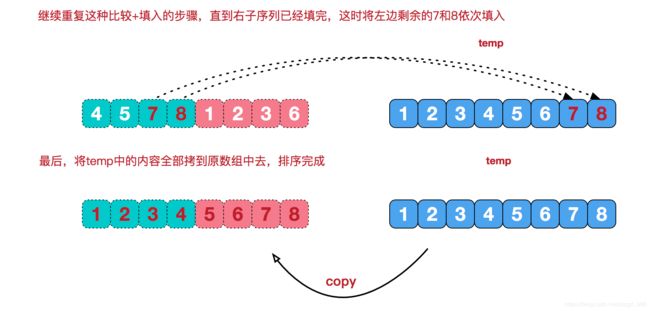
6. 归并排序
归并排序,简单的说把一串数,从中平等分为两份,再把两份再细分,直到不能细分为止,这就是分而治之的分的步骤. 再从最小的单元,两两合并,合并的规则是将其按从小到大的顺序放到一个临时数组中,再把这个临时数组替换原数组相应位置,这就是治. 图解如下:
public static void mergeSort(int[] a,int s,int e){
int m = (s + e) / 2;
if (s < e){
mergeSort(a,s,m);
mergeSort(a,m+1,e);
//归并
merge(a,s,m,e);
}
}
private static void merge(int[] a, int s, int m, int e) {
//初始化一个从起始s到终止e的一个数组
int[] temp = new int[(e - s) + 1];
//左起始指针
int l = s;
//右起始指针
int r = m+1;
int i = 0;
//将s-e这段数据在逻辑上一分为二,l-m为一个左边的数组,r-e为一个右边的数组,两边都是有序的
//从两边的第一个指针开始遍历,将其中小的那个值放在temp数组中
while (l <= m && r <= e){
if (a[l] < a[r]){
temp[i++] = a[l++];
}else{
temp[i++] = a[r++];
}
}
//将两个数组剩余的数放到temp中
while (l <= m){
temp[i++] = a[l++];
}
while (r <= e){
temp[i++] = a[r++];
}
//将temp数组覆盖原数组
for (int n = 0; n < temp.length; n++) {
a[s+n] = temp[n];
}
}
7. 其他排序
比如Arrays工具类提供的排序方法。它内部实现也是快速排序
private static void arraysSort(int[] a){
Arrays.sort(a);
}
还有就是将数组转为list,使用集合的排序方法,但是这无异于兜圈子,因为集合底层也是数组
private static void listSort(int[] a){
List<Integer> integers = Ints.asList(a);
Collections.sort(integers);
integers.toArray(new Integer[a.length]);
}
7. 比较
试了一下几个排序的速度,代码如下:
public static void main(String[] args) {
int[] arr = new int[200000];
int[] a =getRandomArr(arr);
int[] b = a.clone();
int[] c = b.clone();
int[] d = b.clone();
int[] e = b.clone();
int[] f = b.clone();
int[] g = b.clone();
int[] h = b.clone();
long s = Clock.systemDefaultZone().millis();
quickSort(a, 0, a.length - 1);
System.out.println("quickSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
mergeSort(b,0,b.length-1);
System.out.println("mergeSort: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
listSort(c);
System.out.println("listSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
arraysSort(d);
System.out.println("arraysSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
maoPaoSort(e);
System.out.println("maoPaoSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
maoPaoSortPlus(f);
System.out.println("maoPaoSortPlus耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
insertSort(g);
System.out.println("insertSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
selectSort(h);
System.out.println("selectSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
}
/**
* 获取一个打乱的数组
* @param arr
*/
private static int[] getRandomArr(int[] arr) {
for (int i = 0; i < arr.length; i++) {
arr[i] = new Random().nextInt(arr.length);
}
return arr;
}
分别对1k,1w,10w,20w大小的随机数组排序,结果如下:
得到综合结果是:
速度: 快速排序>>归并排序>>>>>插入排序>>选择排序>>冒泡排序
并且可以看到,选择排序,冒泡排序在数据量越来越大的情况下,耗时已经呈指数型上涨,而不是倍数上涨,在50w的时候已经需要足足5分钟以上
//---1k---
quickSort耗时: 0 ms
mergeSort: 1 ms
listSort耗时: 7 ms
arraysSort耗时: 1 ms
maoPaoSort耗时: 3 ms
maoPaoSortPlus耗时: 4 ms
insertSort耗时: 2 ms
selectSort耗时: 3 ms
//---1w---
quickSort耗时: 2 ms
mergeSort: 3 ms
listSort耗时: 19 ms
arraysSort耗时: 4 ms
maoPaoSort耗时: 166 ms
maoPaoSortPlus耗时: 122 ms
insertSort耗时: 12 ms
selectSort耗时: 52 ms
//---10w---
quickSort耗时: 14 ms
mergeSort: 19 ms
listSort耗时: 65 ms
arraysSort耗时: 12 ms
maoPaoSort耗时: 15242 ms
maoPaoSortPlus耗时: 15044 ms
insertSort耗时: 797 ms
selectSort耗时: 4073 ms
//---20w---
quickSort耗时: 26 ms
mergeSort: 34 ms
listSort耗时: 102 ms
arraysSort耗时: 60 ms
maoPaoSort耗时: 60811 ms
maoPaoSortPlus耗时: 60378 ms
insertSort耗时: 3279 ms
selectSort耗时: 15762 ms